5.11 Wärmeleitfähigkeit des Gitters

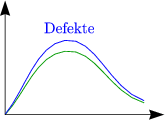
Allgemein sollte man sich folgendes Schaubild der Temperaturabhängigkeit einprägen:

Speziell für NaF gilt:

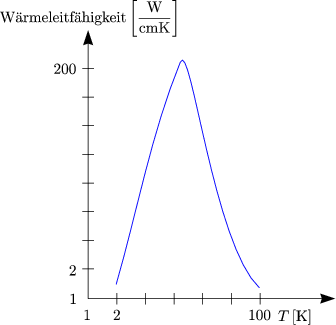
Die Ausbreitung von Phononen-Wellenpaketen und deren Streuung und Thermalisierung ist absolut nicht-trivial. ist in Metallen bei Raumtemperatur im allgemeinen größer; Rekordhalter sind aber Einkristalle aus Diamant. Die Wärmestromdichte ist:

Phononen diffundieren und stoßen, was folgende Resultate mit sich führt:

• Lokales thermisches Gleichgewicht
• Änderung des Gesamtimpulses (Widerstand)

Nach Debye werden Phononen als „Phononengas“ behandelt. Daraus ergibt sich:

C_V ist hierbei die spezifische Wärme des Phononengases, v ist die mittlere Schallgeschwindigkeit und bei l handelt es sich um die mittlere freie Weglänge, also die Weglänge, über die sich ein Phonon ausbreiten kann, bis es zum Stoß kommt. Besser wäre jedoch, wenn man die unterschiedlichen Phononenzweige separat behandeln würde. Damit wären diese drei Größen von abhängig: C_j(), v_j( und l_j(). Nach Debye gibt es einen effektiven Zweig mit v, _max = _D und C_V .

In Isolatoren gibt es verschiedene Streumechanismen infolge von Phononen und Defekten:

Der dominante Beitrag zu kommt von Phononen mit E = _q k_BT. Man spricht auch von „dominanten Phononen“; diese bestimmen daher die Temperaturabhängigkeit von .

• Phononen-Phononen-Stöße:

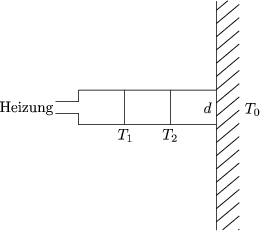
  Wichtig ist hier insbesondere der 3-Phononen-Prozeß. Dieser folgt aus dem Term 3.Ordnung in der Potentialentwicklung. Die Energie beträgt dann ₁ = ₂ = ₃. Für den Quasiimpuls gilt ₁ = ₂ = ₃ + G.

  • Erzeugung:

    

  • Vernichtung:

    

  • N-Normalprozesse: G = 0

    

    Hierbei ist der Quasiimpuls erhalten; es gibt keinen Wärmewiderstand. Dieser Prozeß ist wichtig für Thermalisierung.

  • U-Umklappprozesse: G0

    

    Hier ist der Quasiimpuls nicht erhalten. Sowohl die Impulsrichtung als auch der Energiefluß kann umgekehrt werden. Dies führt zu einem Wärmewiderstand.

  Kommen wir nun zur Temperaturabhängigkeit.

  • Hohe Temperatur: T >

    Für T > gilt für alle Phononen ~ _D. Alles sind damit U-Prozesse und l^-1 ist proportional zur Zahl der thermischen Phononen und damit proportional zu T. Damit ist .

  • Mittlere Temperatur: T <

    Die U-Prozesse sterben langsam aus mit abnehmender Temperatur, wenn die dominanten Phononen eine Energie k_BT < haben. Damit erhalten wir eine exponentielle Temperaturabhängigkeit, nämlich T exp (?).

  • Kleine Temperatur: T «

    Geht gegen unendlich? Hier findet eine Streuung an Defekten und der Oberfläche statt. Die Oberfläche des Materials wird dann wichtig, wenn l d. Damit ist also C_V ^. d T^{3 .} d.

    

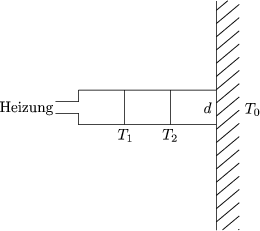
    hängt damit von der Geometrie des Material ab. Den Bereich, in dem die Leitfähigkeit proportional zu T³ ist, nennt man Casimir-Bereich. Beispielsweise gilt für die Querschnitte von LiF etwa 1 × 1 bis 7 × 7mm². Des weiteren ist die Rauhigkeit der Oberfläche wichtig aufgrund der Berücksichtigung spiegelnder und diffuser Streuung.

• Punktdefekte:

  Hier sind zwei Prozesse zu berücksichtigen:

  • Resonante Wechselwirkung bei Defekten mit der Anregungsenergie E_D

    Damit ist bei T ~ reduziert aufgrund der dominanten Phononen.

  • Rayleighstreuung l^{-1 4} T⁴

    Diese ist effektiv bei hohen Temperaturen. Aber bei hohen T dominiert die Phonon-Phonon- Wechselwirkung mit U-Prozessen, welche beobachtbar bei _max ist.