5.10 Anharmonische Eigenschaften des Gitters

Sonst hätte man keine Wechselwirkung der Phononen untereinander. Diese würden unendlich lange leben.

Es bestünde kein thermisches Gleichgewicht und man hätte eine unendlich große Wärmeleitfähigkeit.
Es gäbe keine thermische Expansion.
Die elastischen Konstante wären unabhängig von T und p.

Im Prinzip kann man den Term 3.Ordnung in der Potentialentwicklung berücksichtigen. Damit erhält man die sogenannte 3-Phononen-Präzession. Da die gewöhnliche Rechnung schnell übersichtlich wird, wollen wir an dieser Stelle nur eine gemittelte, pauschale Diskussion durchführen. Betrachten wir die thermische Expansion:

Der Erwartungswert <x> befindet sich gerade in der Mitte des Potentials unabhängig von der Besetzung, das heißt unabhängig von der Temperatur.

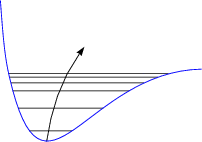
<x> hängt von der Besetzung, also von der Temperatur T ab. Es gibt damit eine kleine thermische Ausdehnung. Dies gilt beispielsweise für Invar (Fe_0,65Ni_0,35). (Invar wurde 1886 entdeckt, während man versuchte, Munitionseigenschaften der Artillerie zu verbessern.) Die Ursache dafür sind elektronische Effekte, welche Gittereffekte kompensieren. Ein anderes Beispiel ist Zerodur, welches für Kochfelder verwendet wird. Für die thermische Expansion wollen wir nun eine phänomenologische Betrachtung nach GRÜNEISEN durchführen, um eine Verknüpfung zwischen Kompressibilität und spezifischer Wärme zu finden. Die freie Energie eines harmonischen Oszillators kann beschrieben werden durch folgenden Zusammenhang:

( ( )) -hw- 1 FHO = -kBT lnZ = kBT ln 1 - exp - kBT + 2hw

Z ist hierbei die Zustandssumme (siehe Theorie F):

sum ( ) Z = exp - -Ei- i kBT

Im Festkörper liegen Phononen (Eigenmoden) mit dem Wellenvektor q und dem Zweig i vor. Dann muß des weiteren ein Term addiert werden, welche die elastische Energie beschreibt, also V = V - V ₀.

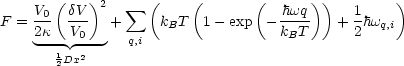
( )2 ( ( ( )) ) F = V0- dV- + sum kBT 1- exp - hwq- + 1hwq,i 2k--V0-- q,i kBT 2 1Dx2 2

Den Druck erhält man nun durch Betrachtung von F = U - TS. Dieses kann auch als totales Differential geschrieben werden:

dF = dU -T dS- SdT = dQ - pdV- T dS-S dT = T dS-p dV- T dS-S dT = -p dV- SdT

Damit folgt dann:

|-----------------------| |(dF ) @E | | dV- = - p <==> p = - @V| ------T------------------

( ) sum ( ) p = -1- dV- - h @wq,i- ----(-1-)----+ 1 k V0 q,i @V exp hkwBT- - 1 2

ist des Pudels Kern. Dieser ist gleich Null im harmonischen Fall. Als starke Vereinfachung betrachten wir nun die Grüneisenannahme. Diese besagt, daß die relative Frequenzänderung sich ergibt aus:

dw- dV- w = -g V

bezeichnet man als Grüneisen-Parameter. Differentiell gilt:

@(ln(w)) g = --------- @(ln(V ))

Es handelt sich um einen mittleren Wert für alle Zweige, welcher unabhängig von ist. Meist liegt in der Größenordnung von 1 bis 2, womit gilt -.

( ) sum ( ) p = - 1 dV- + g- hwq,i ---(1---)-+ 1 k V V q,i exp hkBwT-- 2 ----------- ----------- U

Die Zustandsgleichung lautet damit:

dV- pV = - k + gU (T)

( ) ( ) d-- ==> @p- = gCV- oc gCV dT V @T V V

Es handelt sich um die Druckänderung mit T bei „eingeklemmter“ Probe. Wir rechnen dies um in einen linearen thermischen Ausdehnungskoeffizienten. Dazu definieren wir:

1( dl) 1 (@V ) a = - --- = --- --- l dT p 3V @p T

Mit der Kompressibilität = -_T und mit _V_p_T = -1 erhalten wir:

( ) @p- 3a- @T V = k

Daraus erhalten wir schlußendlich die Grüneisenbeziehung:

|---------------| |a = gkCV- oc C | ------3V------V-|

ist in etwa temperaturunabhängig. Bei hohen Temperaturen gilt ~ const. (Dulong-Petit) und bei tiefen Temperaturen ~ T³ (Debyesche Näherung). Wir mißt man experimentell?

Druckabhängigkeit von Schallgeschwindigkeit (Brillouin-, Raman-, inelastische Neutronenstreuung)
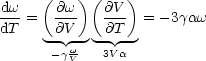
Temperaturabhängigkeit der Phononenfrequenzen (siehe Raman an Si) $( ) ( ) dw-= @w- @V- = - 3gaw dT -@V-- @T -- -gwV- 3Va$
ist konstant bei hohen Temperaturen T. Damit gilt d -dT.

Für amorphe Festkörper gilt:

CV = AT + BT 3

a = aT + bT3

In Quarzglas gilt a = -10^-9 und damit = -65. Dies liegt wiederum an den Tunnelsystemen.

[next] [prev] [prev-tail] [front] [up]