5.9 Spezifische Wärme amorpher Festkörper bei tiefen Temperaturen

Bei tiefen Temperaturen werden langwellige Phononen wichtig. Dies ist in Ordnung für < 400GHz 20K. Es solle also Debye’s Näherung gelten. Aber Quarzglas besitzt eine spezifische Wärme C_V T (!) für T < 1K und zwei Größenordnungen zu groß bei 0,1K. Ursache dafür sind die sogenannten „Tunnelsysteme“. Es handelt sich hierbei um „Teilchen“, Atome oder Atomgruppen, deren Natur letztlich im Detail unbekannt ist.

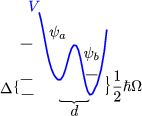
Es ist jedoch bekannt, daß sich diese Teilchen in einem Doppelmuldenpotential befinden. Sie können also in der Nachbarschaft ein zweites Potentialminimum finden. Teilchen tunneln zwischen Potentialbarriere hin und her. Dies führt zu einer niederenergetischen Anregung. Hierbei gilt:

_a und _b sind Wellenfunktionen für lokalisierte Teilchen. Beim Tunneleffekt gibt es einen Überlapp dieser beiden Wellenfunktionen. _a und _b bilden zwei neue gemeinsame Wellenfunktionen, ähnlich wie bei H₂⁺.

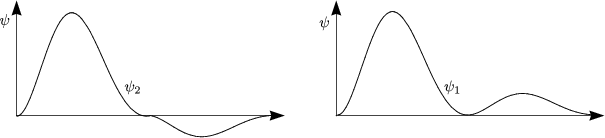
Hierbei gilt E = , wobei ₀ die Tunnelaufspaltung ist. Mittels der quantenmechanischen Störungstheorie und der WKB-Methode (Wenzel, Kramers, Brillouin) erhält man ₀ = exp(-) mit ² = . Es stellt sich jedoch die Frage, was genau hier tunnelt. Dieses ist jedoch im Detail unbekannt. Man könnte annehmen, es handelt sich um ein einziges Atom; diese Vorstellung ist jedoch naiv. Betrachtet man die gekoppelte Bewegung mehrerer Atome und berücksichtigt man außerdem, welche Parameter wichtig sind und wie sich diese verteilen, so erhält man das Tunnelmodell (phänomenologisch):

P ist hierbei eine Konstante. Dieses erlaubt die erfolgreiche Beschreibung vieler Experimente. Berechnen wir die spezifische Wärme aus der Zustandsdichte D(E) bezüglich der Energie:

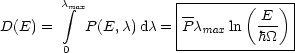
_max stellt eine Obergrenze dar, welche jedoch unbeobachtbar ist, da der Überlapp gegen Null geht. D(E) ln ist eine „langsame“ Funktion bezüglich E. Sie ist also näherungsweise konstant. Daher erhalten wir C_V T. Die Zahl dieser Tunnelsysteme in amorphen Festkörpern liegt bei 10¹⁷ .