|
-Raum, auf der die Energie konstant ist: E(
) = EF. Diese Fläche kann auch in
verschiedenen Bändern liegen; man spricht dann von den verschiedenen Zweigen der
Fermifläche. An der Brillouinzone gilt E(
) |
k|2 (siehe oben). Damit stehen die
Flächen konstanter Energie (auch Fermifläche) senkrecht auf der Zonenbegrenzung
(Bragg-Ebenen). Dies führt zu einer Deformation dieser Energieflächen und damit zu
einer Deformation der Fermifläche.
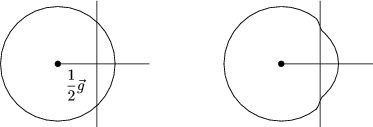
Betrachten wir beispielsweise den zweidimensionalen Fall:
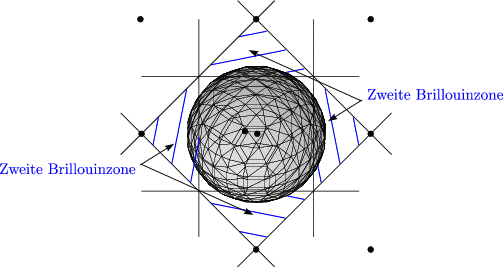
Es gibt eine schwache Permutation, falls die Fermifläche vollständig innerhalb der 1.Brillouinzone liegt.
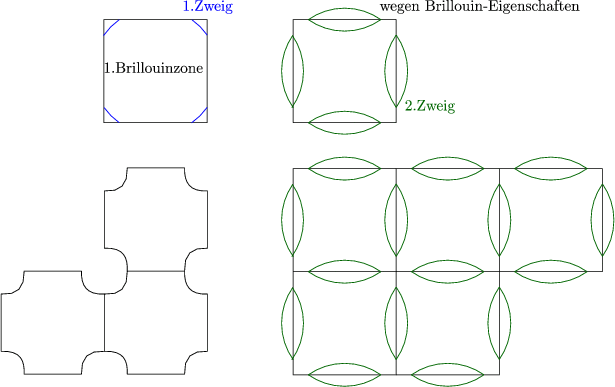
Bei Alkalimetallen (bcc) stellt man fest, daß in drei Dimensionen die Fermifläche vollständig in der 1.Brillouinzone liegt. Diese ist in der Tat so klein, daß sie mit der 1.Brillouinzone nicht in Wechselwirkung tritt. Damit ist die Fermifläche fast kugelförmig. Wenn man die Edelmetalle (Au, Ag, Cu (fcc)) anschaut, wird man feststellen, daß die d-Elektronen (+1s-Elektron) für die Fermifläche keine besondere Rolle spielen.
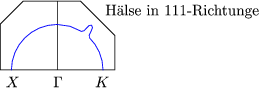
3-Valenzelektronen-Metall (fcc) beispielsweise Al (siehe ASHCROFT Seite 301)
Die Fermiflächen in Ionen sind wichtig für Transporteigenschaften (siehe unten). Wegen kT « EF bewegen sich Elektronen im allgemeinen nur auf der Fermifläche auf komischen Bahnen. Damit wird die exponentielle Bestimmung der Fermifläche mit Transport im Magnetfeld möglich (sieh unten).
Bilder: Experiment (IBACH LÜTH), Beispiel Cu: 
-Abhängigkeit über Winkelabhängigkeit