[next] [prev] [prev-tail] [tail] [up]

11.3 Makroskopische Wellenfunktion

COOPERpaare haben Spin 0, sind also Bosonen und können damit in einen gemeinsamen Zustand kondensieren mit einer makroskopischen Wellenfunktion:

y = y0exp(if(r)) = V~ nsexp(if(r))

yy* = ns beschreibt die Dichte der COOPERpaare und f(r) ist eine Phase, die über makroskopische Dimensionen wohldefiniert ist.

11.3.1 Flußquantisierung

Besitzt der Ring eine Temperatur T > Tc, so wird ein Magnetfeld angelegt. Danach wird der Ring auf T < Tc abgekühlt und das Magnetfeld ausgeschaltet. Der Fluß bleibt dann gefangen!

PIC

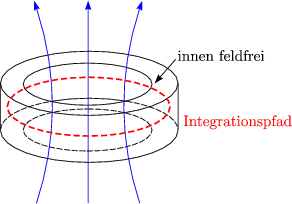
Integriert man entlang des eingezeichneten Pfades, so ergibt sich bei einem vollständigen Umlauf Df = p . 2p, wobei p eine ganze Zahl ist. Für j gilt:

------------------------------------ | hq ( ) q2 | j = -i---- y* \~/ y - y \~/ y* - --Ay*y | ------2M-------------------M--------

Im Innern des Ringes gilt j = 0. Mit q = -2e und M = 2m erhält man:

1 [h ] 0 = - m-c2 e \~/ f + 2A 0 L

Für das Umlaufintegral ergibt sich unter anderem mit dem STOKESschen Satz:

gf gf integral 0 = - h- \~/ f ds - 2 A ds = -h-.(p.2p)- 2 Bdf = - h-.(p .2p)- 2f e e e

Damit können wir den Fluß f berechnen:

|-------------| |f = p h-= pf | ------2e----0-|

f0 = h- = 2.10-15Tm2 Fluxoid 2e

[next] [prev] [prev-tail] [front] [up]