4.1 Der Vektorraum

Definition:

Die Menge $V(/= P)$ heißt reeller (komplexer Vektorraum), wenn es im Vektorraum

eine Verknüpfung +gibt derart, daß eine abelsche Gruppe ist:
- $x + y = y+ x$
- $(x+ y)+ z = x+ (y+ z)$
- $x + 0 = x$
- $x + (- x) = 0$
eine Vorschrift gibt, die jedem und jedem eindeutig ein zuordnet und die folgenden Gesetze erfüllt:
- $(ab)x = a(bx)$ mit $a$ , $b (- R$ , $x (- V$
- $a(x +y) = ax +ay$ mit $a (- R$ , $x$ , $y (- V$
- $(a+ b)x = ax + bx$ mit $a,b (- R$ , $x (- V$
- $1x = x$ für $x (- V$

Beispiele:

$F = {f|f : [0,1] '--> R}$ $f,g (- F : (f + g)(x) = f(x)+ g(x) x (- [0,1]$

$a (- R, f (- F : (af)(x) = af(x) x (- [0,1]$
$C$ ist ein reeller Vektorraum: $w, z (- C w + z (- C gen¨ugt 1.)$

$a (- R,z (- C a (- C gen¨ugt 2.)$
Vektoren sind Elemente eines Vektorraums“. $R$ (bzw. $C$ ) in der Definition von $V$ heißt Skalarbereich. Die Vorschrift unter 2.) heißt skalare Multiplikation.
$( ) q1 n q2 R = {x = ... ,qi (- R} q n$ $( ) q1 + j1 q2 + j2 n x = (qi)j)j,y = (jj)j : x +y := .. (- R . qn + jn$

$( ) ( ) 0 -q1 0 -q2 o = .. - x = .. . . 0 - qn$

$( ) aq1 n aq2 n Skalare Multiplikation: a (- R,x (- R : ax = .. (- R . aqn$

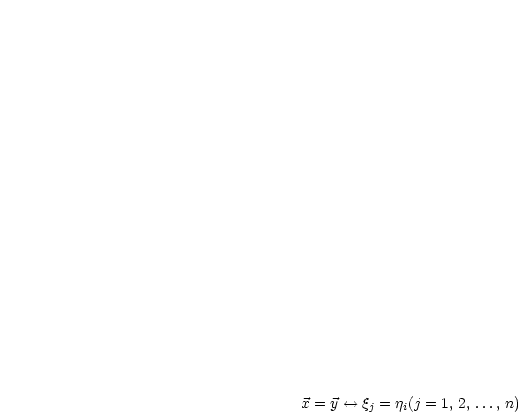
$x = y <--> qj = ji(j = 1, 2, ..., n)$

4.1.1 Geometrische Deutung ( $n = 2$ , 3)

(q1) R3 : x = q2 q3

Wähle kartesisches Koordinatensystem: Die gerichtete Strecke $OP$ ist Bild für $x$ und ebenso jede aus $x$ durch Parallelverschiebung, hervorgehende Strecke.

( ) ( ) ( ) ( ) a1 b1 b1 - a1 q1 Verschiebung von a2 nach b2 : b2 - a2 = q2 a3 b3 b3 - a3 q3

Umgekehrt sei im $R3$ eine gerichtete Strecke gegeben: Wie wird $x$ ein Tripel $( ) q1 q2 q3$ zugeordnet?

₁	= ₁ - ₁
₂	= ₂ - ₁
₃	= ₃ - ₁

$a,b$ mit gleicher oder entgegengesetzter Richtung heißen kolinear.

4.1.2 Lineare Abhängigkeit und Unabhängigkeit

Definition:

$V$ sei reeller Vektorraum. Ein Ausdruck der Form $c x + c x + ...+ c x (c (- R,x (- V ) (- V 1-1---2-2 -------n-n j j n sum cjxj j=1$ heißt Linearkombination (LK) der $x1$ , $...$ , $xn$ .

Definition:

$x1$ , $x2$ , $...$ , $xn (- V$ heißen linear unabhängig, falls aus $sum k cjxj = 0 j=1$ folgt: $c1 = c2 = ...= cn = 0$ . Sind die $x1$ , $x2$ , $...$ , $xn$ nicht linear unabhängig, so heißen sie linear abhängig, d.h. es gibt $c1$ , $...$ , $ck$ mit $sum k j=1$ $2 cj /= 0$ und $k sum cj- xj = 0 j=1$ .

Beispiel aus $R2$ :

Es ist zu zeigen, daß folgende Vektoren linear abhängig sind:

( ) ( ) ( ) 2 2 2 0 , 1 , 2

Es muß also gelten:

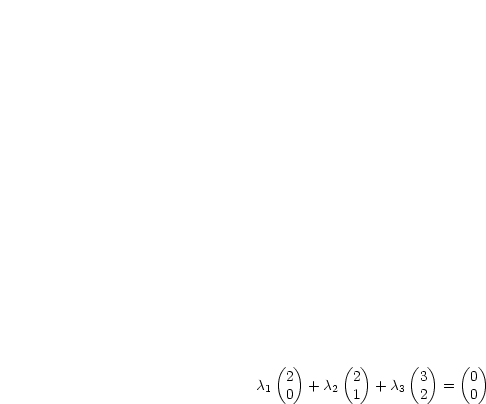
( ) ( ) ( ) ( ) c1 2 +c2 2 + c3 3 = 0 0 1 2 0

Damit erhalten wir folgendes Gleichungssystem:

( ) ( ) 2c1 + 2c2 + 3c3 = 0 + c2 + 2c3 0

2₁ + 2₂ + 3₃	= 0
+ ₂ + ₃	= 0

Damit folgt die Lösung:

c = -2c 2 3

c = 1 c 1 2 3

c3 = 1

Also sind die Vektoren linear abhängig.

Übung:

(2) (2) 0 , 1 sind linear unabh¨angig.

Sätzchen:

$a$ , $b$ sind kollinear. $<==>$ $a$ , $b$ sind linear abhängig.

$a = cb$ $<==>$ $1a+ (-c)b = o$

Beweis:

<== “c1a + c2b = o mit c1 /= 0-- > a3 = - c2b ” c1

Damit sind $a$ und $b$ kollinear.

(q1) R3 = {x = q2 ,q,q ,q (- R} q3 1 2 3

( ) ( ) q1 +j1 cq1 x = (qi),y = (yj) : x+ y = q2 +j2 ,cx = cq2 (cinR q3 +j3 cq3

a,b (- R3 kolinear: a||b <--> a,b sind linear abh¨angig. <--> a = cb

( ) ( ) b1- a1 q1 b2- a2 = q2 b3- a3 q3

Vektoren: Kraft, Geschwindigkeit, elektrisches Feld Skalare: Temperatur, Masse

4.1.3 Geraden

Gegeben sei ein Punkt $A$ in $R3$ und eine Richtung $m(/= o)$

g : x(t) = a + tm t (- R (x : R '--> R3)

Wir suchen die Parameterdarstellung der Geraden $g$ durch $A$ mit der Richtung $m$ . Dazu betrachten wir eine Gerade durch 2 Punkte $A$ und $B$ :

m = b- a

x(t) = a +t(b- a),t (- R = b+ t(b- a),t (- R

(4.1)

Beispiel:

Im Parallelogramm schneiden sich die Diagonalen in dem Punkt, der beide Diagonalen halbiert.

x = t(a+ b) = b+ t(a- b)

(t- t)a + (t- 1 + t)b = o

Da $a$ und $b$ linear unabhängig sind, ergibt sich das Gleichungssystem:

t -t = 0 t -1 + t = 0 t = t 2t = 1

1 ==> t = t =- 2

4.1.4 Ebenen

Gegeben sei ein Punkt $A$ mit $a$ und 2 Richtungen $u,v$ (linear unabhängig).

x = a+ su +tv s,t (- R = x(s,t)

(4.2)

x : R2 '--> R3

Gesucht ist die Parameterdarstellung der Ebene durch $A$ , die von $u$ und $v$ aufgespannt wird. Gegeben seien 3 Punkte $A$ , $B$ , $C$ mit den Ortsvektoren $a$ , $b$ , $c$ . ( $A$ , $B$ , $C$ liegen nicht auf einer Geraden.) $b - a$ , $c- a$ sind Vektoren (in der Ebene), welche die Ebene aufspannen.