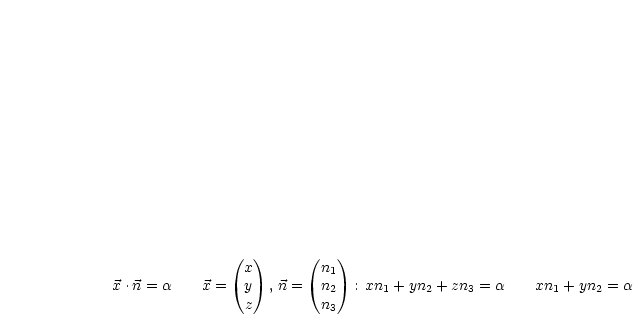(Länge/Winkel zwischen
Vektoren)
(Länge/Winkel zwischen
Vektoren) (Länge/Winkel zwischen
Vektoren)
(Länge/Winkel zwischen
Vektoren)Wähle kartesisches Koordinatensystem:

Die Länge von  (von
(von  ) - man bezeichnet diese auch als Norm von
) - man bezeichnet diese auch als Norm von  - ist
folgendermaßen definiert:
- ist
folgendermaßen definiert:

Außerdem besitzt sie folgende Eigenschaften:
 für
für 
 (
( )
)




Es sei  und
und  . Dann definiert man das Skalarprodukt (inneres
Produkt) zwischen
. Dann definiert man das Skalarprodukt (inneres
Produkt) zwischen  und
und  folgendermaßen:
folgendermaßen:

Man findet in Büchern verschiedene Bezeichnungen für das Skalarprodukt:  ,
,
![[x,y]](ma1588x.gif) ,
,  . Dieses besitzt nun folgende Eigenschaften:
. Dieses besitzt nun folgende Eigenschaften:
 für
für  ;
;  nur für
nur für 
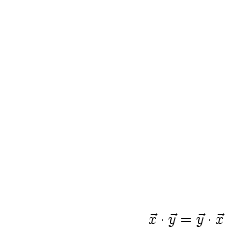
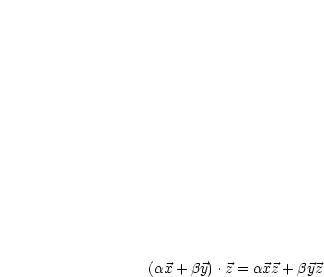 für (
für ( ,
,  ;
;  ,
,  ,
,  )
)
Die Länge der Strecke  berechnet sich durch:
berechnet sich durch:
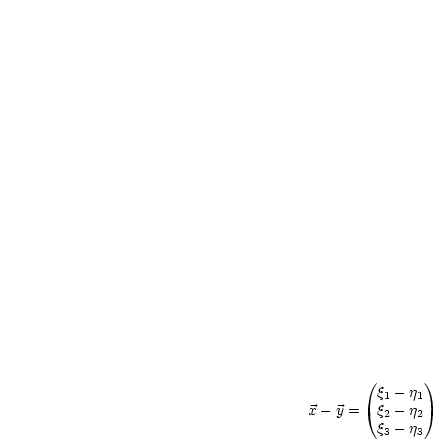

Das Skalarprodukt  läßt sich geometrisch interpretieren. Dazu betrachten wir
ein Parallelogramm mit den Seiten
läßt sich geometrisch interpretieren. Dazu betrachten wir
ein Parallelogramm mit den Seiten  und
und  .
.




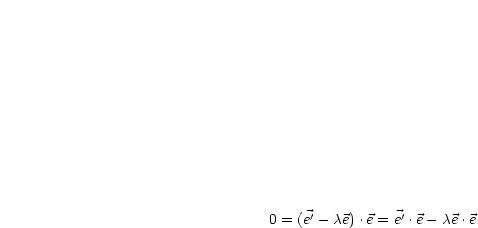



Hat  die Länge 1, so gibt
die Länge 1, so gibt  die Länge der orthogonalen Projektion von
die Länge der orthogonalen Projektion von  auf
auf
 an.
an.

|
|
Es seien  ,
,  linear abhängig.
linear abhängig.



Die drei Höhen in einem Dreieck schneiden sich in einem Punkt. Zu zeigen
ist 

 .
.  kann folgendermaßen dargestellt werden:
kann folgendermaßen dargestellt werden:

Damit ergibt sich durch Multiplikation mit  bzw.
bzw.  :
:

Wir wollen die Hesse-Normalform für Gerade  (im
(im  und Ebene
und Ebene  (im
(im
 herleiten.
herleiten.
 :
:
Wähle 

 . Daraus folgt
. Daraus folgt  für jeden
Ortsvektor von
für jeden
Ortsvektor von  .
.  ist die Hesse-Normalform für
ist die Hesse-Normalform für  (Geradengleichung), falls
(Geradengleichung), falls  und
und  von 0 zu
von 0 zu  gerichtet ist.
gerichtet ist.
 :
:
Wähle 

 und
und  . Dann ist
. Dann ist  Hesse-Normalform der Ebene.
Hesse-Normalform der Ebene.
|
|

Im kartesischen Koordinatensystem sei  gegeben.
gegeben.

Hierbei gilt  für
für  , 2, 3. Das Kroneckersymbol
, 2, 3. Das Kroneckersymbol  ist dabei
folgendermaßen definiert:
ist dabei
folgendermaßen definiert:

Aus  folgt
folgt  für
für  , 2, 3.
, 2, 3.

Für eine Ebene gilt beispielsweise: