4.3 Vektorprodukt (im <img src="msbm10-52.gif" alt="R" class="10x-x-52" />3)

4.3 Vektorprodukt (im $R3$ )

Definition:

Zwei Vektoren $a$ , $b (- R3$ wird der Vektor $p = a× b$ wie folgt zugeordnet:

$p$ $_L$ $a$ und $p$ $_L$ $b$
$f = Winkel(a,b)$ $(- [0,2p]$ , $||a × b|| = ||a||||b||sin f$
Im Falle $a ×b /= o$ bilden $a$ , $b$ , $a × b$ (in dieser Reihenfolge) ein Rechtssystem.

\text{[math]}

Auch für Anwendungen: Bwg/Haf/Wille: Höhere Mathematik für Ingenieure (5 Bände), 2. Band

4.3.1 Eigenschaften des Vektorproduktes

$a× a = o$
$a× b = -b× a$
$2 2 2 2 2 2 2 ||a× b|| = ||a|| .||b|| - ||a||||b||cos f = ||a|| ||b|| - (a .b)$
$||a× b|| =$ Flächeninhalt des von $a$ und $b$ aufgespannten Parallelogramms.
$a,b,c (- R3$ seien Rechtssystem:
Volumen dieses Parallelepipeds (Spats):
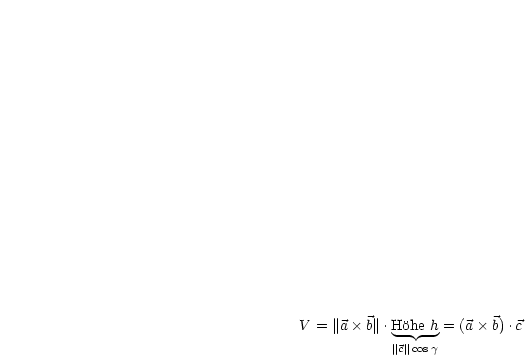
$V = ||a × b||.H¨ohe-h = (a × b) .c ||c||cosg$

3 3 a, b (- R : a ×b (- R mit

$a× b _L a,b$
$||a× b|| = ||a||.||b ||.sin f(a,b)$
$a,b,a× b bilden ein Rechtssystem.$
$||a× b|| =$ Flächeninhalt eines Parallelogramms
$(a× b).c = (b× c .a = (c× a).b$
$(a× b).c = a .(b× c) =: (a,b,c) Spatprodukt$ $(a,b,c) = (b,c,a) = (c,a,b)$

$-(b,a,c) = -(c,b,a) = -(a,c,b)$
$a,b,c$ bilden ein Rechtssystem, wenn $(a,b,c) > 0$ ist.
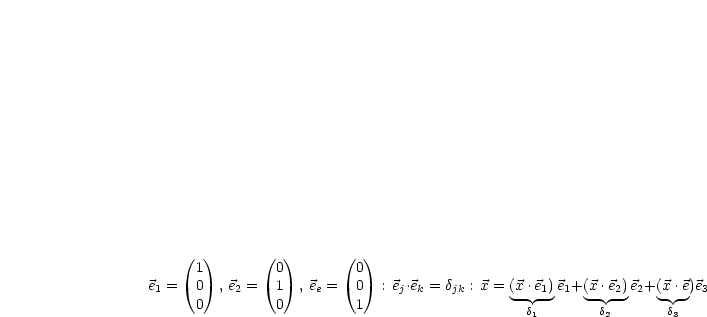
$( ) ( ) ( ) 1 0 0 e1 = 0 , e2 = 1 , ee = 0 : ej.ek = djk : x = (x-.e1)e1+(x-.e2)e2+(x.e)e3 0 0 1 d1 d2 d3$

$(e1,e2,e3) = 1$

$e1,e2,e3 und e2,e3,e1 und e3,e1,e2 bilden ein Rechtssystem.$

$e1 ×e2 = e3$

$e2 ×e3 = e1$

$e3 ×e1 = e2$

$(e1,e2,e3) = (e1× e2).e3 = e3 .e3 = 1$
Weitere Beziehungen: $} (a + b) ×c = a× c+ b ×c (ca)× b = c(a× b) = a× (cb) (c (- R) --> (ca+ gb)× c = ca × c+gb ×c$

$c(a,b,c) = (ca,b,c) = (a,cb,c) = (a,b,cc)$

$[c(a× b)].c = [(ca)× b].c$

$(a1,a2,b,b) = (a1,b,c) + (a2,b,c)$

$(a,b1 + b2,c) = (a,b1,c)+ (a,b2,c)$

$(a,b1c1 + c2) = (a,b,c1)+ (a,b,c2)$

Übung:
$a,b,c+ ca + mb = (a,b,c)+ c(a,b,a)+m(a,b,b) =0 =0$
$a,b sind linear abh¨angig <--> a× b = o$ $” --> “a = cb-- > a× b = c(a ×b) = o$

$<-- “||a× b|| = ||a||.||b ||.sin f = 0 --> f = 0,p --> a,b sind kolinear! ”$

Entwicklungssatz

a× (b× c) = (a.b).b- (a.b).c

Diese Formel nennt man auch Grassmann-Identität. Wir finden einen geometrischen Beweis auf Seite 93f im Skript. Wir benötigen:

e1 ×e2 = e3

e ×e = e 2 3 1

e3 ×e1 = e2

a× b in Koordinaten:

( 3 ) ( 3 ) 3 3 sum sum sum sum a× b = j=1ajej × bkek = (ajbkej× ek) = (ajbkej× ek) = k=1 j,k=1 j/=k = (a2b3- a3b2)e1 + (a3b1- a1b3)e2 + (a1b2- a2b1)e3 = (a1 ) (b1 ) (a2b3 - a3b2) = a2 × b2 = a3b1 - a1b3 a3 b3 a1b2 - a2b1

(4.3)

10.) Jakobi-Identität

a ×(b× c)+ b× (c× a)+ c × (a × b) = o mit 10

11.) Lagrange-Identität

(a ×b).(c× d) = a.[b×(c× d)] = a.[(b.b)c- (b.c)d] = (a.c(b.d) = (a.d)(b.c)

12.) $(a× b)× (c× d) = (a× b).dc- (a× b).cd = (a,b,d)c- (a,b,c)d$

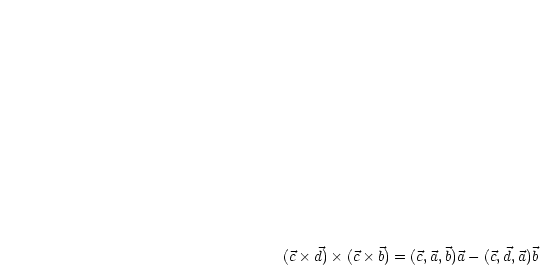
(c× d)× (c× b) = (c,a,b)a - (c,d,a)b

-(a,b,c)d+(c,d,b)a+(d,c,a)b+(a, b,d)c = 0bzw. +(a,b,c)d = (c,d,b)a+ (d,c,a)b+ (a,b,d)c= 0 a/=0 b/=0 g/=0 d/=0

Satz:

Je vier Vektoren $a$ , $b$ , $c$ , $d (- R3$ sind linear abhängig.

Beweis:

Wir können annehmen, daß je drei dieser Vektoren linear unabhängig sind.

==> a /= 0,b /= 0,g /= 0,d /= 0

b g d d = a-a+ a-b+ a-c

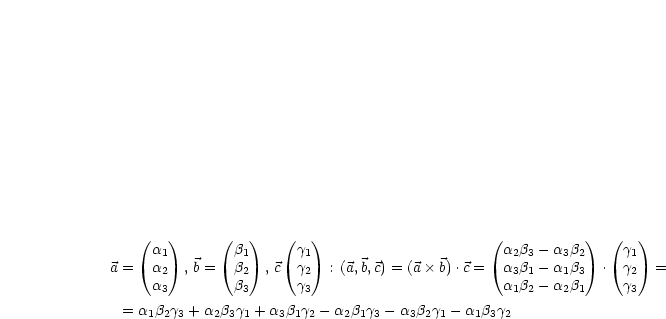( ) ( ) ( ) ( ) ( ) a1 b1 g1 a2b3- a3b2 g1 a = a2 , b = b2 , c g2 : (a,b,c) = (a× b).c = a3b1- a1b3 . g2 = a3 b3 g3 a1b2- a2b1 g3 = a1b2g3 +a2b3g1 + a3b1g2- a2b1g3- a3b2g1- a1b3g2

(4.4)

(a,b,c) = (b,c,a) = (c,a,b)

Satz:

$a$ , $b$ , $c$ sind linear abhängig. $<==>$ $(a,b,c) = 0$

Beweis $==>$ “:

2 2 2 aa + bb+ gc = o mit a + b +g > 0

|.(b × c) a(a,b,c) = 0

|.(c× a) b(b,c,a) = 0 = b(a,b,c)

|.(a× b) g(a,a,b) = 0 = g(a,b,c)

Beweis $<==$ “:

||a × b||.||c ||.cosf(a× b,c) = 0

$a× b = 0--->8 a$ , $b$ sind linear abhängig. $==>$ $a$ , $b$ , $c$ sind linear abhängig!
$c = o$ $==>$ $a$ , $b$ , $c$ sind linear abhängig!
$a× c$ $_L$ $c$ $==>$ $a$ , $b$ , $c$ liegen in einer Ebene. $==>$ $a$ , $b$ , $c$ sind linear abhängig!

Nachtrag:

n sum n=3 x .y = qjjj = ||x||||y||cosf k=1

( ) ( ) q1 j1 q2 j2 x = .. ,y = .. . . qn jn

|x.y|< ||x||||y||

SCHWARZ-Ungleichung: $||-3----|--(-n---)1(--3---)1| ||| sum qj ||< sum q2 2 sum j2 2| | j=1 j j j=1 j k=1 k | -----------------------------$
Dreiecksungleichung: $|------------------| -||x±-y||-<-||x||+-||y||-|$

Übung:

Beweis mit SCHWARZ-Ungleichung

Für $x$ , $b (- R$ und $e > 0$ läßt sich eine $e$ -Umgebung von $b$ definieren durch $|x- b|< e <--> b- e < x < b+ e$ . Gleichzeitig definieren wir für $c (- C$ , $e > 0$ eine $e$ -Umgebung von $c$ nach ${x|x- c|< e}$ . Für $x > 1$ und $n (- N$ gilt die BERNOULLI-Ungleichung $n (1 +x) > 1+ nx$ . Sind $a$ und $b > 0$ , so gibt es ein $n0 (- N$ mit $na > b$ $A$ $n > n0$ . Zu jedem $x > 0$ und $e > 0$ gibt es ein $n0 (- N$ mit $x n < e$ $A$ $n > n0$ . Für $x > 0$ , $e > 0$ gilt $x n < e$ für fast alle $n$ .

Satz:

Jede nichtleere nach oben beschränkte Menge reeller Zahlen besitzt ein Supremum.

Definition:

Fast alle natürlichen Zahlen sind alle bis auf endlich viele.

Aussage 1:
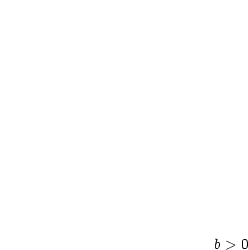Es sei $a > 1$ und $b > 0$ gegeben. Dann gilt $n a > b$ für fast alle $n$ .
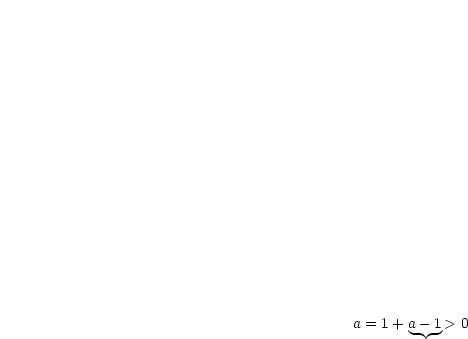
$a = 1+ a- 1 > 0$

$n n a = (1+ a--1 > 0) > 1+ n(a - 1) > n(a- 1)> b f¨ur fast alle n >0$
Aussage 2:
Es sei $e > 0$ und $0 < q < 1$ . Dann gilt $qn < e$ für fast alle $n$ .