5.1 Grenzwerte

Definition:

Eine Zahlenfolge ist eine Funktion $f$ : $N '--> C$ . Für $f(n)$ schreibt man $an$ (Folgenglieder). Anstelle von $f$ wird geschrieben: $(an)n=1,2,...$ .

$(an)$ sei reelle Zahlenfolge:

$(an)$ ist monoton wachsend $<==>$ $(an) < an+1$ $A$ $n$
$(a ) n$ ist streng monoton wachsend $<==>$ $(a ) < a n n+1$ $A$ $n$
$(an)$ ist monoton fallend $<==>$ $(an+1) < an$ $A$ $n$
$(an)$ ist streng monoton fallend $<==>$ $(an+1) < an$ $A$ $n$
$(a ) n$ heißt nach oben beschränkt, falls es ein $K (- R$ gibt mit $a < K n$ $A$ $n$
$(an)$ heißt nach unten beschränkt, falls es ein $M (- R$ gibt mit $M < an$ $A$ $n$
$(an)$ ist nicht nach oben beschränkt, falls es zu jedem $K (- R$ ein $an$ mit $K < an$ gibt.
( $...$ falls es unendlich viele $an$ mit $K < an$ gibt.
Die Zahlenfolge $(a ) n$ heißt beschränkt, falls es ein $S > 0$ gibt mit $|a |< S n$

Beispiele:

$an$ : $an = (-1)n$ $\text{[math]}$ $- 1$ , 1, $- 1$ , 1, $- 1$ , 1, $...$
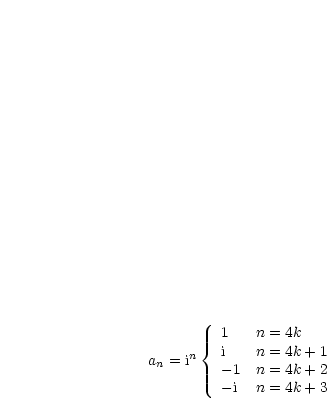$1 n = 4k { i n = 4k +1 an = in - 1 n = 4k +2 - i n = 4k +3$ für $k = 0$ , 1, $...$ ( $n = 0$ , 1, 2, $...$ )
$n an = n(- 1)$
$an = 2$ $\text{[math]}$ 2, 2, 2, $...$
$an = 1+ 1- n$
Diese Folge ist streng monoton fallend und beschränkt.
$sum n 1 an = k- j=1$
Die einzelnen Folgenglieder stellen die harmonische Reihe dar.
$3 3 1 a1 = 1, a2 = 2 , a3 = 2 + 3, ...$
$n an = 2ni$ $a1 = 1i, a2 = 1i, a3 = 3i, ... 2 2 8$
Die Folge ist beschränkt für $n > 3$ ( $2n > n$ ).
$a1 = 1$ , $an+1 = an + d$ : $a1 = 1$ , $a2 = 1+ d$ , $a3 = 1+ 2d$ : $an = 1+ (n- 1)d$ für $n = 1$ , 2, $...$
$a1 = 1$ , $an+1 = qan$ : $a1 = 1$ , $a2 = q$ , $a3 = q2$ , $...$ , $an = qn-1$ für $n = 1$ , 2, $...$
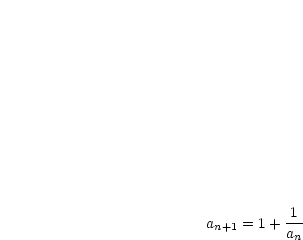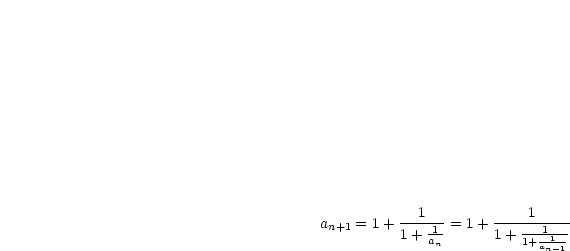
$a = 1 1$ , $a = 1 + 1-- n+1 an$ : $a = 1+ --1---= 1+ -----1---- n+1 1+ a1n 1 + 1+11-- an-1$
$a1 = 1$ , $V~ ------ an+1 = 1+ an$ : $V~ - a2 = 2$ , $V~ ---- V~ a3 = 1 + 2$ , $V~ ---- V~ --- V~ - a4 = 1 + 1+ 2$
$an = an-1 + an-2$ für $n = 3$ , 4, $...$ $a = 1, a = 1, a = 2, a = 3, a = 5, a = 8, ... 1 2 3 4 5 8$
${ 1 n = 2k -1 an = k1- -1 n = 2k k$

Definition:

Die Zahl $c (- C$ heißt Häufungspunkt (HP) der Folge $(a ) n$ , falls für jedes $e > 0| a - c| < e n$ für unendlich viele $n$ gilt.

Definition:

Eine reelle nicht nach oben (nicht nach unten) beschränkte Folge hat den uneigentlichen Häufungspunkt $+ oo$ , $(- oo )$ .

Jede reelle Zahl ist Häufungspunkt der rationalen Zahlen.

5.1.1 Satz von BOLZANO-WEIERSTRASS

Satz von BOLZANO-WEIERSTRASS (Skript Seite 121/122,Seite 142):

Jede reelle Folge besitzt einen Häufungspunkt.

Beweis:

Ist die Folge nicht beschränkt, so hat sie den Häufungspunkt $+ oo$ (oder $- oo$ ).
Es sei $(an)$ beschränkt $|an|< S A n$

Betrachte $M = {x (- R|x < an f¨ur unendlich viele n}$

$M /= P$
nach oben beschränkt

$- S (- M$
$S + 1$ ist obere Schranke von

$==>H = sup(M )$

Es sei $q (- C$ : $an = qn$ . $an$ konvergiert für $|q|< 1$ und $q = 1$ , divergiert für $|q|= 1$ (außer $q = 1$ ) und $|q|> 1$ . Betrachten wir außerdem $c (- C$ : Die Folge $an = cn$ geht gegen 0 für $n '--> oo$ .

Es gilt $limn'-->o o an = g$ , falls es zu jedem $e > 0$ ein $N (e) (- N$ derart gibt, daß aus $n > N (e)$ folgt: $|an - g|< e$ . Falls für jedes $e > 0$ $|an- g|< e$ gilt für fast alle $an$ . Konvergenz bedeutet, daß die Folge beschränkt ist und genau ein Häufungspunkt vorliegt.