5.2 Teilfolge

Es sei die Folge $(an)$ gegeben mit den Folgengliedern $a1$ , $a2$ , $a3$ , $...$ . Betrachte Folge von natürlichen Zahlen $n1$ , $n2$ , $n3$ , $...$ mit $n1 < n2 < n3 < ...$ . Es sei $bj := anj$ . Dann stellt $(bj)$ eine Teilfolge von $(an)$ dar.

Beispiele:

nj = 2j } nj = 2j -1 nj > j nj = 2j

Satz:

$(an)$ sei konvergent. $an '--> g$ $(n '--> oo )$ . Es gilt:

Jede Teilfolge konvergiert und zwar gegen $g$ . Gibt es eine divergente Teilfolge, so divergiert die Ausgangsfolge.

Die Voraussetzung besagt: Für jedes $e > 0$ gilt: $|an- g|< e$ für $n > N (e)(= n0)$ . $(ank)$ sei Teilfolge. Sei $e > 0$ : $|an- g|< e$ für $k > N$ ( $'-->$ $nk$ für $k > N$ )

Die harmonische Reihe:

Die harmonische Reihe ist divergent:

sum n 1 (sn) : sn = k k=1

Des weiteren gilt:

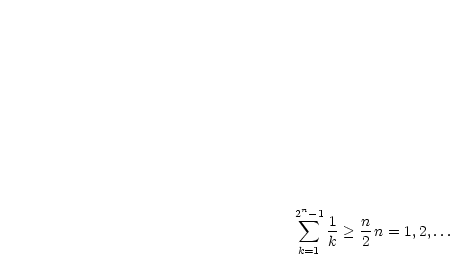
2 sum n-11 n k-> 2-n = 1,2,... k=1

Die Teilfolge $(S2n-1)$ ist unbeschränkt, divergiert also.

Satz:

Fast alle Glieder einer Teilfolge sind unendlich viele Glieder der Ausgangsfolge“. $(an)$ sei eine Folge. Ist $H$ ein Häufungspunkt von $(an)$ , so gibt es eine Teilfolge $(ank)k$ , die gegen $H$ konvergiert. Das heißt: $|an- H |< e$ für fast alle $k$ , das sind unendlich viele $(an)$ .

|an- H |< 1

n2 > n1 : an2- H |< 1 2

1 n3 > n2 : an3- H |< 3

1 an1, an2, an3, ... mit |ank - H|< k mit k = 1, 2, ...

Übung:

a '--> H(k '--> oo ) nk

Jede reelle Zahl ist Häufungspunkt rationaler Zahlen. Jede reelle Zahl ist Grenzwert rationaler Zahlen.

sum n 1 sn = k! '--> e k=1

Satz:

$(an)$ , $(bn)$ seien konvergent: $an '--> a$ $(n '--> oo )$ , $bn '--> b$ $(n '--> oo )$ . Es gelte: $an < bn$ für fast alle $n (- N$ . Dann gilt: $a < b$ .

Falsch ist: $an < bn$ für fast alle $n-- > a < b$ .

1- 1- n2 < n '--> 0

Satz:

$(an)$ , $(cn)$ seien konvergente Folgen mit demselben Grenzwert $g$ . $(bn)$ sei Folge mit $an < bn < cn$ für fast alle $n$ . Dann konvergiert $(bn)$ und es gilt $bn '--> g$ $(n '--> oo )$ .

g- e < an < g+ e,g- e < cn < g+ e f¨ur fast alle n.

g- e < a < b < c < g+ e f¨ur fast allen. n n n

Satz:

$an '--> g$ $(n '--> oo )$ und $bn '--> b$ $(n '--> oo )$ . Dann konvergieren die Folgen $(an± bn)n$ , $(can)n$ , $(anbn)bn$ , $( ) an- bn n$ $(bn /= 0,b < 0)$ $(| an|)n$ , $V~ -- ( an)n$ , $(an > 0)$ , $k (an)n$ $(k (- N)$ und zwar gegen:

$|--------------| |--------| |an± bn '--> a± b | |an|'--> |a|| --------------- ---------- |---------| V~ ----- V~ -| -can '-->-ca-| --an '-->--a-- |---------| |-------| |anbn '--> ab| ak '--> ak | ---------- -n------- |a----a-| |-n-'--> --| -bn----b-$

Beweis für $akn '--> ak$ :

akn '--> ak(n '--> oo ); k = 1,2,...

Wir führen den Beweis durch Vollständige Induktion:

Induktionsanfang:
Für $k = 1$ ist die Aussage wahr (Voraussetzung im Satz).
Induktionsschluß:
Es gilt für ein beliebiges $k > 1$ :
$k k an '--> a f¨ur n '--> oo$
- Induktionsvoraussetzung: $ak '--> ak fur n '--> oo n ¨$
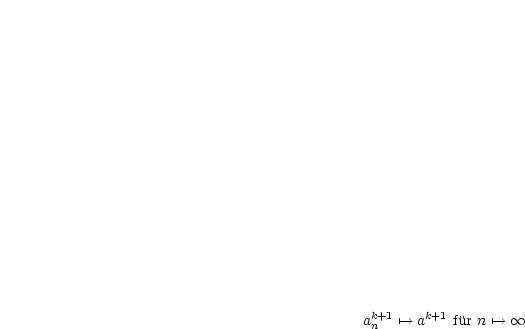
- Induktionsbehauptung: $k+1 k+1 an '--> a f¨ur n '--> oo$
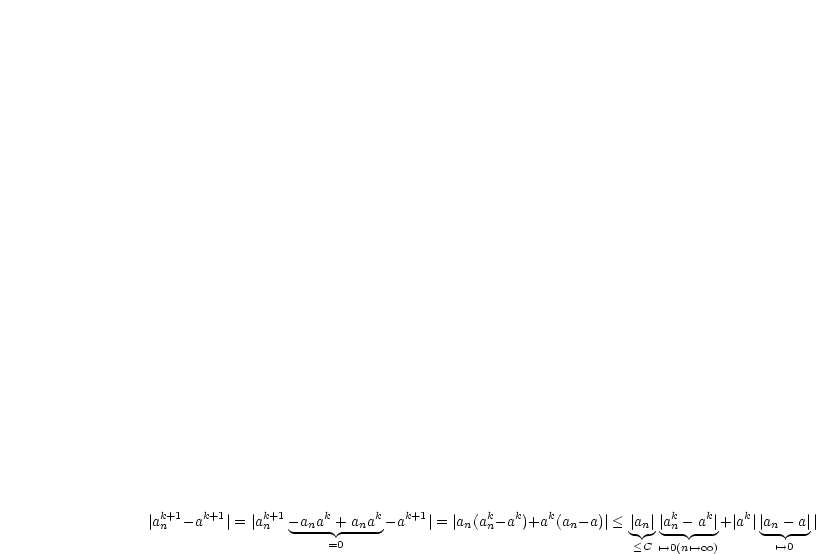
Induktionsbeweis: $k+1 k+1 k+1 k k k+1 k k k k k k |an -a |= |an --ana-+-ana-- a |= |an(an-a )+a (an- a)|< |an||an- a-|+ |a ||an---a|| =0 <C '-->0(n'-->o o ) '-->0$

Beispiele:

1.Beispiel:
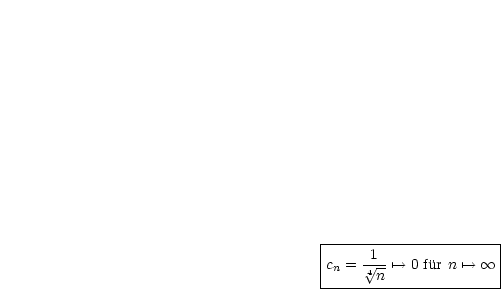
Bei den folgenden $(an)$ , $(bn)$ und $(cn)$ handelt es sich allesamt um Nullfolgen:
$|--------------------| | 1- | |an = n '--> 0 f¨ur n '--> oo ----------------------$

$|----------------------| |bn = V~ 1-'--> 0 f¨ur n '--> oo | -------n---------------|$

$|----------------------| | -1- | |cn = 4 V~ n-'--> 0 f¨ur n '--> oo | -----------------------$
2.Beispiel: $|---- V~ ------ V~ --| -an =--n+-1----n-|$
Wir verwenden zur Umformung die 3.binomische Formel und schätzen geschickt ab:
$V~ ---- V~ -- ( V~ ----- V~ -)(V ~ n-+-1-+ V~ n-) n + 1- n 1 1 0 < an = n + 1- n = n+ 1 - n V~ ------ V~ -- = V~ ------ V~ -= V~ ------ V~ --< - V~ - n+ 1 + n n + 1+ n n + 1+ n 2 n$
Damit resultiert für den Grenzwert:
$( V~ ---- V~ -) nl'-->imo o n + 1- n = 0 ”( oo - oo )“$
3.Beispiel:
Wir untersuchen die Folge $------------- |a = n- V~ n| --n----------$ auf Konvergenz. Dazu formen wir diese zunächst um und schätzen anschließend ab:
$V~ - V~ -- V~ -- V~ -- an = n - n = n(--n--1)> n >0$
Da $V~ n$ für $n '--> oo$ divergent ist, ist somit auch $(a ) n$ divergent.
4.Beispiel: $|------------| | ---n----| an = V~ n2 + n --------------$
Wir formen die Folge um und bilden den Grenzwert für $n '--> oo$ :
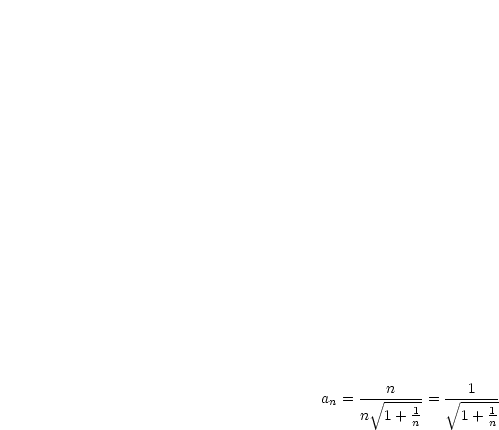
$n 1 an = - V~ ----- = V~ ----- n 1+ 1n 1+ 1n$

$1 nli'-->m oo V~ -----= 1 1 + 1n$
Damit ist $(an)$ konvergent für $n '--> oo$ und besitzt den Grenzwert 1.
5.Beispiel: Der Grenzwert folgender Folge soll berechnet werden: $|----------------| |an = (1+ (- 1)n)n| -----------------$
Hierbei muß man zwischen geradem und ungeradem $n$ unterscheiden:
- $n$ sei gerade: $2n 2n 2n 2n n a2n = (1+ (-1) ) = (1+ 1) = 2 = 4$
  
  $n nl'-->imo o a2n = nli'-->mo o 4 = oo$
  
  $|----------| limsup = oo | ------------$
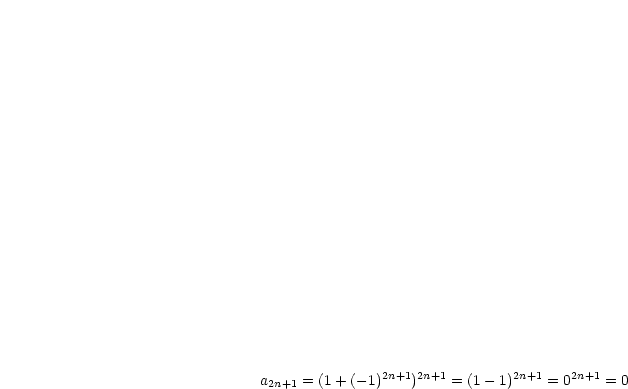
- $n$ sei ungerade: $a2n+1 = (1+ (-1)2n+1)2n+1 = (1 - 1)2n+1 = 02n+1 = 0$
  
  $|---------| lim-inf =-0-$
$|--------------| |lim inf /= lim sup| ---------------$
Daraus folgt, daß die Folge keinen Grenzwert besitzt.
6.Beispiel: Wir betrachten die Folge: $|-------(------)-| | prod n 1- | an = 1 - k2 | -----k=2----------$
Zur Berechnung des Grenzwertes nehmen wir einige Umformungen vor:
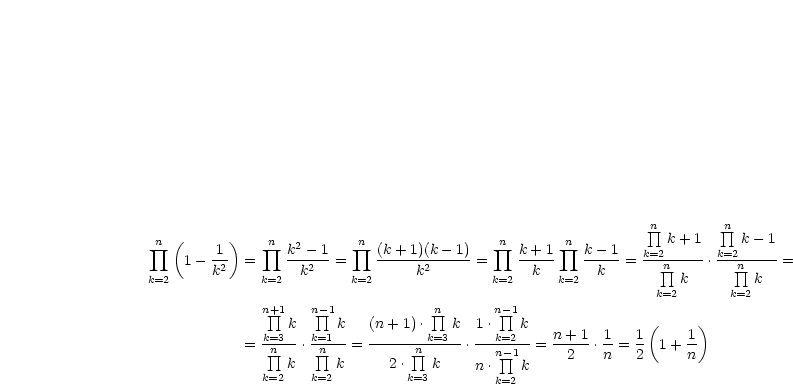$n ( ) n n n n n prod k+ 1 prod n k- 1 prod 1- 1- = prod k2--1-= prod (k+-1)(k--1) = prod k+-1- prod k--1-= k=2----- .k=2-----= k=2 k2 k=2 k2 k=2 k2 k=2 k k=2 k n prod k n prod k k=2 k=2 n prod +1 n prod -1 n prod n prod -1 k k (n+ 1) . k 1. k ( ) = k prod =n3--.k prod =n1--= ----- prod nk=3-.---kn=-21- = n-+-1.1-= 1 1+ 1- k k 2. k n . prod k 2 n 2 n k=2 k=2 k=3 k=2$ (5.1)

Nun können wir den Grenzwert berechnen:
$1 ( 1) 1 lnim'--> oo 2 1+ n = 2$
• 7.Beispiel:
Folgende Folge sei gegeben:
$|-------------------| | (n)+ (-1)n .n2| |an = -2--n-+-3---2-| --------------------$
Wir formen um:
$( ) 2 2 2 -n2-+-(--1)n-.n2- 2!(nn!-2)! +-(--1)n-.n2 n(n-2-1)-+-(--1)nn2- 1 n2(1-+-(--1)n)--n- an = n+ 3 = n + 3 = n + 3 = 2. n +3$
Nun ergibt sich für den Grenzwert:
$n 1 lim 1 .n2(1+-(-1)n)--n-= lim 1 1+-(-1)----n n'--> oo 2 n + 3 n'--> oo 2 1n + 3n2$
- $n$ sei gerade: $11 + 1- 1n 1 2 - 1n |---| ln'-->imo o 2-1+--3- = 2 1-+-3-= - oo - n n2 n n2$
- $n$ sei ungerade: $|---| lim 1 --n--= |-1 | n'--> oo 2 n+ 3 --2--$
Die beiden Häufungspunkte lauten somit:
$|----------------------| | 1 | limsup-=- oo ,-lim-inf =---2$
Da $lim sup /= lim inf$ existiert kein Grenzwert der Folge.
[prev] [prev-tail] [front] [up]

5.2 Teilfolge

Beispiele:

Satz:

Die harmonische Reihe:

Satz:

Übung:

Satz:

Satz:

Satz:

Beweis für :

Beispiele:

Beweis für $akn '--> ak$ :