


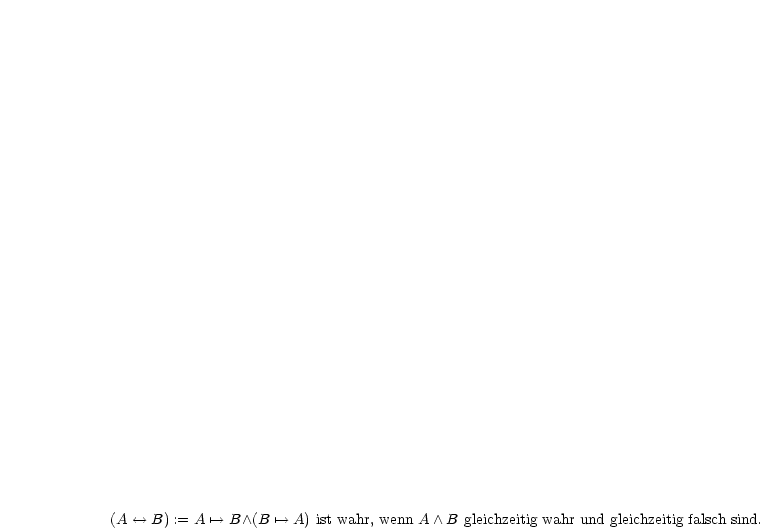
 |  |  |  |  |
| w | w | w | w | w |
| w | f | f | f | w |
| f | w | f | w | f |
| f | f | w | w | w |
Was bedeutet  ?
?

Es sei  eine natürliche Zahl. Dann gelten: eine natürliche Zahl. Dann gelten: |
1.)  ist gerade ist gerade   gerade gerade |
2.)  ist ungerade ist ungerade   ungerade ungerade |
A:  ist gerade, B:
ist gerade, B:  ist gerade
ist gerade
 , das heißt
, das heißt 
 , das heißt
, das heißt 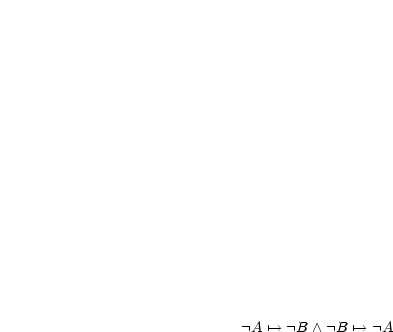

 ist nicht rational. ( ist nicht rational. ( rational: rational:  ganze Zahlen, ganze Zahlen,  ) ) |
 |  |  |  |  |  |
| w | w | w | w | w | w |
| w | f | f | f | f | w |
| f | w | w | f | f | w |
| f | f | w | f | f | w |
Die Aussage  (Voraussetzung A, Behauptung B) ist stets
wahr.
(Voraussetzung A, Behauptung B) ist stets
wahr.







 ist irrational. ist irrational. |
 ist irrational)
ist irrational)
 :
:  ist rational; es gilt also
ist rational; es gilt also  wobei
wobei  ,
,  rationale Zahlen mit ggT=1
sind. Durch Quadrieren ergibt sich:
rationale Zahlen mit ggT=1
sind. Durch Quadrieren ergibt sich:
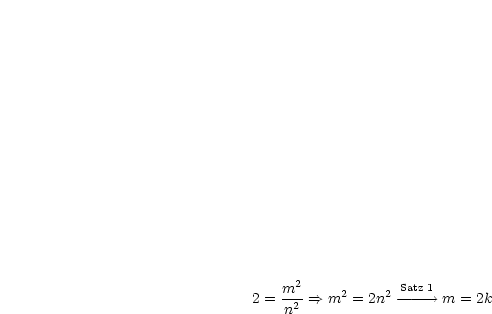
Und weiterhin folgt:

 und
und  haben daher den gemeinsamen Faktor 2, das ist aber nach
Voraussetzung falsch! Damit ist
haben daher den gemeinsamen Faktor 2, das ist aber nach
Voraussetzung falsch! Damit ist  irrational!
irrational!

