8.7 Angenherte Lsung von Gleichungen

8.7 Angenäherte Lösung von Gleichungen

g(x) = 0 <==> Fixpunktgleichung: f (x) = x

1 P(x) /= 0 : P(x)g(x)+ x = x,P(x) = --- ---f(x)--- g(x)

8.7.1 Fixpunktkriterium/Sukzessive Approximation

Satz:

$f (- C1[a,b]$ besitze die folgenden Eigenschaften:

$a < f (x) < b(x (- [a,b])$ .
Es gilt: $|f'(x)|< q < 1$ $A$ $x (- [a,b]$ , $q$ ist eine feste Zahl

Dann gelten:

Es gibt genau ein $q (- [a,b]$ mit $f (q) = q$ .
Die Folge $(xn)$ : $xn+1 = f(xn)$ , $n = 0,1,2,...$ mit beliebigem $x0 (- [a,b]$ konvergiert gegen $q$ .
Es gilt die Fehlerabschätzung: $-q--- -qn-- |q- xn| < 1- q|xn- xn-1|< 1- q| x1 - x0|$

Beweis:

Der erste Schritt ist es, den Mittelwertsatz anzuwenden. Damit ergibt sich für $x$ , $y (- [a,b]$ :

|f(x)- f(y)| = f'(q)(x - y)|< q| x -y|

|xn+1 - xn|= |f(xn) -f (xn- 1)|< q|xn- xn-1|< q2|xn-1- xn-2|

So folgt dann nach $n$ Schritten:

(xn+1 -xn) < qn(x1- x0) f¨ur n (- N

Außerdem gilt:

sum n xn+1 = x0 + (xk+1---xk) k=0 ak

Nun gilt die Abschätzung:

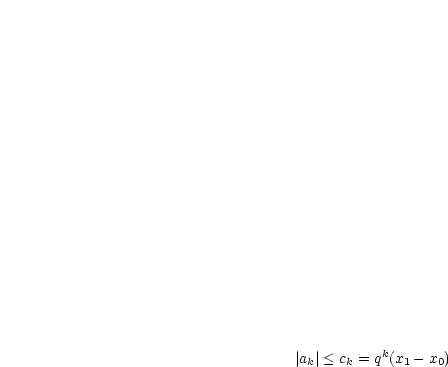
|ak|< ck = qk(x1 - x0)

Wir haben somit eine konvergente Majorante. $oo sum (xk+1 - xk) k=0$ konvergiert, da $sum oo k q k=0$ konvergiert. Somit ist auch die Folge $(xn)$ eine Nullfolge und $xn$ $'--> q$ für $n '--> oo$ und $q (- [a,b]$ .
$f$ ist außerdem stetig, daher können hier die Grenzübergänge vertauscht werden:

( ) lnim'--> oo xn+1 = f(xn) ==> q = lnim'--> oo f(xn) = f nli'-->m oo xn = f(q)

$q$ ist der einzige Fixpunkt. Aus $j = f(j)$ folgt $(q - j) = |f(q)- f (j)|< q.(q- j)$ . Daraus resultiert schlußendlich:

/=0 -- -- 0 < (1--q)|q--j|< 0 =0

Und somit gilt:

q = j

Fehlerabschätzung:

|q- xn|= |f (q)- f(xn))+ f(xn)- f(xn-1)|< |f (q)- f(xn)|+|f(xn)- f(xn-1)| < q|q-xn|+q|xn- xn-1|

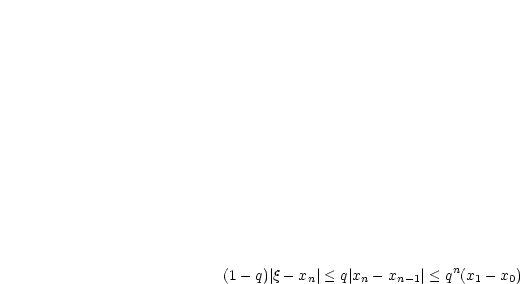
(1- q)| q -xn |< q| xn - xn-1|< qn(x1 - x0)

Beispiel:

g(x) = ex - 3x2 = 0

In $(0,1)$ gibt es eine Nullstelle. Wir bringen die Gleichung auf die Form, so daß ein $x$ auf der linken Seite steht:

x = -1ex = f(x ) 3x 0

Dieses Ergebnis ist jedoch nicht brauchbar, weil die Voraussetzungen nicht erfüllt sind. Deshalb logarithmieren wir die Gleichung zuerst:

x 2 e = 3x

x = ln3 + ln(x2)

Damit folgt:

|--------------------| |x = ln 3+ 2lnx = f(x) | ---------------------

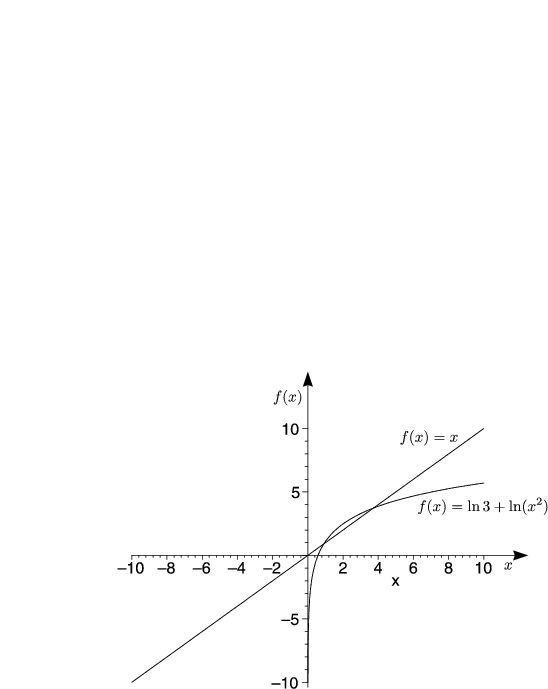
Hier sind nun die Voraussetzungen erfüllt.

$f : (0,1) '--> (0,1)$
$|f(x)|< 1,r (- [a,b] 2$

Als Startwert verwenden wir $x0 = 4$ , woraus dann folgt:

x1 = ln 3+ 2lnx0 = ln3 + 2ln4 = 3,8712

x = ln3 + 2ln x = ln3 +2 ln 3,8712 = 3,8057 2 1

x3 = 3,7716

x4 = 3,7536

x5 = 3,7441

x6 = 3,7390

|x-=-3,7362| --7---------

Hier brechen wir ab und setzen zur Probe in die ursprüngliche Gleichung ein:

x 2 g(x) = e - 3x = 0

3,7362 2 e - 3(3,7362) = 0,061

Die Übereinstimmung ist also recht gut; wir erhalten einen Fehler von $0,15%$ .

8.7.2 NEWTON-Verfahren

P(x)g(x)+x = x --- --- =f(x)

f'(x) = P'(x)g(x)+ P(x)g'(x)+ 1 ~~ 0

P(x) = --1-- g(x)

==> x - g('x)-= x ---g(x) f(x)

xn+1 = xn- g('xn)- g(xn)

$' |f (x) < q < 1|$ läßt sich formulieren als Bedingung aus $' '' g,g ,g ,...$ . Wenn $'' f (x) > 0$ (Funktion ist konvex), dann konvergiert die Folge.

Nebenbemerkung zu Übungsblatt XII (Aufgabe 7):

k g(x) = x - a = 0(a > 0),k (- N

xk- a xn+1 = xn - -nk-1g(x) = xk - a kxn

xk0 > a

[prev] [prev-tail] [front] [up]