|
Es sei |
|
|
Es sei |
|
![f (- C[a,b] ==> f besitzt in [a,b] ein Maximum und ein Minimum. f (p) = max{f(x)| x (- [a,b]},p (- [a,b].](ma3668x.gif)
![p = a ==> f (a) = f(b) > f(x) A (- [a,b]](ma3669x.gif)





 :
:  sei beliebig.
sei beliebig.
 für gewisse
für gewisse  .
.  Minimum
Minimum
![{f(x),x (- [a,b]}= f(q)](ma3680x.gif) mit
mit  .
.  :
: 

|
|
|
|
|
Wende den Satz von ROLLE auf  an.
an.

|
Es sei |
|
|
|


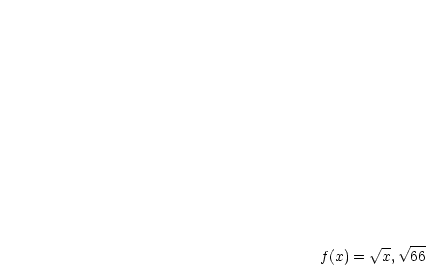
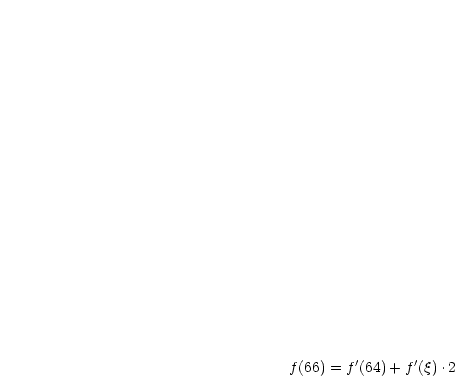

Mit dem Mittelwertsatz können beispielsweise Grenzwerte bestimmt werden:

Wir bringen den Term auf eine Form, auf die man den Mittelwertsatz anwenden kann:
![V~ ---------- V~ --------- [ V~ --------- ]
3 V~ ------- V~ 3- 3 ( a2) 3 V~ -- 3 V~ --3 (a )2 3 V~ -- V~ 3- 3 (a)2
(an) = n2 + a2- n2 = n2 1 + n2 - n2 = n2 1+ n- - n2 = n2 1 + n- - 1 =
[ V~ ------- ]
3 V~ ---(a)2---- 3 V~ ----(a)2--- 3 V~ -- 31 + (a)2- 1 .3 V~ a2-
= --1+ V~ -n---1-= --1-+ V~ -n---1 . V~ -a2=------- V~ n---------- =
3-1 3 1- 3 a2 3(a)2
( n V~ 2------- n2) n
V~ - 31 + (a)2- V~ 31-+-02
= 3a2 ---- V~ (-n)-- V~ -----
3 an - 302](ma3705x.gif) | (8.4) |
Wir vergleichen mit dem Mittelwertsatz:

Dann folgt:


Wir leiten die beiden Funktionen ab:


Daraus ergibt sich dann:
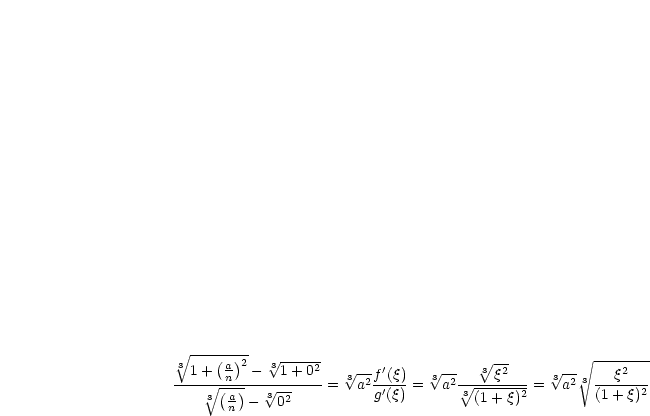
Für  gilt nun
gilt nun  und somit
und somit  . Dann resultiert:
. Dann resultiert:
![|_ V~ ------- _|
( V~ ------- V~ -) 3 1+ (a)2- V~ 31-+-02 [ V~ - V~ ---2---] |-|
lim 3n2 + a2 - 3n2 = lim |_ ---- V~ (n-)- V~ ----- _| = lim 3a2 .3 --q--2- = -0-
n'-->o o n'--> oo 3 an - 3 02 q'-->0 (1+ q)](ma3715x.gif)
• Beispiel 2:

Durch Umformung folgt wieder:

Nach dem ersten Mittelwertsatz gilt:

Dann folgt daraus:

Hierbei gilt nun, wie man unschwer sieht:


Daraus folgt dann schließlich:

Für  gilt nun
gilt nun  und somit
und somit  :
:
![( ) [ 1] ---
lim n 1- cos-1 = lim - cos0--cosn- = lim sin(q) = 0 |
n'--> oo n n'--> oo 0- 1n q'-->0 ---](ma3726x.gif)
|
|
|
|
|
|
|
Daraus ergibt sich |
|
|
|
|


|
Es sei |
|
Betrachte:

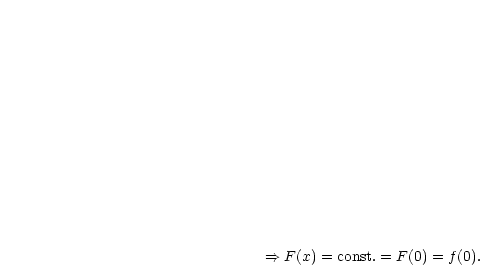
 ist die gesuchte Lösung des folgenden Problems:
ist die gesuchte Lösung des folgenden Problems:  , mit
, mit
 und
und  .
.

Betrachte  ,
, 
 und setze
und setze
 .
.


Wir entkoppeln:

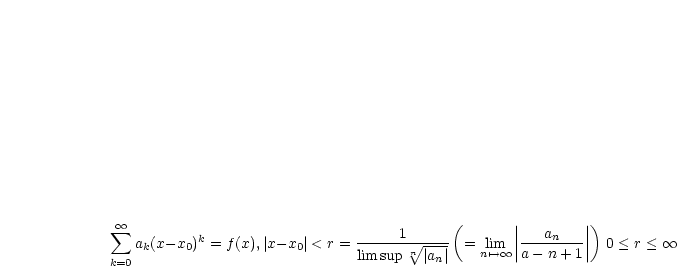
 ist stetig für
ist stetig für  . Die Reihe konvergiert absolut für
. Die Reihe konvergiert absolut für  und
gleichmäßig für
und
gleichmäßig für 
 . Die Reihe ist für
. Die Reihe ist für 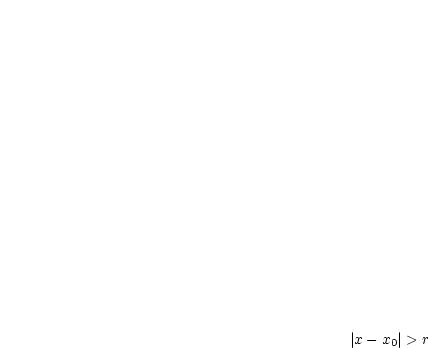 divergent.
divergent.


Betrachten wir den TAYLORsatz für  ,
, ![x0 (- [a,b]](ma3813x.gif) ,
, ![f (- Cn[a,b]](ma3814x.gif) . Es gibt ein
. Es gibt ein
 , so daß gilt:
, so daß gilt:

![n [1 (n) ]
(~T) = Tn- 1(x)+ (x - x0) n!f (x0)+ o(1) (x '--> x0)](ma3817x.gif)

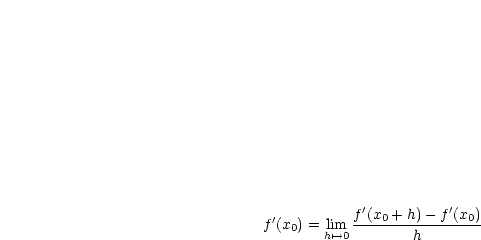




|
|
Ist |
|
Ist |
|
|
|
|
|
|
|
|
|
 : Wende
: Wende  auf
auf  an; ersetze
an; ersetze  durch
durch  .
.
![[ ]
'' n- sum 31- ''(k) k n-2 ---1--- (n)
f (x) = k!(f ) (x0)(x- x0) +(x - x0) (n- 2)!f (x0)+ o(1)
k=0-------- ---------- --------- ---------
=0 hat festen Vorzeichenwechsel](ma3855x.gif)
|
Es sei |
|
|
|
|
|
 . Diskutiert wird die hierdurch
gegebene Funktion.
. Diskutiert wird die hierdurch
gegebene Funktion.
 . Gesucht ist die Potenzreihe, die diese Funktion darstellt.
. Gesucht ist die Potenzreihe, die diese Funktion darstellt.
|
Gegeben sei die Potenzreihe
|

Spezialfall: Wir nehmen an, daß  :
:

Man folgere, daß  für
für  . Außerdem ist zu verwenden:
. Außerdem ist zu verwenden:

Des weiteren nütze man folgende Abschätzung:
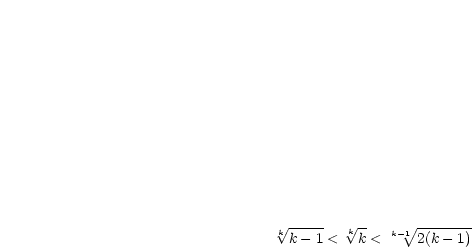
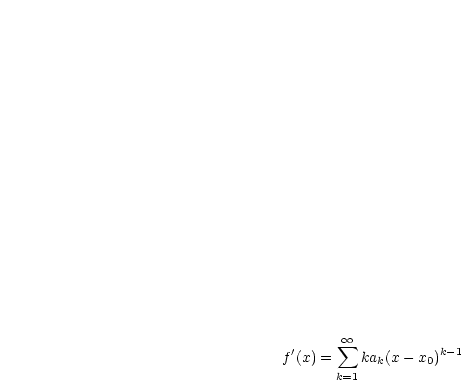
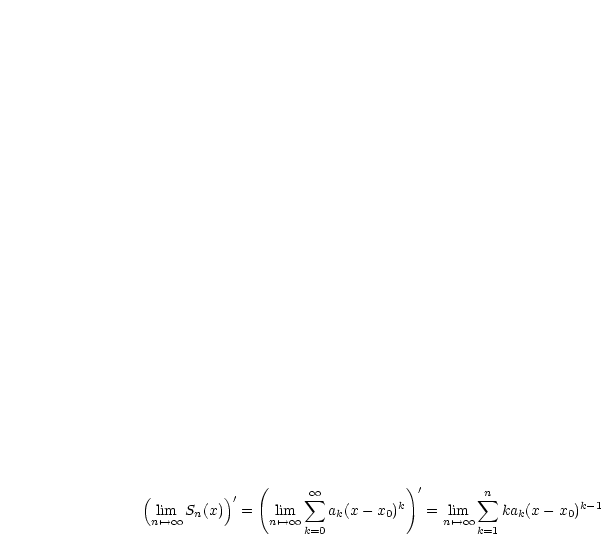

Es handelt sich also um die Vertauschung von zwei Grenzübergängen. Die notwendige Begründung wird später bei der Integralrechnung geliefert.

Aus dieser Reihendarstellung der Funktion  lassen sich die Koeffizienten
ablesen:
lassen sich die Koeffizienten
ablesen:

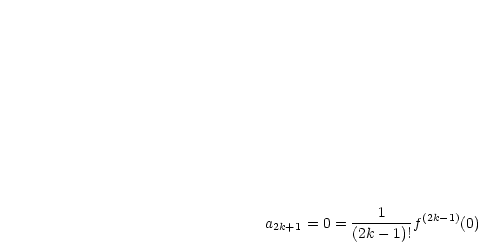
Der Grenzwert kann mittels der Geometrischen Reihe berechnet werden:
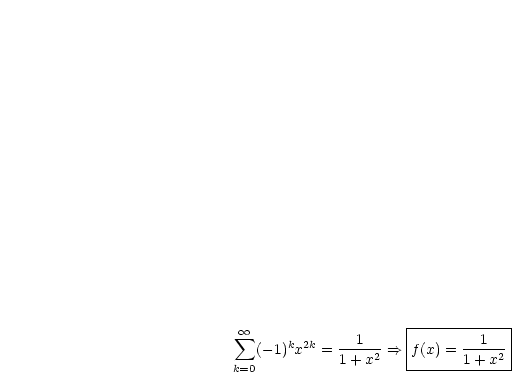

Es gilt  und außerdem dem Zusammenhang
und außerdem dem Zusammenhang  mit
mit
 . Zur Erinnerung:
. Zur Erinnerung:






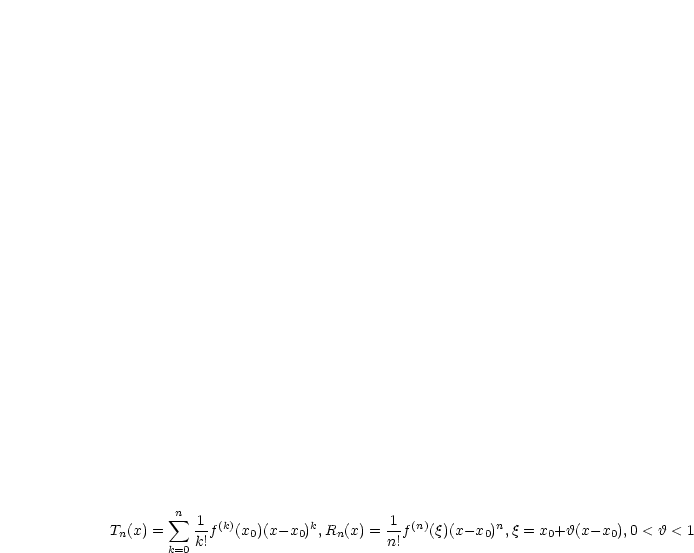
Der Taylorsatz lautet:










Wir multiplizieren mit  :
:
![( ) ( ) ( ) ( )
' sum oo a k sum oo a k+1 oo sum a k oo sum a k
(1+ x)f(x) = (k+ 1) k + 1 x + (k+ 1) k + 1 x = (k + 1) k+ 1 x + k k x =
k= oo 0 ( ) k= oo 0 ( ) oo [ k(=0 ) ( )] k=1
= sum (k+ 1) a xk + sum k a xk = sum (k +1) a + k a xk = af(x)
k=0 k + 1 k=0 k k=0 --------k+ 1------k--
a(a)
k](ma3913x.gif) | (8.5) |
Somit gilt:

Wir multiplizieren diese Gleichung mit  durch, woraus dann
folgt:
durch, woraus dann
folgt:

Der Ausdruck auf der linken Seite stellt gerade die Ableitung folgender Funktion dar:

Somit folgt:

Damit folgt dann durch Aufleiten:

Mit  ergibt sich nun durch Einsetzen von 0 für die Konstante:
ergibt sich nun durch Einsetzen von 0 für die Konstante:

Somit gilt also:
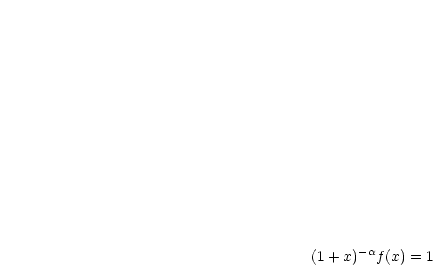
Daraus ergibt sich dann endgültig die binomische Reihe:
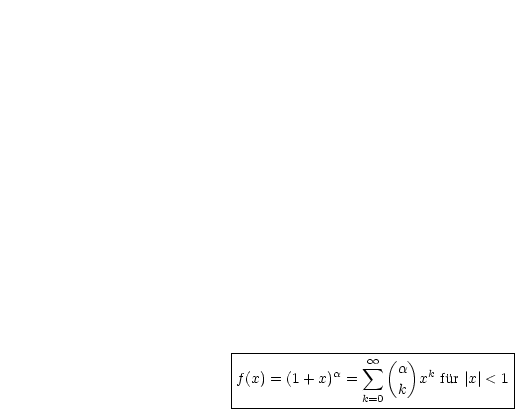
Mittels der binomischen Reihe kann man also Funktionen der Form  entwickeln.
entwickeln.
 folgt beispielsweise:
folgt beispielsweise:

Damit folgt nun:

Wir führen außerdem die Variablentransformation  durch:
durch:

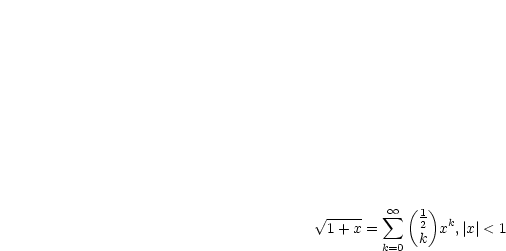
 können wir die Wurzelfunktion entwickeln:
können wir die Wurzelfunktion entwickeln:


Hiermit kann man nun näherungsweise den Wert von  bestimmen:
bestimmen:

Gegeben sei  auf
auf  mit
mit  . Für welche
. Für welche  kann
kann  in eine
Potenzreihe um
in eine
Potenzreihe um  entwickelt werden? Gesucht sind
entwickelt werden? Gesucht sind  und
und  , so daß
, so daß
 gilt.
gilt.
|
|
Es sei |
|


Wir vermuten den folgenden Zusammenhang:

Als Übung kann man den Beweis durch vollständige Induktion erbringen.
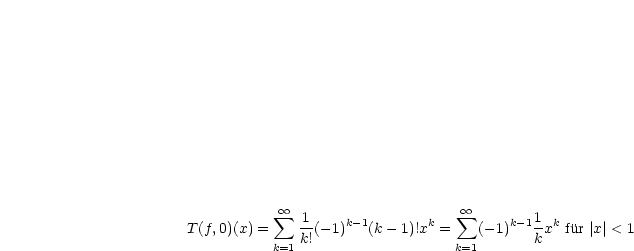
 konvergiert die Reihe von
konvergiert die Reihe von  ?
?
![x (- (-1,+1]](ma3962x.gif) , für die
, für die 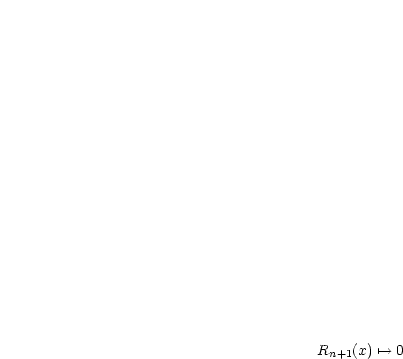 für
für  .
.



Das Ergebnis ist:

Wir zeigen hier zunächst:

 schätzen wir folgendermaßen ab:
schätzen wir folgendermaßen ab:

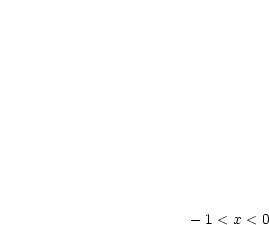 schätzen wir mittels der Dreiecksungleichung ab:
schätzen wir mittels der Dreiecksungleichung ab:

Somit folgt dann:

 ist monoton wachsend.
ist monoton wachsend.

Wir notieren uns nun die Reihe:

 soll um
soll um  entwickelt werden mit
entwickelt werden mit  . Damit
folgt:
. Damit
folgt:
