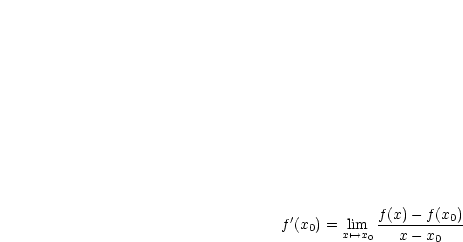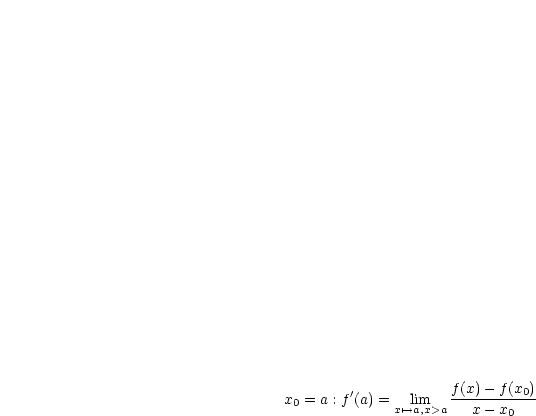|
|
|
|
|
|
|
|
|
 sei lokales Maximum.
sei lokales Maximum.

Für ![f[a,b] '--> R](ma3599x.gif) sollen Extremwerte berechnet werden. Kandidaten dafür
sind:
sollen Extremwerte berechnet werden. Kandidaten dafür
sind:

 nicht differenzierbar ist.
nicht differenzierbar ist.
 mit
mit 
Aus  folgt nicht, daß bei
folgt nicht, daß bei  ein Extremwert vorliegt.
ein Extremwert vorliegt.

|
|
|
![f(x) = x3- x,[-1,2]](ma3613x.gif)
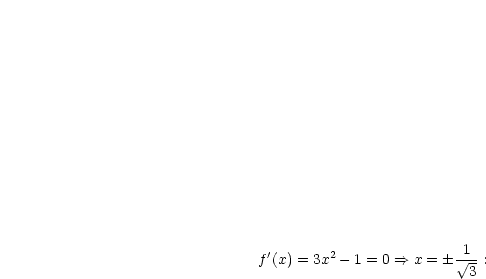
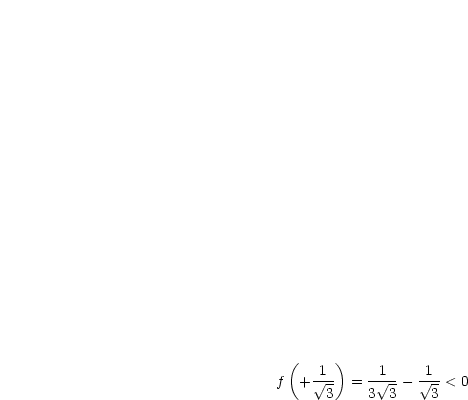
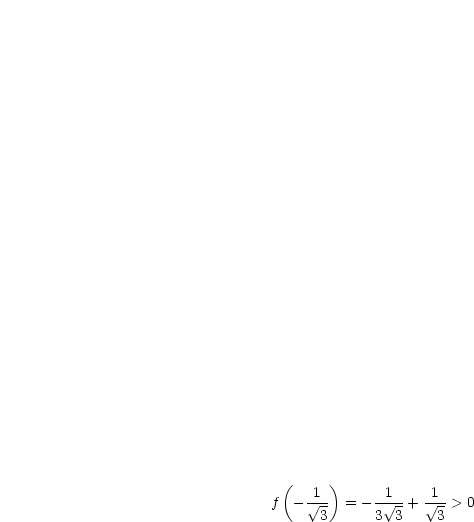

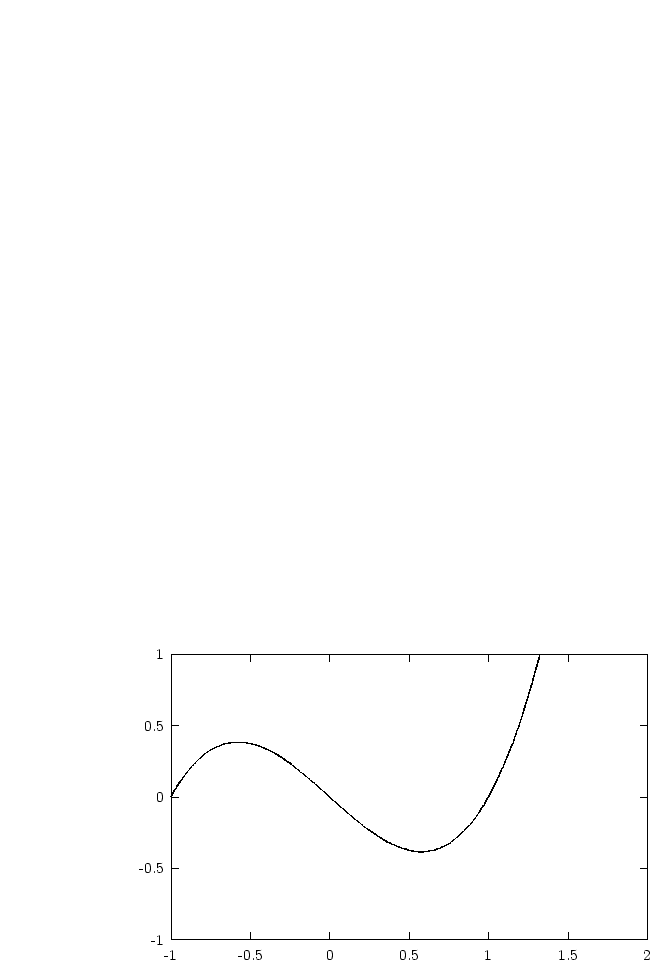
Wir notieren uns folgendes Polynom:
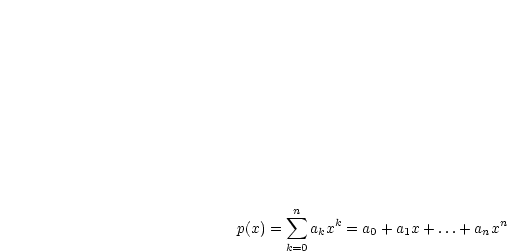
Diese Polynom leiten wir nun  mal ab, woraus sich dann ergibt:
mal ab, woraus sich dann ergibt:
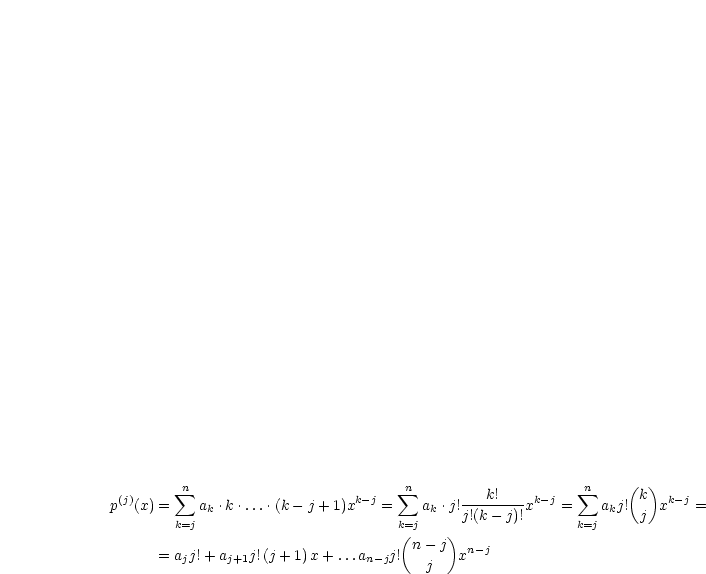 | (8.3) |
Daraus folgt dann für  :
:


 ist stetig in
ist stetig in  .
. 
 ist differenzierbar in
ist differenzierbar in  (
( ,
,
 ).
).
 ist stetig in
ist stetig in  .
. 
 ist differenzierbar in
ist differenzierbar in  (
( ,
,
 ).
).
 sei differenzierbar auf
sei differenzierbar auf  .
. 
 ist auf
ist auf  definiert.
definiert. 
 ist
stetig.
ist
stetig.
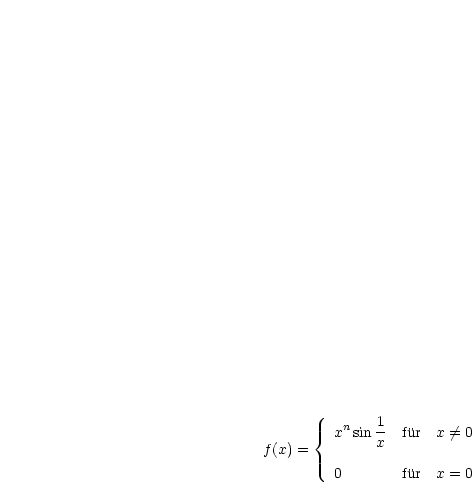
Es sei  :
:  existiert für jedes
existiert für jedes  , aber
, aber  ist in 0 unstetig.
ist in 0 unstetig.