9.1 Berechnung des Flcheninhalts unter einer Kurve

9.1 Berechnung des Flächeninhalts unter einer Kurve

Gesucht ist der Flächeninhalt
Gesucht ist eine Funktion, deren Ableitung wieder die Funktion selbst ist.

Wir wollen uns zuerst mit dem zweiten Problem beschäftigen. Wir zerlegen die Funktion in Streifen:

a = x < x < x < ...< x < x = b 0 1 2 n- 1 n

Es sei $Zn$ : $(x0,x1,...,xn)$ die Zerlegung von $[a,b]$ in $n$ Intervalle $Ik = [xk-1,xk]$ für $k = 1$ , 2, $...$ , $n$ , wobei $Dk = xk - xk- 1$ und $l(Zn) = max{Dk$ für $k = 1$ , 2, 3, $...$ , $n}$ . Wähle nun

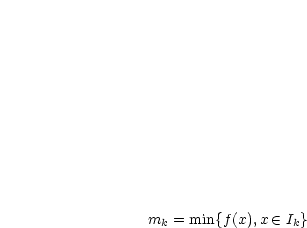
$mk = min{f(x),x (- Ik}$
$Mk = max{f (x),x (- Ik}$

und bilde:

n n w(Z ) = sum m D und _O_(Z ) = sum M D n k=1 k k n k=1 k k

Darüber hinaus wähle $qk (- Ik$ und bilde $sum n f(qk).Dk = S(Zn) k=1$

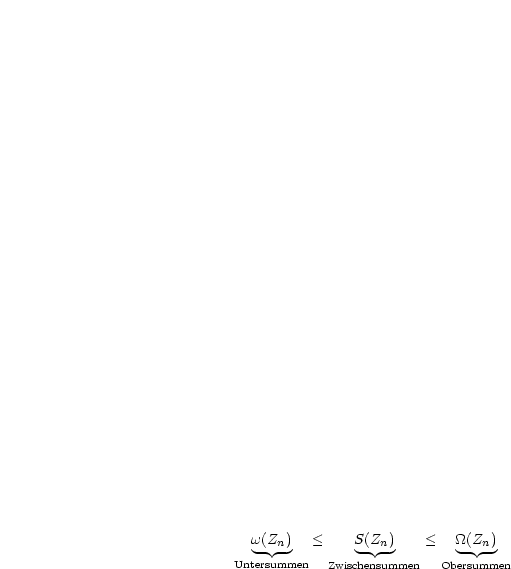
w(Zn) < S(Zn) < _O_(Zn) Untersummen Zwischensummen Obersummen

$w(Z)$ ist monoton wachsend (Zerlegung von $[a,b]$ ), mit $l(z) '--> 0$
$_O_(Z)$ ist monoton fallend (Zerlegung von $[a,b]$ ), mit $l(z) '--> 0$
$I(f) = sup(w(Z))$ , $Z$ ist Zerlegung von $[a,b]$ , $l(Z) '--> 0$
$- I(f) = inf(_O_(Z))$ , $Z$ ist Zerlegung von $[a,b]$ , $l(Z) '--> 0$

Definition:

Falls $- I(f) = I(f)$ gilt, so heißt dieser gemeinsame Wert das bestimmte Integral von $f$ über $[a,b]$ . Wir schreiben dafür:

$b integral sum n f (x)dx = nli'-->m oo f(qk)Dk a ---k=1 ------ f¨ur jede Zerlegung Zn mit l(Zn)'-->0 (n'-->o o )$

Eine Möglichkeit, $Zn$ zu wählen, ist die äquidistante Zerlegung:

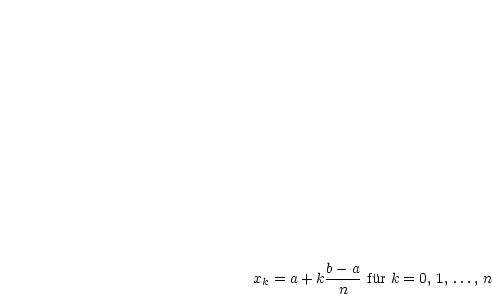
x = a + kb--a-fur k = 0, 1, ..., n k n ¨

b- a Dk = --n--

Damit sehen die Ober- und Untersummen folgendermaßen aus: Mit $qk = xk$ haben wir:

integral b b- a n sum ( b- a) f(x) dx = nl'-->imo o -n-- f a + k--n-- a k=1

Satz:

Es sei $f$ stetig auf dem beschränkten Intervall $[a,b]$ . Dann existiert $integral b f(x)dx a$ . Man kann $integral b f (x)dx a$ beispielsweise durch $( ) b--a- sum n b--a- nl'-->imo o n f a+ k n k=1$ berechnen.

Beispiele:

Beispiel 1: $|--------------| | n sum -1 n | nli'-->mo o n2 +-k2| -----k=0---------$
Daraus folgt:
$n-1 n-1 n-1 S = sum --n----= sum 1----1----= sum (x - x )f(x ) n k=0 n2 + k2 k=0n 1+ (kn)2 k=0 k+1 k k$

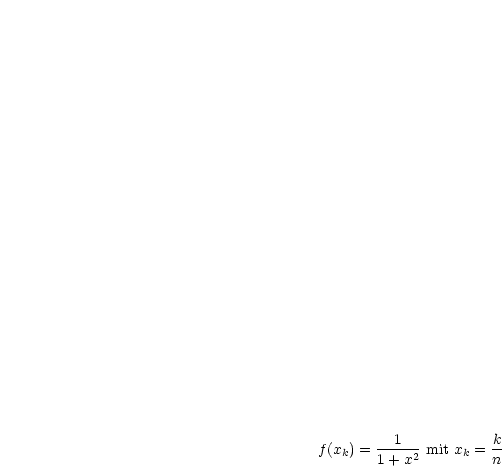
$1 k f(xk) = 1-+-x2 mit xk = n$
$xk$ liefert für $k = 0$ , $...$ , $n- 1$ eine äquidistante Einteilung des Intervalls $[0;1]$ . Dann ergibt sich für den Grenzwert:
$n- 1 integral 1 lim S = lim sum 1----1---= --1---dx = [arctan]1= p n'-->o o n n'-->o o k=0 n1 + (k)2 1+ x2 0 4 n 0$
Beispiel 2: $-------------- | n sum | |lim --1--| n'-->o o -k=1-n+-k-$
Dann ergibt sich durch Umformung:
$sum n sum n sum n Sn = --1--= 1--1-k = (xk - xk- 1)f(xk) k=1n +k k=1 n1 + n k=1$

$-1--- k- f(xk) = 1+ x mit xk = n$
$xk$ liefert für $k = 1$ , $...$ , $n$ eine äquidistante Einteilung des Intervalls $[0;1]$ . Dann ergibt sich für den Grenzwert:
$sum n 1 1 integral 1 1 |---| lim Sn = lim -----k-= -----dx = [ln(1+ x)]10 =-ln-2 n'-->o o n'-->o o k=1n 1+ n 0 1+ x$
Beispiel 3: $|-----n--------| | sum ---k---| nl'-->imo o n2 + k2| -----k=1---------$
Dann ergibt sich:
$sum n k n sum 1 k Sn = n2 +-k2-= n-.---n(k)2-= nli'-->m oo (xk - xk-1)f(xk) k=1 k=1 1+ n$

$--x--- k- f(xk) = 1 + x2 mit xk = n$
$x k$ liefert für $k = 1$ , $...$ , $n$ eine äquidistante Einteilung des Intervalls $[0;1]$ . Dann ergibt sich für den Grenzwert:
$integral 1 [ ] |-----| sum n 1 ---kn---- --x--- 1 2 1 |1 | nl'-->imo o Sn = nl'-->imo o n .1+ (k )2 = 1+ x2 dx = 2 ln(1+ x ) 0 =-2-ln-2| k=1 n 0$
Beispiel 4:
Folgender Grenzwert soll ermittelt werden:
$|--------------| | 1-n sum n V~ --k| nl'-->imo o n e | -------k=1-------$
Wir formen $Sn$ um:
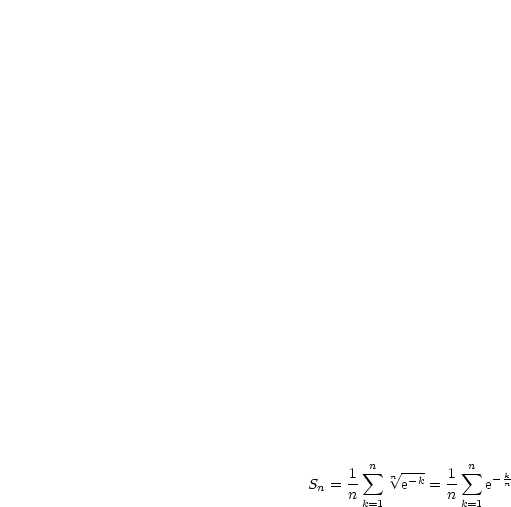
$1 sum n n V~ --k 1- sum n -k Sn = n e = n e n k=1 k=1$
Dann folgt:
$n n 1- sum -kn sum Sn = n e = (xk - xk- 1)f(xk) k=1 k=1$

$k f(xk) = e-x mit xk =- n$
$xk$ liefert für $k = 1$ , $...$ , $n$ eine äquidistante Einteilung des Intervalls $[0;1]$ . Dann ergibt sich für den Grenzwert:
$1 integral -x [ -x]1 1 lnim'--> oo Sn = e dx = -e 0 = 1 - e 0$

Beispiel 5:

Der Grenzwert folgendes Produktes soll ermittelt werden:

|----------------| | 1 n prod -1| nli'-->mo o -- (n +k)n | -----nk=1---------

Wir formen das Produkt in eine Summe um:

( [ ]) ( [ ] ) 1-n prod n1 1- prod n 1n 1- sum n 1n n (n +k) = exp ln n (n + k) = exp ln n + ln(n + k) = k=1 ( [ ]k=1 n ) ( [ k=]1 n [ ( )]) = exp ln 1- + 1- sum ln(n + k) = exp ln 1- + 1- sum ln n 1+ k- = n n k=1 n n k=1 n ( n ( )) ( n ( )) = exp - ln n+ 1-.n lnn + 1- sum ln 1 + k- = exp -1 sum ln 1+ k- = n n k=1 n n k=1 n ( sum n ) = exp (xk- xk-1)f(xk) k=1

(9.1)

Damit gilt:

k f(xk) = ln(1 + x) mit xk = n

$xk$ liefert für $k = 1$ , $...$ , $n$ eine äquidistante Einteilung des Intervalls $[0;1]$ . Dann ergibt sich für den Grenzwert:

( ) ( 1 sum n ( k)) integral 1 ( ) nli'-->m oo exp -- ln 1 + -- = exp ln(1+ x)dx = exp [(1 + x)ln(1 +x) - (1 + x)]10 = n k=1 n 0 4-| = exp(2ln2 - 1) = exp(- 1).exp(2ln 2) = exp(-1).exp(ln 4) = 4exp(-1) = | -e-

(9.2)

• Beispiel 6:

Es soll der Grenzwert folgender Summe berechnet werden:

|-----------------| | sum oo 1 sum 2n kj| |nli'-->m oo -- -j+1| -----j=0-j!k=1-n----

Diese Summe formen wir um:

oo sum 2 sum n j oo sum sum 2n j oo sum 2 sum n ( )j oo sum 2 sum n 1- -kj+1 = 1- -jk-- = 1- 1- -k = 1- (xk- xk-1)f(xk) j=0 j!k=1n j=0j!k=1n .n j=0 j!k=1n n j=0 j!k=1

Nun gilt:

f(x) = xj mit xk = k n

$xk$ liefert für $k = 1$ , $...$ , $2n$ eine äquidistante Einteilung des Intervalls $[0;2]$ . Daraus folgt nun für den Grenzwert:

2 oo sum 1- sum 2n-1(k-)j oo sum 1- integral j sum oo 1--1--[ j+1]2 oo sum 1---1-- j+1 oo sum --1----j+1 ln'-->imo o j! n n = j!. x dx = j!.j + 1 x 0 = j!.j + 1.2 = (j + 1)!2 j=0 k=1 j=0 0 j=0 j=0 j=0

Dies ist nun nichts anderes als die Reihenentwicklung für die Exponentialfunktion. Damit ergibt sich nun:

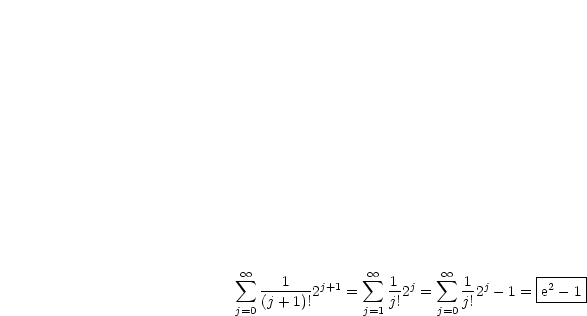
sum oo sum oo oo sum |-----| --1---2j+1 = 12j = 1-2j - 1 =-e2--1- j=0 (j + 1)! j=1 j! j=0 j!

Folgende Definitionen sind unmittelbar klar.

Definitionen:

$integral a integral b integral a f(x)dx = 0, f(x)dx = - f(x) dx a a b$
$c$ , $r (- C$ ; $f$ , $0 g (- C [a,b]$ . Dann gilt: $b b b integral integral integral (cf(x)+ rg(x)) dx = c f(x)dx +r g(x)dx a a a$
Für komplexe Funktionen gilt: $f(x) = u(x)+ iv(x)$ : $integral b integral b integral b f(x)dx = u(x)dx+ i v(x)dx a a a$
$a < b < g$ : $integral b integral g integral g f(x)dx + f(x)dx = f(x)dx a b a$
Es sei $f$ auf $[a,b]$ stückweise stetig, d.h. es gibt endlich viele Unstetigkeiten $a1$ , $...$ , $an$ ( $a1 < a2 < ...< an$ ), wobei $lxi'-->ma f(x) j$ und $x'-->liam+ f(x) j$ existieren. Dann wird definiert:
$integral b a integral 1 n sum -1a integral j+1 integral b f(x)dx = f(x)dx + f(x)dx + f(x)dx a a k aj an$

Beweis von 4.):

Dies gilt für jede Anordnung von $a$ , $b$ , $g$ zueinander. Es sei $g < a < b$ :

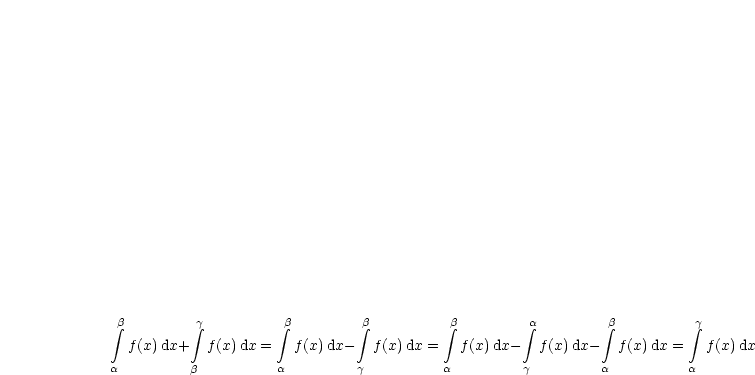
integral b integral g b integral integral b integral b integral a integral b integral g f(x)dx+ f(x)dx = f(x)dx- f(x)dx = f(x) dx- f (x) dx- f (x)dx = f(x)dx a b a g a g a a

Beispiel:

Wir berechnen das Integral von $a$ bis $b$ von $f (x) = x$ :

integral b b- a sum n ( b- a) ( (b - a)2 sum n ) n(n+1) f(x)dx = lnim'--> oo ----- a + k----- = nl'-->imo o a(b- a)+ ----- k 2 = a n k=1 n n k=1 21 1 2 2 = a(b - a)+ (b - a)2 = 2 (b - a )

(9.3)

Beispiel:

integral b n ( ) cosx dx = lim b- sum coskb- n'-->o o n k=1 n 0

Wir benutzen folgende Formel (11.Übungsblatt):

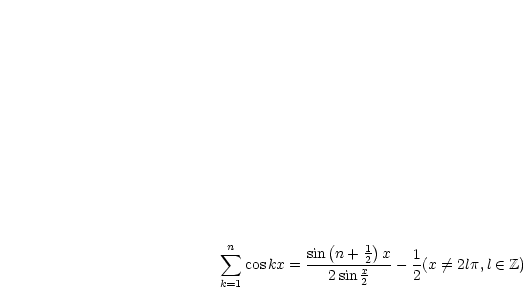
( ) n sum sin-n+--12-x 1 coskx = 2sin x - 2(x /= 2lp,l (- Z) k=1 2

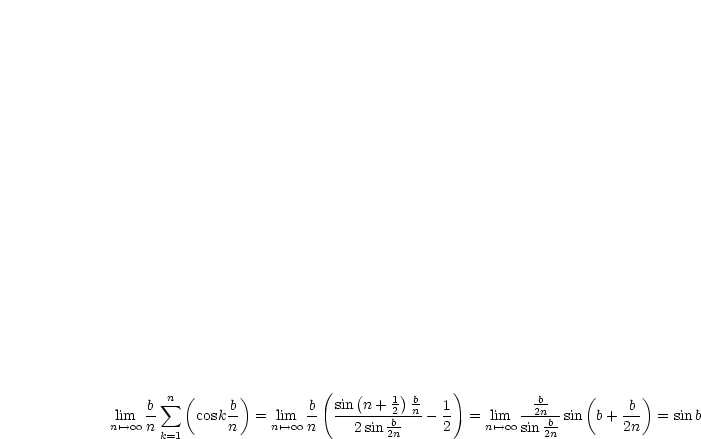
b sum n ( b) b( sin (n + 1)b- 1 ) b- ( b) lni'-->m oo -- cosk -- = nli'-->m oo -- -------2b--n- - = lnim'--> oo --2nb sin b+ --- = sinb n k=1 n n 2 sin2n 2 sin2n 2n

Als nächstes verwenden wir:

integral b integral a integral b cosxdx = cosxdx+ cosxdx = sin b- sin a a 0 0

Definition:

Aus $f(x) > 0$ und $a < y < b$ folgt $integral b f (x)dx > 0 a$ .

Bemerkungen:

$a$ , $b$ bezeichnen wir als Integrationsgrenzen, $x$ ist die Integrationsvariable und $f(x)$ der Integrand.

$b b b integral integral integral f (x)dx = f(t)dt = f(t)dt a a a$

9.1.1 Integration von Ungleichungen

Satz:

Es sei $f$ , $g (- C0[a,b]$ , $f(x) < g(x)$ , $a < x < b$ . Dann gilt $integral b integral b f (x)dx < g(x)dx a a$ .

Beweis:

Wir schreiben $g(x) -f (x) > 0$ . Daraus folgt durch Anwendung der vierten Regel:

integral b (g(x)- f(x))dx > 0 a

Danach wenden wir die zweite Regel an:

b b b integral integral integral (g(x) -f (x))dx = g(x)dx- f(x)dx > 0 a a a

Folgerung:

Es ist $|a|< b <==> -b < a < b$ und außerdem sei $f (- C0[a,b]$ . Jede reelle Zahl können wir nach oben bzw. nach unten durch den Betrag abschätzen:

-|f(x)|< f(x) < |f (x)|

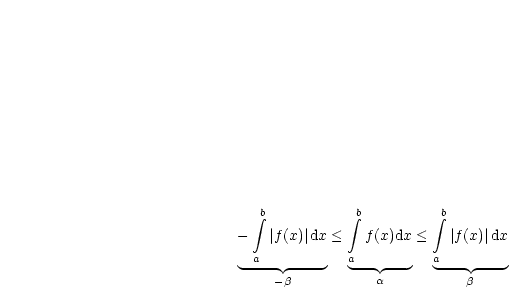
integral b integral b integral b - |f(x)|dx< f(x)dx < |f(x)| dx a a a ---- ---- --- --- ---- ---- -b a b

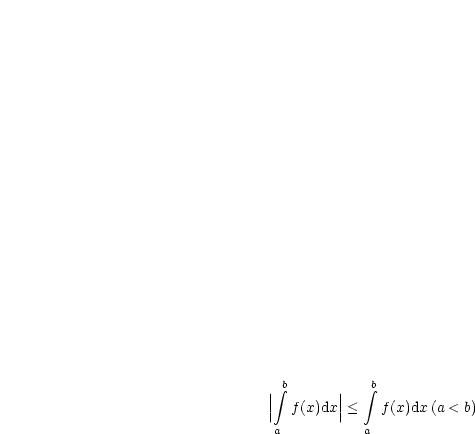
integral b integral b || || | f (x)dx|< f(x)dx (a < b) a a

Dies gilt nach der Dreiecksungleichung! Außerdem können wir daraus folgern:

0 f (- C [a,b] : max{f (x)|a < x < b}= ||f|| > |f(x)|,x (- [a,b]

0 f,g (- C [a,b] :|f(x)g(x)|= |f(x)||g(x)|< ||f|| |g(x)|a < x < b

integral b integral b f(x)g(x)dx < ||f(x)|| g(x)dx a a

integral b g(x) = 1 : |f (x)|dx < ||f||(b - a) a

Satz:

$f1$ , $f2 (- C0[a,b]$ , $f1(x) < f2(x)$ $a < x < b$ . Es sei $G = {(x,y| f1(x) < y < f2(x)$ , $a < x < b}$ . Dann ist der Flächeninhalt von $G$ gegeben durch $integral b I(G) = (f2(x)- f1(x))dx a$ .