9.2 Der Mittelwertsatz der Integralrechnung

[next] [prev] [prev-tail] [tail] [up]

9.2 Der Mittelwertsatz der Integralrechnung

Satz:

$f$ , $g (- C0[a,b]$ , $f(x) > 0$ , $a < x < b$ . Außerdem ändert $f(x)$ im Intervall $[a,b]$ das Vorzeichen nicht. Dann gibt es ein $q (- (a,b)$ $(q = a + h(b- a),a < h < 1)$ mit: $integral b integral b f(x)g(x)dx = g(q) f(x)dx a a$ .

Spezialfall für $f = 1$ :

|--------------------| | integral b | | g(x)dx = g(q)(b - a) -a-------------------|

Beweis:

Wir betrachten eine Funktion $integral b h(t) = g(t) f(x)dx a$ , $a < t < b$ , $h (- C0[a,b]$ .

g(x2) = min{g(x),a < x < b} < g(x) < g(x1) = max {g(x),a < x < b},x1 (- [a,b]

f(x)g(x ) < g(x)f(x) < g(x )f(x),a < x < b. 2 1

integral b h(x2) < g(x)f(x)dx < h(x1) a

Da $h$ stetig ist, gibt es nach dem Zwischenwertsatz ein $q (- (a,b)$ mit $integral b h(q) = f(x)g(x)dx a$ .

Anwendung:

Wir wollen den Grenzwert für $n '--> oo$ folgender Funktionenfolge bestimmen:

|------------------------------| | integral 1 integral 1 | |Fn(x) = fn(x) = --f(x)--dx | | 1 + n2x2 | ---------1---------1-----------

Hier folgt dann mit dem Mittelwertsatz der Integralrechnung:

integral 1 integral 1 --f(x)-- ---1---- F(x) = nl'-->imo o Fn(x) = nli'-->mo o n 1 + n2x2 dx = lnim'--> oo f(q).n 1+ (nx)2 dx = [ - 1 ] -1 1- 1 1- = nl'-->imo o f(q) .n. n arctan(nx) -1 = lnim'--> oo f(q).n. n [arctan(n)- arctan(- n)] = |-----------------------------| = |nli'-->m oo f(q)[arctan(n)- arctan(-n)]| -------------------------------

(9.4)

Für $fn(x)$ folgt für $n '--> oo$ :

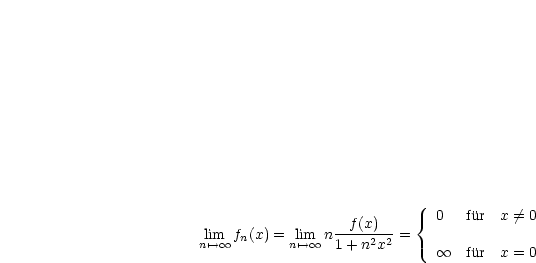
f(x) { 0 f¨ur x /= 0 lim fn(x) = lim n----2-2-= n'--> oo n'-->o o 1+ n x oo f¨ur x = 0

Also nähert sich die Zwischenstelle $q$ für $n '--> oo$ dem Wert 0 an:

|--------------| q-'-->-0-f¨ur-n-'-->- oo -

Dann ergibt sich schließlich:

(p p) |------| F (x) = nli'-->m oo f(q)[arctan(n)- arctan(-n)] = f(0). 2 + 2 = p-.f(0)-

[next] [prev] [prev-tail] [front] [up]