9.10 Uneigentliche Integrale

Vereinbarungen:

Ist $I (_ R$ ein Intervall und $f : I '--> R$ eine Funktion, so gelte $f (- R$ $[q,j]$ für jedes Intervall $[q,j] (_ I$ .
Stets: $a$ , $b (- R$ , $a (- R U {- oo }$ , $b (- R U { oo }$ , $a < b$ , $a < b$ .

Definition:

Es sei $f : [a,b) '--> R$ . Das uneigentliche Integral $b integral f(x)dx a$ heißt konvergent, wenn folglich gilt:

Es existiert der Grenzwert $integral t lim f (x)dx t'-->b-0a$ und ist $(- R$ . In diesem Fall gilt: $integral b f(x)dx a$ : $integral t lim f(x)dx t'-->b-0a$ . Ist $integral b f(x)dx a$ nicht konvergent, so heißt es divergent.

Definition:

Es sei $f : [a,b) '--> R$ . Das uneigentliche Integral $integral b f(x)dx a$ heißt konvergent, wenn folglich gilt: Es existiert der Grenzwert $integral b lim f (x)dx t'-->a+0 t$ und ist $(- R$ . In diesem Fall gilt: $integral b f(x)dx a$ : $integral b tl'-->ima+0 f(x)dx t$ . Ist $integral b f(x)dx a$ nicht konvergent, so heißt es divergent.

Beispiele:

Sei $g > 0$ : $oo t log t f¨ur g = 1 integral 1 integral 1 { xgdx, xg-dx = 1 1-g||t 1 ( 1- g ) 1 1 1---gx || = 1--g- t - 1 f¨ur g /= 1 1$
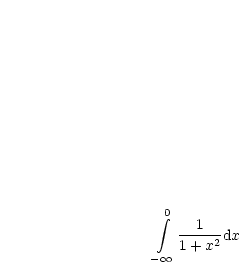
Also konvergiert $oo integral -1- xg dx 1$ für $g > 1$ .
Analog für $g > 0$ : $1 integral 1 xgdx 0$ konvergiert für $g < 1$ .
Beachte: $integral 1 V~ 1-dx x 0$ konvergiert, aber $integral 1( )2 integral 1 1 V~ -- dx = 1-dx x x 0 0$ divergiert.
$integral t 1 p 1-+-x2dx = arctant '--> 2- 0$ für $t '--> oo$ .
Das heißt, daß $oo integral --1---dx 1 +x2 0$ gegen $p 2$ konvergiert.
Analog: $integral 0 --1--2dx - oo 1 + x$ konvergiert gegen $p- 2$ .

Definition:

Es sei $f : (a,b) '--> R$ . Das uneigentliche Integral $integral b f(x)dx a$ heißt konvergent, wenn es ein $c (- (a, b)$ gibt, so daß folgendes gilt:

$integral c f(x)dx a$ und $integral b f(x)dx c$ sind beide konvergent. In diesem Fall gilt:

$integral b integral c b integral f(x)dx := f (x)dx + f(x)dx a a c$ . $integral b f(x)dx a$ heißt divergent, falls es nicht konvergiert.

Übung:

Zeige, daß obrige Definitionen unabhängig von $c (- (a,b)$ sind.

Beispiele:

$oo integral 1 xg-dx 0$ $(g > 0)$ ; $oo integral 1 xgdx 0$ ist divergent.
$oo integral --1--- 1 + x2dx - oo$ ist konvergent und gleich $p$ .

Die folgenden Definitionen und Sätze formulieren wir nur für Funktionen $f : [a,b) '--> R$ . Diese Sätze und Definitionen gelten sinngemäß für die beiden anderen Typen uneigentlicher Integrale.

9.10.1 CAUCHY-Kriterium

Satz:

$b integral f(x)dx a$ konvergiert, wenn $A$ $e > 0$ $E$ $c = c(e) (- (a,b)$ mit $v || integral || | f(x)dx|< e u$ $A$ $u$ , $v (- (c$ , $b)$ .

Beweis:

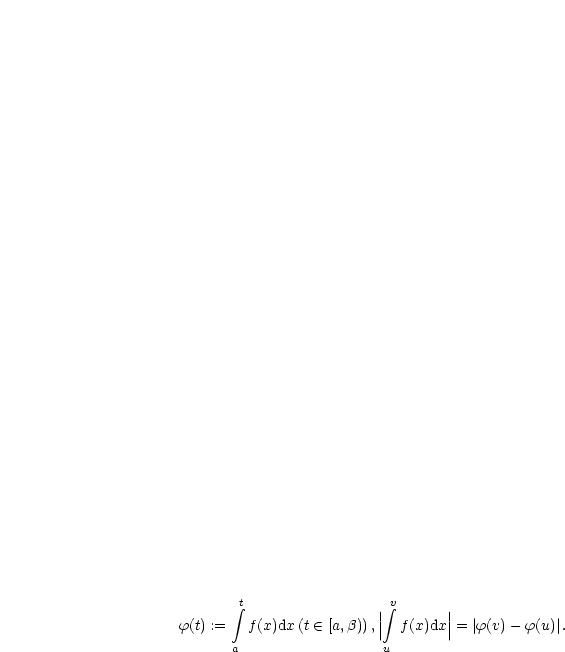
integral t integral v f(t) := f(x)dx(t (- [a,b)),|| f(x)dx||= |f(v)- f(u)| . | | a u

Die Behauptung folgt aus dem CAUCHY-Kriterium bei Grenzwerten von Funktionen.

Beispiel:

Wir behaupten, daß $oo integral sin x -x-- 0$ konvergent ist. Dies wollen wir im folgenden zeigen. Dazu sei $0 < u < v$ :

|| integral v sinx || || integral v 1 || ||[ cosx]v integral v ( 1 ) || | -x-dx |= | x-.sinxdx| = |- -x-- u- - x2 (- cosx)dx|= u u g' u f v v ||cos-u cosv integral cosx || 1- 1 integral 1- 2- = | u - v - x2 dx |< u + v + x2dx = u u u

(9.10)

Damit resultiert dann:

integral v || sinx- || 2- | x dx|< u u

Es sei $e > 0$ : Wähle $u$ , $v$ so, daß $2 u-< e$ und $u < v$ . Dann gilt:

integral v || sin-x || | x dx|< e. u

Daraus folgt die Behauptung.

Definition:

$b integral f(x)dx a$ konvergiert absolut, wenn $b integral |f(x)|dx a$ konvergiert.

\text{[math]}

Ähnlich wie bei Reihen beweist man diese Aussage.

Satz:

Ist $integral b f(x)dx a$ absolut konvergent, so folgt, daß $b integral f(x)dx a$ auch konvergent ist.

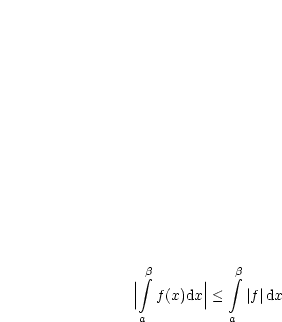$| integral b | integral b || f(x)dx||< |f|dx a a$

9.10.2 Majorantenkriterium

Satz:

Ist $|f| < g$ auf $[a,b)$ und $integral b g(x)dx a$ konvergent, so folgt:

$integral b f(x)dx a$ ist absolut konvergent.

9.10.3 Minorantenkriterium

Satz:

Ist $f > g > 0$ auf $[a,b)$ und $integral b g(x)dx a$ divergent, so folgt:

$b integral f(x)dx a$ ist divergent.

Satz:

In (2) und (3): Sei $g : [a,b) '--> R$ eine Funktion, die integrierbar ist über jedes kompaktes Teilintervall von $[a,b)$ .

Beispiele:

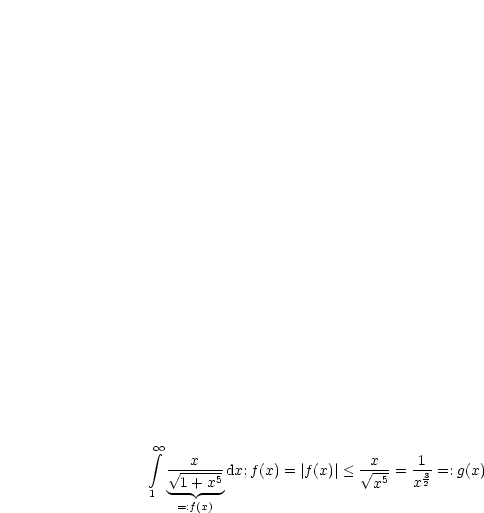$integral oo x x 1 V~ ----5-dx;f(x) = |f(x)|< V~ -5-=-3-=: g(x) 1 -1+ x- x x2 =:f(x)$ , $oo integral g(x)dx 1$ konvergiert.
Also ist auch $integral oo f(x)dx 1$ konvergent.
$integral oo 1 x-dx 1$ divergiert. Daraus ergibt sich:
- $oo integral g(x)dx 1$ ist divergent.
- $integral oo f (x)dx 1$ ist divergent.

[prev] [prev-tail] [front] [up]