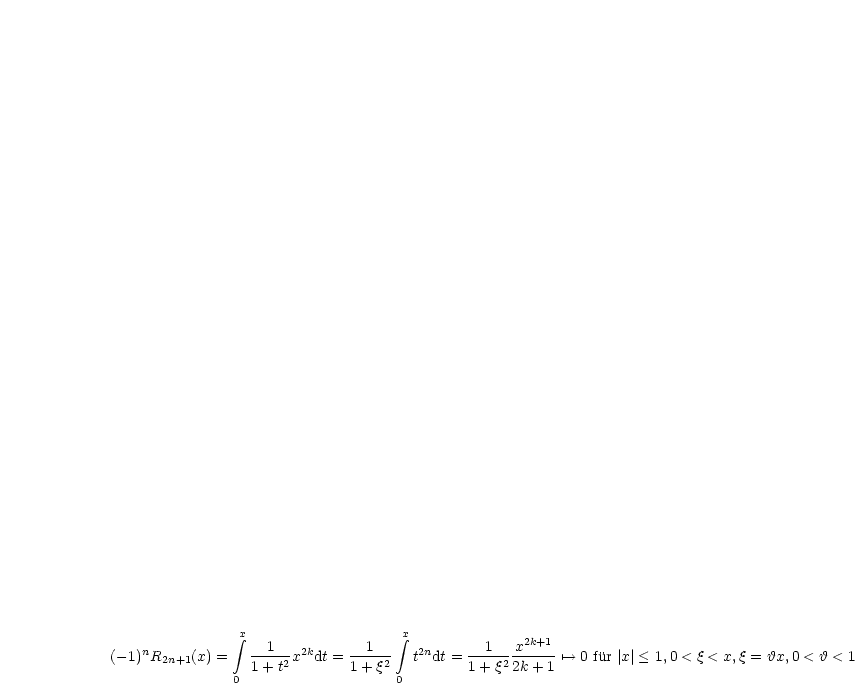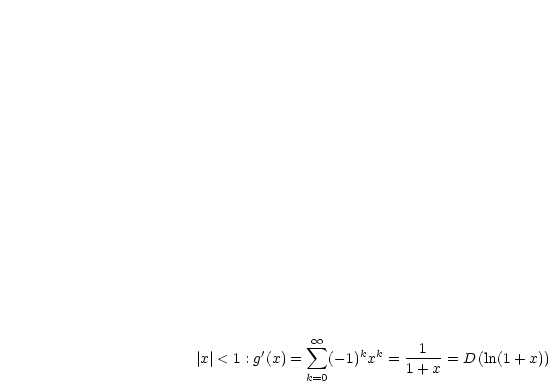9.9 Differentiation und Integration von Potenzreihen

[next] [prev] [prev-tail] [tail] [up]

9.9 Differentiation und Integration von Potenzreihen

Potenzreihen dürfen innerhalb des Konvergenzbereiches gliedweise differenzieren und integriert werden.

Satz:

$integral x sum oo k sum oo integral x k ak(t- x0) dt = ak(t- x0) dt x0k=0 k=0x0$ für $|x- x0|< r$

$(i ntegral k) oo integral k-1 D ak(x - x0) = kak(x - x0) k=0$

Beweis:

Sei $x$ beliebig mit $|x - x0|< r$ . Wähle $r < r$ mit $|x - x0|< r$ .

sum oo k ak(t- x0) = f(t) = nli'-->mo o fn(t) gleichm¨aßig f¨ur|t- x0|< r k=0

g(t) = ln'-->imo o f'n(t) gleichma¨ßig fu¨r |t -x0|< r

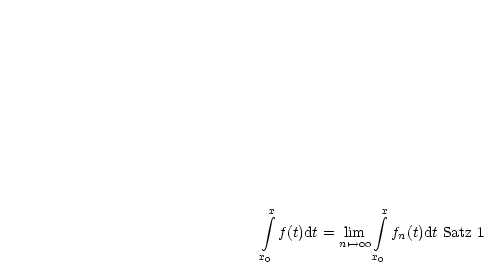
integral x integral x f(t)dt = nl'-->imo o fn(t)dt Satz 1 x0 x0

integral x oo integral x n n integral x oo integral x sum a (t- x )kdt, lim sum a (t- x )kdt = lim sum a (t-x )kdt = sum a (t-x )kdt k 0 n'-->o o k 0 n'-->o o k 0 k 0 x0 k=0 x0 k=0 k=0x0 k=0x0

Nach Satz 2 ist $f'(t) = g(t)$ .

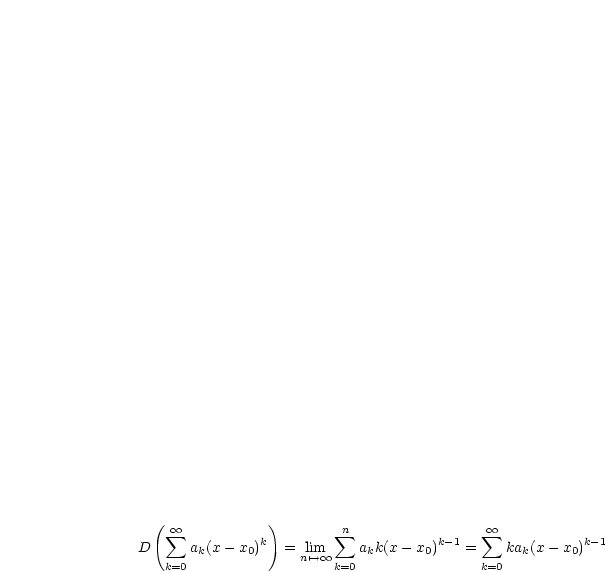
( oo sum ) sum n sum oo D ak(x - x0)k = lim akk(x- x0)k-1 = kak(x -x0)k-1 k=0 n'--> oo k=0 k=0

Beispiel:

Wir suchen die Stammfunktion von $f(x) = e-x2$ :

integral x F(x) = e-t2dt 0

Diese Funktion ist nicht elementar integrierbar. Wir entwickeln den Integranden also zuerst in eine Potenzreihe und integrieren dann:

oo oo e-t2 = sum 1-(- t2)k = sum (-1)k-1t2k k=0k! k=0 k!

integral x 2 oo sum 1 integral x sum oo 1 e- x = (- 1)k k! t2k = (- 1)k(2k-+-1)k!x2k+1 0 k=0 0 k=0

Beispiel:

Wir betrachten den sogenannten Integralsinus:

integral x Si(x) = p-+ sintdt 2 t 0

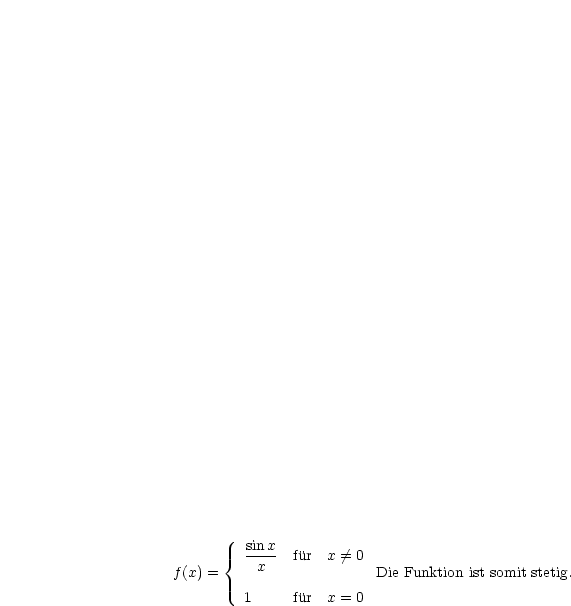
sinx- { x f¨ur x /= 0 f(x) = Die Funktion ist somit stetig. 1 f¨ur x = 0

oo sinx = sum (- 1)k---1---x2k x k=0 (2k + 1)!

Wir integrieren:

integral xsint p sum oo 1 integral x p sum oo 1 1 ----dt = --+ (- 1)k-------- t2kdt = ---+ (-1)k-------------x2k+1 0 t 2 k=0 (2k+ 1)!0 2 k=0 (2k+ 1)!2k+ 1

integral oo sinx-dx = p- 0 x 2

Beispiel:

Wir wollen folgendes Integral berechnen:

|---- integral 1----------| |----------------| | artanh(t)--t| | oo sum (-1)k+1 | |I = t2 |mit dem Hinweis | k = ln2 | -----0------------- -k=1---------------

Die Potenzreihe des Areatangenshyperbolikus lautet:

oo 2n+1 artanh = sum x----- n=0 2n+ 1

Damit ergibt sich nun für das Integral:

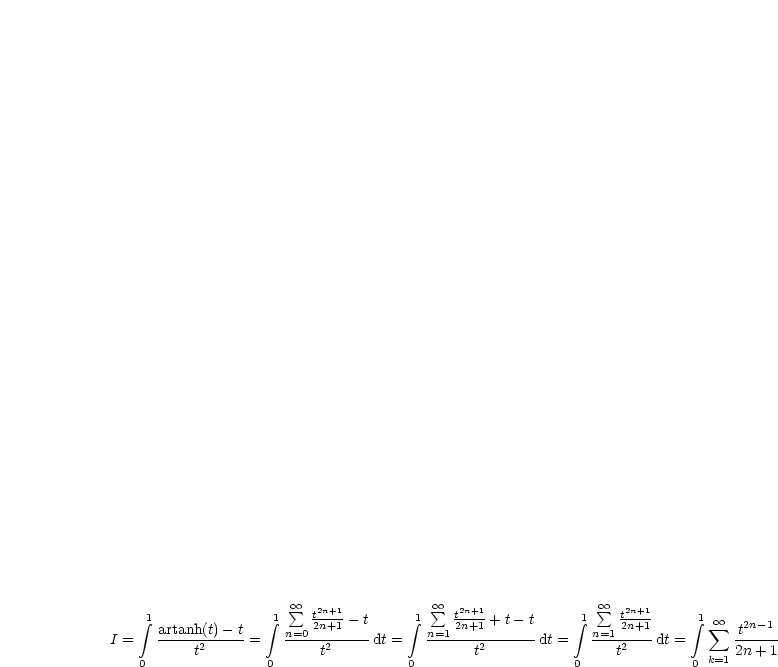
oo sum oo sum oo sum integral 1 integral 1 t22nn++11 -t integral 1 t22nn++11 + t- t integral 1 t22nn++11 integral 1 oo sum 2n-1 I = artanh(t)--t= n=0--------dt = n=1-----------dt = n=1-----dt = t----- 0 t2 0 t2 0 t2 0 t2 0 k=1 2n+ 1

Aufgrund der absoluten Konvergenz können wir Integral und Grenzübergang vertauschen:

oo integral 1 oo [ ]1 oo I = sum t2n-1-dt = sum ----t2n--- = sum ----1---- n=1 2n+ 1 n=1 2n(2n + 1) 0 n=12n(2n + 1) 0

Durch Partialbruchzerlegung folgt nun:

----1---- -1- ---1-- 2n(2n + 1) = 2n - 2n + 1

Somit folgt:

( ) oo sum -1- --1--- oo sum (-1)k sum oo (-1)k I = 2n - 2n + 1 = k = 1+ k n=1 k=2 k=1

Mit dem Hinweis folgt nun:

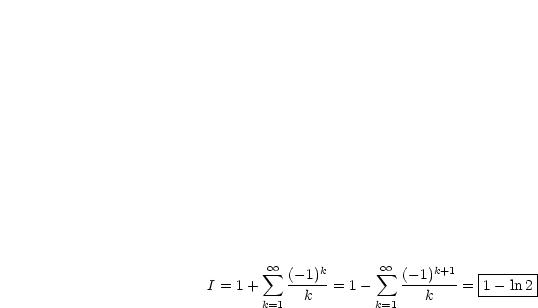
oo sum (-1)k sum oo (- 1)k+1 |------| I = 1+ --k-- = 1- ---k--- = -1--ln-2- k=1 k=1

9.9.1 Entwicklung der Potenzreihe des Arcustangens

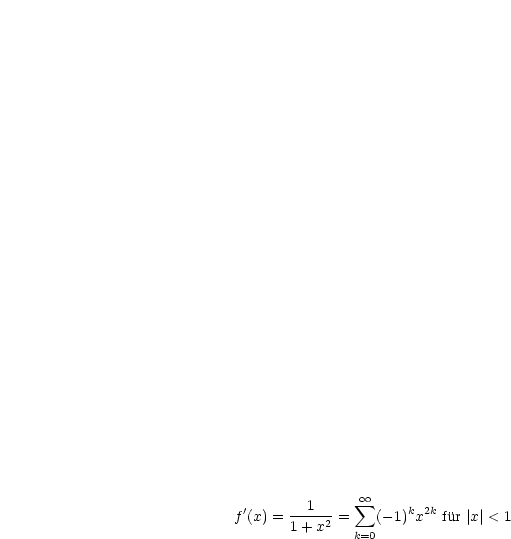
oo f'(x) =--1---= sum (-1)kx2k fur|x|< 1 1 + x2 k=0 ¨

integral x integral oo arctan x = f'(t)dt = (- 1)k --1--x2k+1 f¨ur|x|< 1 0 k=0 2k+ 1

Wir wollen nun die Gleichheit für $x = ± 1$ untersuchen:

n sum -1 1- qn 1 n sum -1 qn qk = 1---q-'--> 1---q = qk + 1--q- k=0 -- -- k=0 q/=1

integral x integral x(n -1 ) integral x 2n n-1 integral x integral x 2n arctan(x) = -dt--= sum (-1)kt2k dt+ (-1)n-t---dt = sum (- 1)k t2kdt+ (- 1)k--t--dt 1+ t2 k=0 1 + t2 k=0 1 + t2 0 0 0 0 0----- ------ R2n+1(x)

integral x 1 (-1)nR2n+1(x) = ----2x2kdt 0 1+ t

Wir erinnern uns an den Mittelwertsatz der Integralrechnung.

f,g (- C0[a,b],f(x) > 0,a < x < b

integral b integral b Dann gibt es ein q (- (a,b) mit f(x),g(x)dx = g(q) f(x)dx a a

integral x integral x 2k+1 (-1)nR2n+1(x) = --1-2 x2kdt = --1-2- t2ndt = --1-2 x----'--> 0 f¨ur|x|< 1,0 < q < x,q = hx,0 < h < 1 0 1 + t 1+ q 0 1+ q 2k +1

Anwendungen:

p 1 1 1 4-= arctan1 = 1- 3 + 5 - 7± ...

2 3 sum oo k+1 ln(1+ x) = x- x- + x- ±...= (-1)k x---f¨ur - 1 < x < 1 2 3 k=0 k +1

sum oo k-xk+1- g(x) = (-1) k + 1 k=0

' sum oo k k 1 |x|< 1 : g(x) = (-1) x = 1+-x-= D (ln(1+ x)) k=0

==> g(x)- ln(1+ x) = const. f¨ur - 1 < x < 1

==> g(0) - ln1 = 0

[next] [prev] [prev-tail] [front] [up]