

 ,
, 
 ,
,  sei gegebene Funktion, die stetig ist.
sei gegebene Funktion, die stetig ist.



 ,
, 

 ist ein komplexer Vektorraum.
ist ein komplexer Vektorraum.
 . Dann gilt:
. Dann gilt:

Man erhält alle Lösungen von  , indem man zu einer Lösung
, indem man zu einer Lösung  alle
Lösungen aus
alle
Lösungen aus  addiert.
addiert.
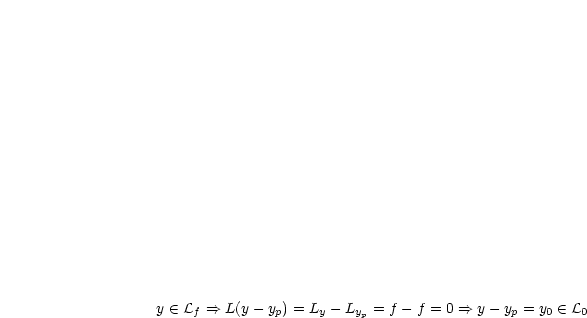
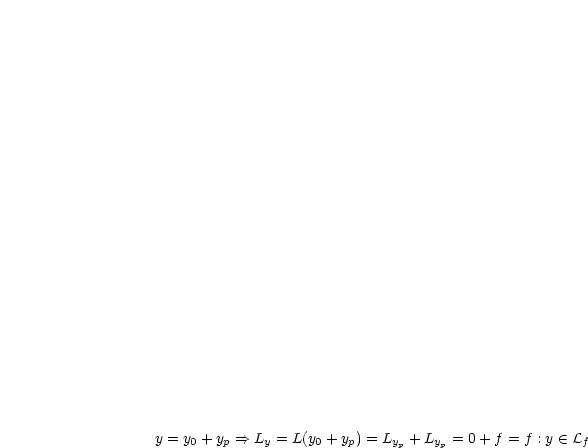

Wir verwenden den Ansatz  .
.  sei somit eine Lösung dieser
Differentialgleichung. Wenn wir diesen Ansatz in die Differentialgleichung einsetzen
und umformen, erhalten wir:
sei somit eine Lösung dieser
Differentialgleichung. Wenn wir diesen Ansatz in die Differentialgleichung einsetzen
und umformen, erhalten wir:

Mit  erhält man:
erhält man:

 Lösung von (2), so ist
Lösung von (2), so ist  Lösung von (1).
Lösung von (1).
 Lösung von (1), so ist
Lösung von (1), so ist  Lösung von (2).
Lösung von (2).
Ab jetzt:
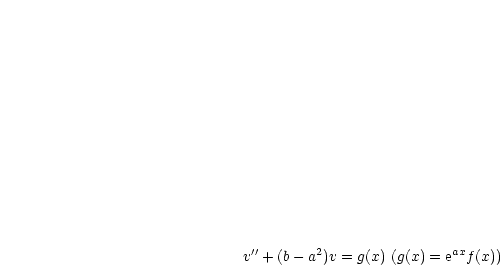
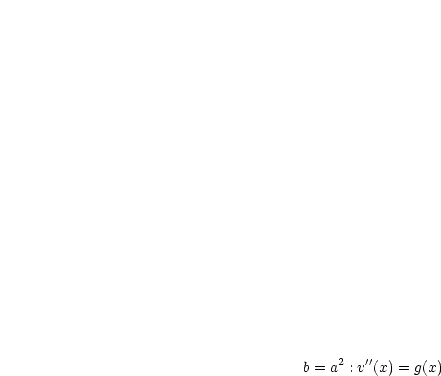
Jetzt müssen wir nur noch zweimal integrieren:


Wir integrieren partiell:


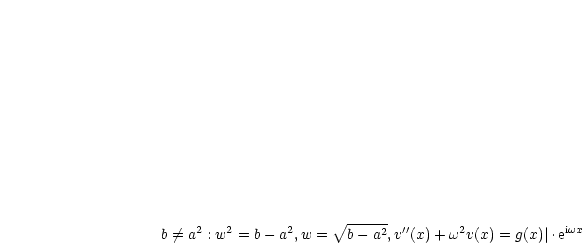





Wir subtrahieren die beiden Gleichungen voneinander:


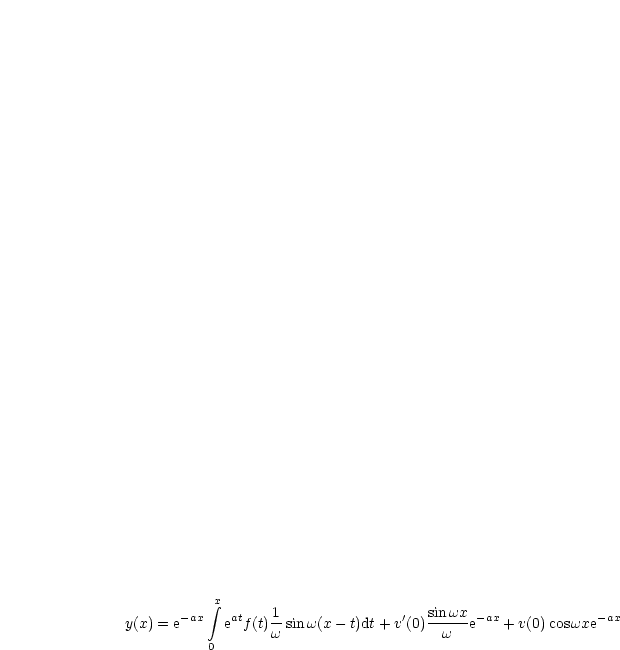
Allgemeine Lösung  ,
,  ist beliebig, aber konstant.
ist beliebig, aber konstant.
 ,
,  :
:

 ,
,  ,
, 

 | (10.2) |



 ,
,  sind nun zu berechnen.
sind nun zu berechnen.
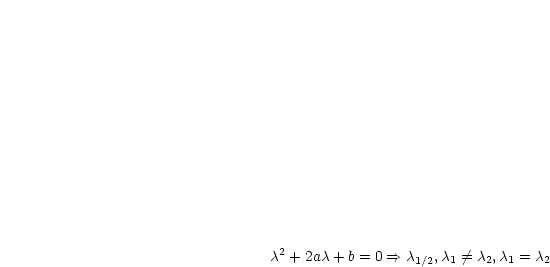
Eine alternative Variante, die stets funktioniert, ist folgende:




Dies ist eine lineare Differentialgleichung  -ter Ordnung mit konstanten
Koeffizienten.
-ter Ordnung mit konstanten
Koeffizienten.

Gilt  , so spricht man von homogenen Differentialgleichungen, sonst von
inhomogen.
, so spricht man von homogenen Differentialgleichungen, sonst von
inhomogen.

 Lösung mit speziellem Ansatz, um Problem auf bekannte Differentialgleichungen
zurückzuführen.
Lösung mit speziellem Ansatz, um Problem auf bekannte Differentialgleichungen
zurückzuführen.
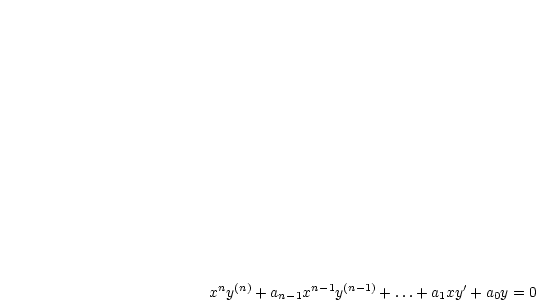
 -te Ordnung, Koeffizienten
nicht konstant
-te Ordnung, Koeffizienten
nicht konstant
Sind  und
und  zwei Lösungen einer linearen Differentialgleichung, so löst auch
zwei Lösungen einer linearen Differentialgleichung, so löst auch
 die Differentialgleichung.
die Differentialgleichung.
 ist eine nichtlineare inhomogene Differentialgleichung 1.Ordnung. Wir
verwenden zur Lösung den Ansatz:
ist eine nichtlineare inhomogene Differentialgleichung 1.Ordnung. Wir
verwenden zur Lösung den Ansatz:


Durch Einsetzen in die Differentialgleichung folgt:









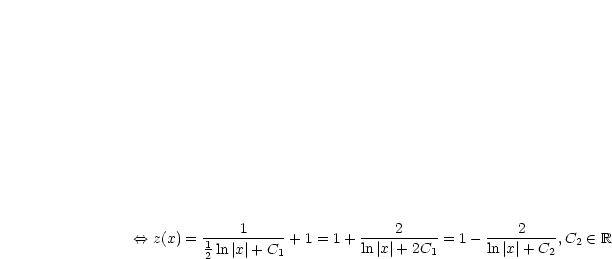
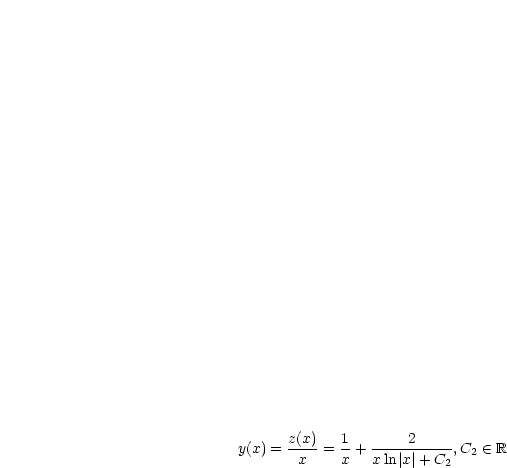
 bzw.
bzw.  löst Differentialgleichung ebenfalls. Dies ist in unserer Lösung
für
löst Differentialgleichung ebenfalls. Dies ist in unserer Lösung
für  erhalten.
erhalten.
Man löse folgende Differentialgleichung:

Wir machen folgende Substitution:

Damit gilt:

Durch Einsetzen folgt:
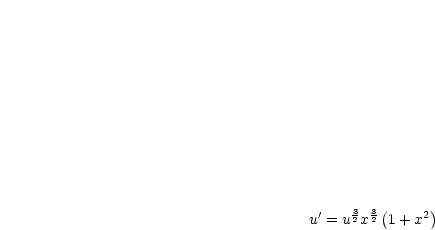
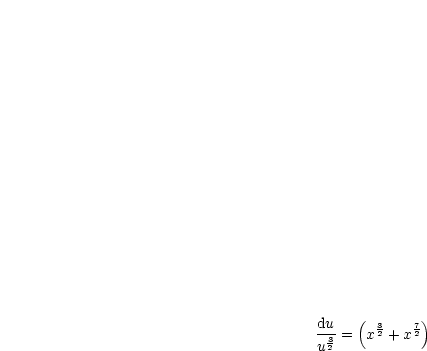
Durch Integration gilt dann:



Also erhalten wir für  :
:


Dies ist eine EULERsche Differentialgleichung.
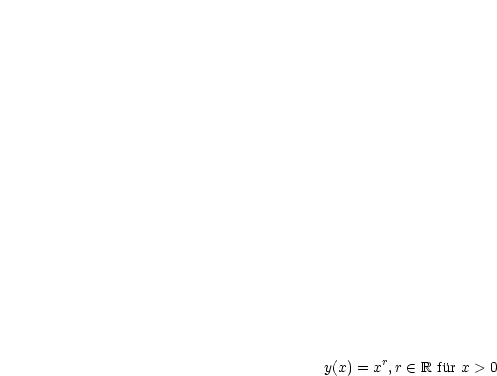

Wir verwenden folgende Substitution:


Damit folgt:


Einsetzen in die Differentialgleichung liefert:


Man verwendet hier den Ansatz 

 ,
,  .
.

Damit erhalten wir das Charakteristische Polynom:


Alle Lösungen der homogenen Differentialgleichung:

Betrachten wir nun die Differentialgleichung  . Deren Störfunktion ist
. Deren Störfunktion ist
 ; dies ist ein Polynom 1.Grades. Außerdem liegt keine Resonanz vor.
Damit verwenden wir als Ansatz zur Lösung des inhomogenen Problems
; dies ist ein Polynom 1.Grades. Außerdem liegt keine Resonanz vor.
Damit verwenden wir als Ansatz zur Lösung des inhomogenen Problems
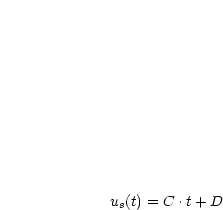 , also ebenfalls ein Polynom 1.Grades (
, also ebenfalls ein Polynom 1.Grades ( ). Durch Einsetzen
folgt:
). Durch Einsetzen
folgt:
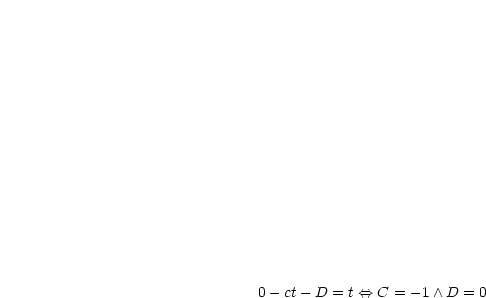
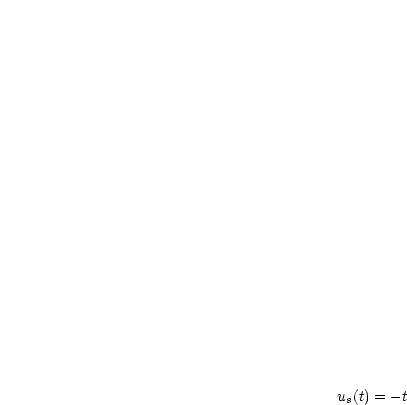
Die Differentialgleichung ist linear; die Gesamtlösung ergibt sich durch Superposition der Lösung der homogenen und der inhomogenen Gleichung:



