 :
:  ,
,  ,
,  .
.  heißt
heißt  -periodisch, falls gilt:
-periodisch, falls gilt:


 .
.
Wir betrachten  :
:  ,
,  ,
,  .
.  heißt
heißt  -periodisch, falls gilt:
-periodisch, falls gilt:


 .
.


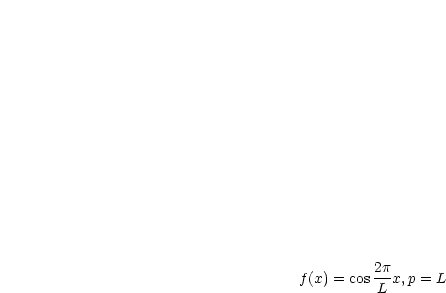
 ist nicht periodisch.
ist nicht periodisch.
Ist   -periodisch, so gilt: -periodisch, so gilt:    für jedes für jedes  . . |


Daraus folgt dann ohne Beschränkung der Allgemeinheit  .
.

Gegeben ist  ,
,  . Es sei
. Es sei  . Gesucht ist die
. Gesucht ist die  -periodische
Fortsetzung von
-periodische
Fortsetzung von  auf ganz
auf ganz  :
:
![f : R '--> C, f(x+ p) = f(x) A x, f[a,b] = f](ma45x.gif)
Gegeben ist außerdem  :
:  .
.
![U
R = (a + kp,b- kp]
k (- Z](ma48x.gif)
Bestimme  mit
mit ![x (- (a- kp,b+ kp]](ma50x.gif) mit
mit 


 -periodische Fortsetzung von
-periodische Fortsetzung von  ,
, 
 -periodische Fortsetzung von
-periodische Fortsetzung von  ,
, 
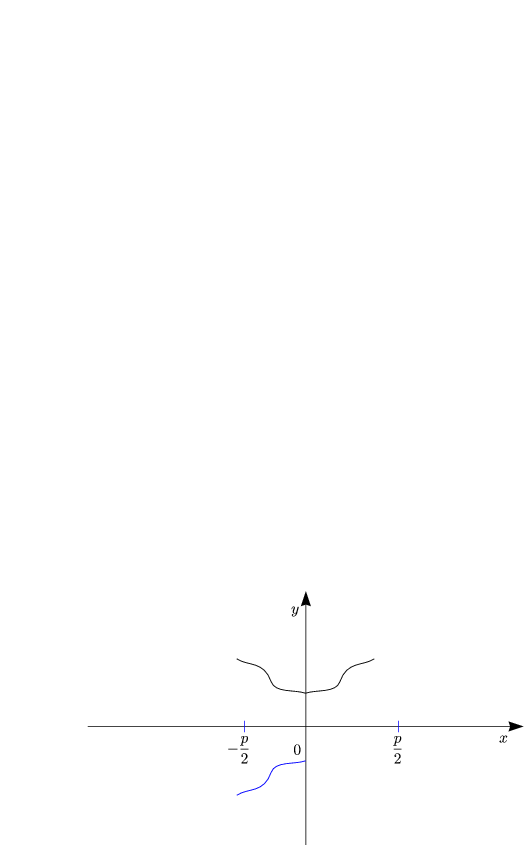
 : :  sei sei  -periodisch und integrierbar, -periodisch und integrierbar,  sei beliebig. Dann gelten: sei beliebig. Dann gelten: |
 |
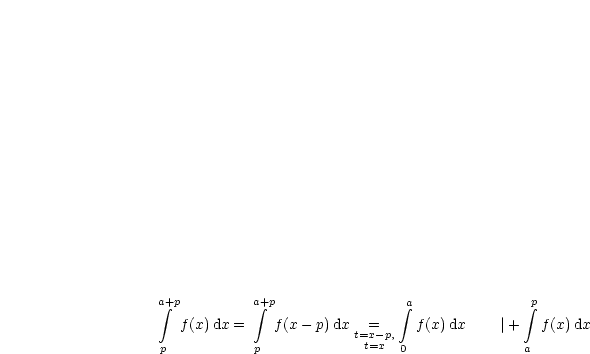

Wir ersetzen 0 durch  und
und  durch
durch  , womit folgt:
, womit folgt:

|
|

Es sei  ,
,  ,
,  -periodisch,
-periodisch,  . Dann ist
. Dann ist  für
für

 -periodisch.
-periodisch.
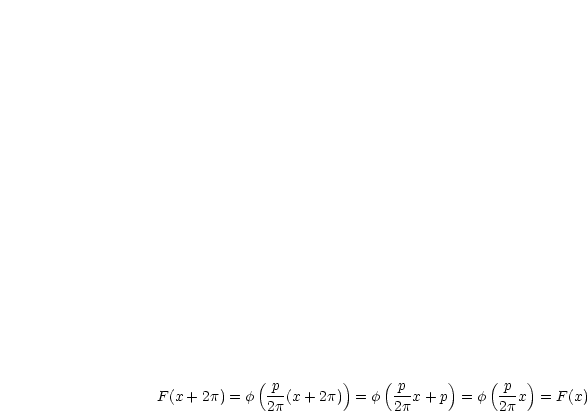
Ist 
 -periodisch, so ist
-periodisch, so ist 
 -periodisch.
-periodisch.
 sei
sei  -periodisch. Rechne nun in Periode
-periodisch. Rechne nun in Periode  . Wir betrachten
. Wir betrachten  -periodische
Funktionen auf dem Grundintervall
-periodische
Funktionen auf dem Grundintervall ![(- p,+p]](ma97x.gif) .
.