1.2 Trigonometrische Reihe

Es sei $n (- N$ : $n sum sn(x) = ckeikx k=-n$ heißt trigonometrisches Polynom ( $2p$ -periodisch). Bemerkung:

eikx=coskx+isinkx mit ck (- C

Dies sind die Partialsummen für die trigonometrische Reihe:

k sum = oo ikx sum n ikx ikx ( ix)k s(x) = cke := nl'-->imo o cke ,e = e k=- oo -n

Wir rechnen die in $sin$ - und $cos$ -Polynome um:

ikx e = coskx+ isin kx

e-ikx = coskx - isinkx

n sum ikx sum n ( ikx -ikx) sum n sn(x) = cke = c0 + cke + c-ke = c0 + [(ck + c-k)coskx+ i(ck- c-k)sin kx] = k=-n n k=1 k=1 = a0 + sum (a coskx + b sin kx) 2 k=1 k k

(1.1)

a0 = 2c0,ak = ck + c-k,bk = i(ck- c-k) f¨ur k = 1, 2, ...

c0 = a0,ck = 1(ak- ibk),c-k = 1 (ak + ibk) f¨ur k = 1, 2, ... 2 2 2

Folgerung:

--- sn(x) (- R <==> ak,bk (- R <==> ck = c- k

Aus $ak$ , $bk (- R$ ergibt sich $--- ck = c-k$ , $-- c-k = ck$ . Mit $--- ck = c- k$ gilt wiederum:

|----------------------------------------------| ak-=-ck +-ck (- -R-und-bk =-i(ck--ck) =-i.(2iIm)ck- (- R

Erinnerung:

oo sum k 1- (k) akx = f (x) mit ak = k!f (0) k=0

Lemma:

$k$ , $l (- Z$ . Dann gilt:

$integral +p + integral p { 2p : k = l eikxe-ilxdx = ei(k-l)xdx = 1 ( i(k-l)p -i(k-l)p) i(k---l) e - e = 0 -p -p$

$k /= l$ , $e2nip = 1$ , $einp = e- inp$

Lemma:

Für $k$ , $l (- N U {0}$ gelten:

$integral p sinkxcoslxdx = 0 - p$
$integral p integral p sinkxsinlxdx = coskx coslxdx = pdkl - p - p$

Es sei $k = 0$ , 1, 2, $...$ :

1 integral +p sum n 1 integral +p sum n 2p- sn(x)e-ikx dx = cl2p- eilxe-ikxdx = cldkl = ck -p l=-n ---p- ----- l= -n dkl

integral +p ck = 1-- sn(x)e-ikxdx(k = -n,- n+ 1,...,n) 2p -p

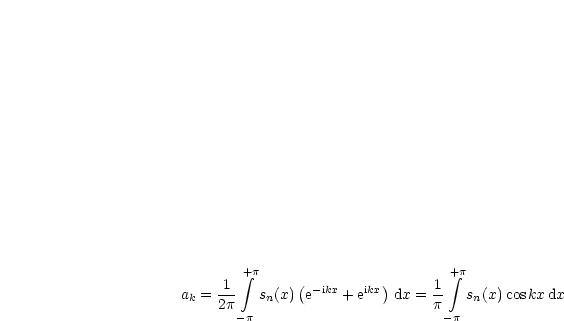
+ integral p + integral p ak =-1- sn(x)(e-ikx + eikx)dx = 1- sn(x)coskx dx 2p p -p - p

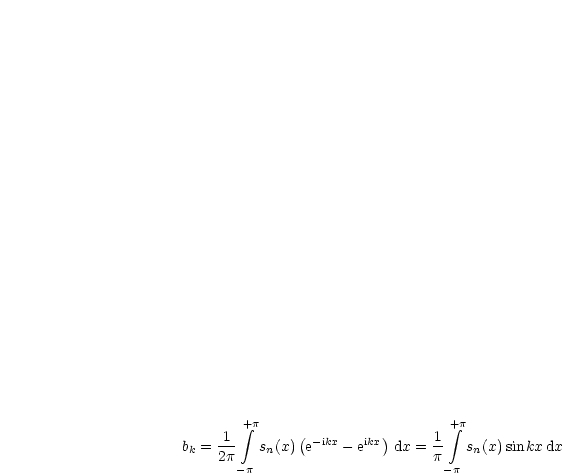
+p +p -1- integral ( -ikx ikx) 1- integral bk = 2p sn(x) e - e dx = p sn(x)sin kxdx -p -p

Satz:

Jedes trigonometrisches Polynom $sum n ikx a0 sum n sn(x) = cke = 2 + (ak coskx + bksin kx) l=-n k=1$ definiert eine auf $R$ stetige und $2p$ -periodische Funktion. Es gelten für $k (- N U {0}$ :

$+ integral p ck =-1- sn(x)e-ikxdx 2p -p$
$1 integral +p ak =-- sn(x)coskx dx p -p$
$1 + integral p bk =-- sn(x)sinkxdx p -p$

Satz:

Konvergiert die Reihe $+ sum oo ckeikx - oo$ gleichmäßig auf $[-p,+p]$ gegen die Funktion $f$ , so gelten:

$f$ ist $2p$ -periodisch und stetig.
$integral +p ck =-1- f(x)e-ikxdx 2p -p$ , $k (- Z$

Begründung:

$f$ ist stetig: $f (x) = lim sn(x) n'--> oo stetig$ ist stetig, da gleichmäßige Konvergenz vorliegt.

f(x+ 2p) = lim sn(x+ 2p) = lim sn(x) = f(x) n'--> oo n'-->o o

+ integral p + integral p( ) + integral p -1- f(x)e-ikx = 1-- lim sn(x) e-ikxdx = lim -1- sn(x)e-ikxdx = ck 2p-p 2p-p n'-->o o n'--> oo 2p- p

FOURIERreihen:

Stückweise stetig:
$f$ heißt stückweise stetig, falls es höchstens endlich viele Unstetigkeiten $x 1$ , $x 2$ , $...$ , $x n$ gibt, wobei
$xl'-->imxj-f (x) =: f(xj- )$ und $x'-->lixmj+ f(x) =: f(xj+)$ existieren. Betrachten wir folgendes Beispiel:
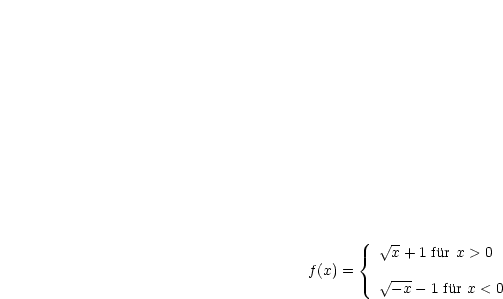
$V~ -- { x +1 f¨ur x > 0 f(x) = V~ --- -x - 1 f¨ur x < 0$

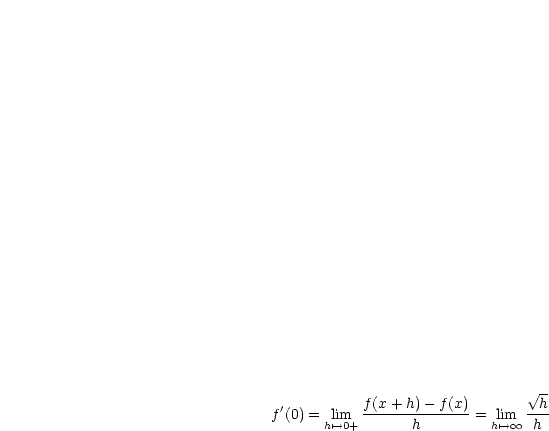
$f(x + h)- f(x) V~ h- f'(0) = lhi'-->m0+ ------h------= hl'-->imo o -h-$
Es sei $f$ stückweise $2p$ -periodisch.
Stückweise glatt:
$f$ heißt stückweise glatt, falls es endlich viele Unstetigkeiten $x1$ , $x2$ , $...$ , $xn$ gibt mit:
- $f(xj-)$ , $f(xj+)$ existieren.
- $f'(xj-)$ , $f'(xj+)$ existieren.
Dies soll gelten für $j = 1$ , 2, $...$ , $n$ .

FOURIERkoeffizient von $f$ : $1 + integral p --- f(x)e-ikx dx = f^(k) mit k (- Z 2p- p$
FOURIERpolynom von $f$ : $n sum ^ ikx f(k)e = Fnf (x) k= -n$
FOURIERreihe von $f$ : $sum oo ^ ikx f(k)e = nli'-->mo o Fnf(x) =: Ff(x) k=- oo$

Es bestehen nun folgende Zusammenhänge:

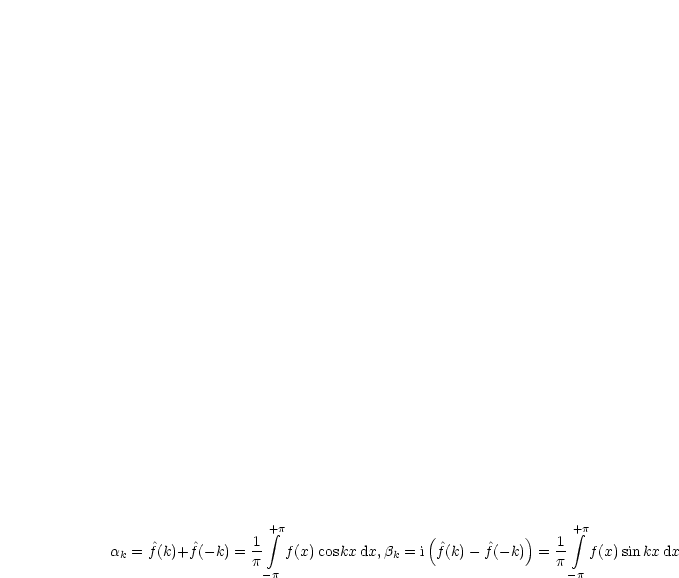
integral +p ( ) integral +p a = f^(k)+ ^f(-k) = 1- f(x)coskxdx,b = i ^f(k) - ^f(- k) = 1- f(x)sinkx dx k p k p -p -p

Bemerkung:

Ist $f$ gerade, so gelten $fk = 0$ $A$ $k$ . $oo Ff(x) = a0-+ sum akcoskx 2 k=1$

$+ integral p b = 1- f(x)sinkx dx = 0 k p --- --- - p gerade$

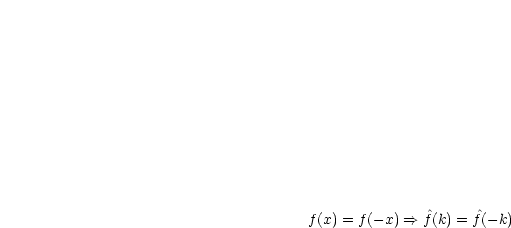
$f(x) = f(-x) ==> ^f(k) = f^(-k)$
Ist $f$ ungerade, so gelten $ak = 0$ $A$ $k$ . $f(x) = - f(-x) ==> ^f(k) = - ^f(- k)$
$Ff$ ist eine reine Sinusreihe.

Beispiel:

Es sei $2 g(x) = x$ für $- p < x < p$ . Wir wollen die Funktion $2p$ -periodisch fortsetzen zu $f$ : $f[-p,p] = g$ . Wir suchen die zugehörige FOURIERreihe:

integral p ^f(k) =-1- x2e-ikxx dx mit k (- Z 2p - p

^ p2- f(0) = 3

2 ^f(k) = (-1)k-2 mit k /= 0 k

a0- sum oo p2- sum oo k-4 Ff(x) = 2 + ak coskx = 3 + (-1) k2 coskx k=1 k=1

Hierbei handelt es sich um die Darstellung von $g(x) = x2$ auf $[-p,+p]$ . Die Reihe ist gleichmäßig konvergent.

Problem:

Für welche $f$ konvergiert $Ff$ ?
Für welche $f$ gilt $f = Ff$ und für welche $x$ gilt $f(x) = Ff (x)$ ?

Satz:

Es gelte $oo sum ikx f(x) = gke k=- oo$ und die Konvergenz ist gleichmäßig. Dann gilt: $f(x) = Ff (x)$ $A$ $x$ . („Eine gleichmäßige konvergente trigonometrische Reihe ist die FOURIERreihe der durch sie dargestellten Funktion.“)

Zur Begründung betrachten wir folgendes:

Satz:

|-------------------------------------| | sum + oo ikx | gk = ^f(k) ==> f(x) = ^f(k)e = Ff (x) | ------------------k=-- oo ----------------

Satz:

$f$ sei $2p$ -periodisch, stetig und $Ff$ konvergiere gleichmäßig auf $[-p,+p]$ . Dann gilt: $Ff(x) = f(x)$ , $x (- R$ .

Beispiel:

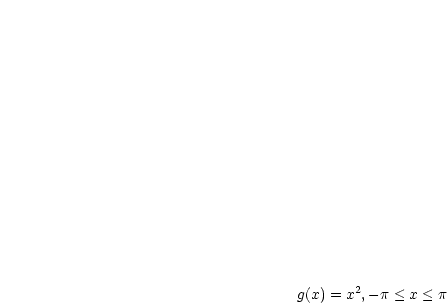
g(x) = x2,- p < x < p

$2p$ -periodische Fortsetzung von $f$ erstellen. Da $f$ stetig ist, ist $Ff$ gleichmäßig konvergent. Damit folgt:

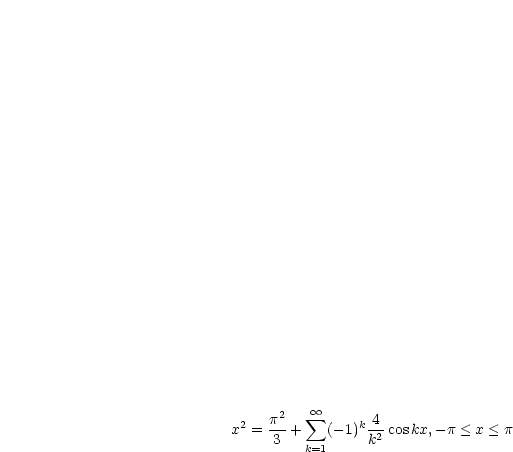
2 p2 sum oo k 4 x = 3-+ (-1) k2 coskx,- p < x < p k=1

Stelle $x = 0$ : $2 sum oo p--= (- 1)k+1 1- 12 k=1 k2$
Stelle $x = p$ : $2 sum oo p--= -12 6 k=1k$
$x '--> q$ : $x = q - p,-p < x < p <==> 0 < q < 2p$

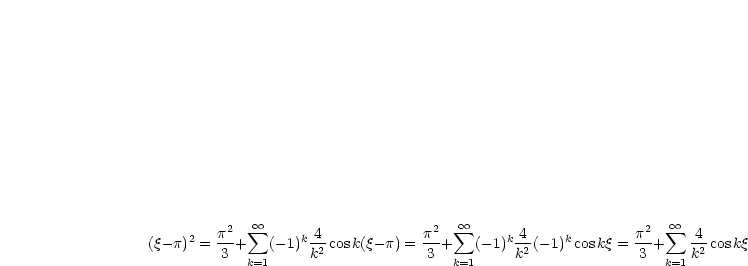
$2 p2- sum oo k 4 p2- oo sum k 4- k p2- sum oo -4 (q- p) = 3 + (- 1) k2 cosk(q-p) = 3 + (- 1) k2(- 1) coskq = 3 + k2 coskq k=1 k=1 k=1$
Damit erhalten wir beispielsweise:
$|-----------------------------------------| | sum oo 1 (x - p)2 p2 | | -2 cos(kx) = ----- - ---f¨ur 0 < x < 2p -k=1k--------------2-------12--------------$

$|------2---2---- oo -------------------| |(x---p)-- p--= sum coskx-f¨ur 0 < x < 2p | 4 12 k=1 k2 | --------------------------------------$

Übung:

2 g(x) = t(x - p),0 < x < 2p

[next] [prev] [prev-tail] [front] [up]