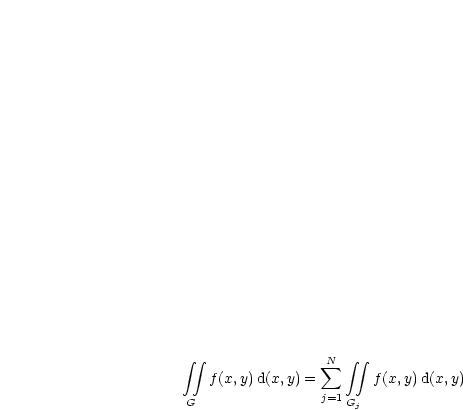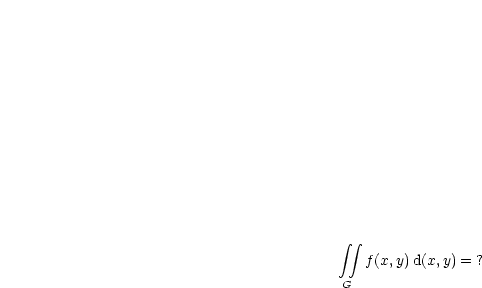
 sei offen, zusammenhängend und
sei offen, zusammenhängend und  . „Zusammenhängend“
bedeutet, daß mit 2 Punkten von
. „Zusammenhängend“
bedeutet, daß mit 2 Punkten von  auch eine Verbindungskurve ganz in
auch eine Verbindungskurve ganz in
 . Zwei getrennte Mengen sind beispielsweise nicht zusammenhängend.
Die Menge darf aber „Löcher“ besitzen. Wenn keine Löcher vorhanden
sind, spricht man von „einfach zusammenhängend“. Eine offene und
zusammenhängende Menge heißt Gebiet.
. Zwei getrennte Mengen sind beispielsweise nicht zusammenhängend.
Die Menge darf aber „Löcher“ besitzen. Wenn keine Löcher vorhanden
sind, spricht man von „einfach zusammenhängend“. Eine offene und
zusammenhängende Menge heißt Gebiet.
 ist außerdem beschränkt, das heißt es gibt eine Zahl
ist außerdem beschränkt, das heißt es gibt eine Zahl  mit
mit
 für die gilt
für die gilt  (
( ).
).  :
:  sei
stetig, also gelte
sei
stetig, also gelte  . Mit
. Mit  bezeichnen wir
bezeichnen wir  mit
Rand. Folgendes können wir beispielsweise noch nicht integrieren:
mit
Rand. Folgendes können wir beispielsweise noch nicht integrieren:

Im  ist eine Linie kein Gebiet.
ist eine Linie kein Gebiet.
Voraussetzung:
 ist beschränktes Gebiet:
ist beschränktes Gebiet:  (
(
 ist beschränkt.)
ist beschränkt.)
Definition:
Definition von  für spezielle für spezielle  : : |
In  -Richtung projizierbare Gebiete: -Richtung projizierbare Gebiete:  |
 |
Bemerkungen:
 . Dann bedeutet:
. Dann bedeutet:


- Für
 ist
ist  Flächeninhalt von
Flächeninhalt von
 .
.

|
Beispiel:
 sei der beschränkte Teil des
sei der beschränkte Teil des  , der durch die Kurve
, der durch die Kurve  berandet wird. Wir wollen nun berechnen:
berandet wird. Wir wollen nun berechnen:



Alternative:
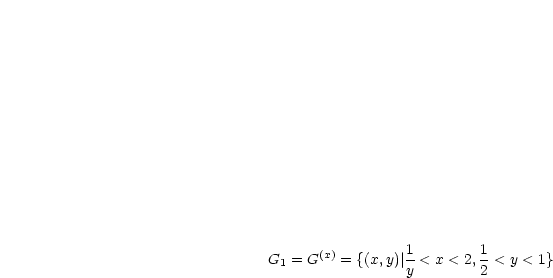
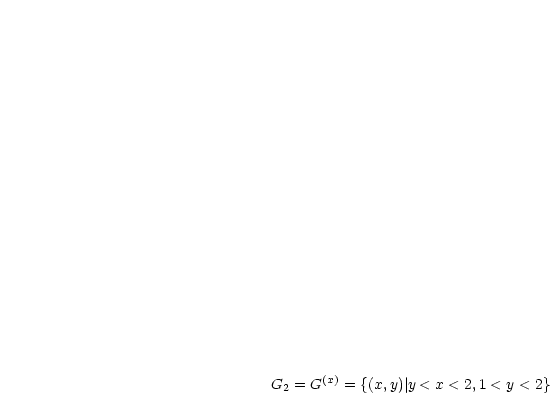
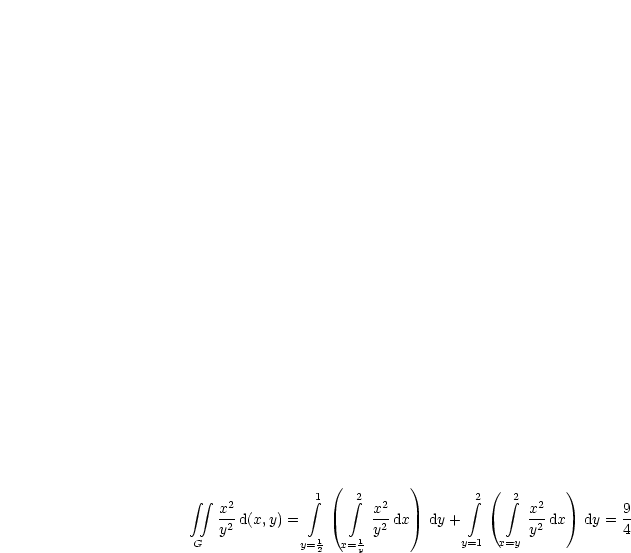
Beispiel:



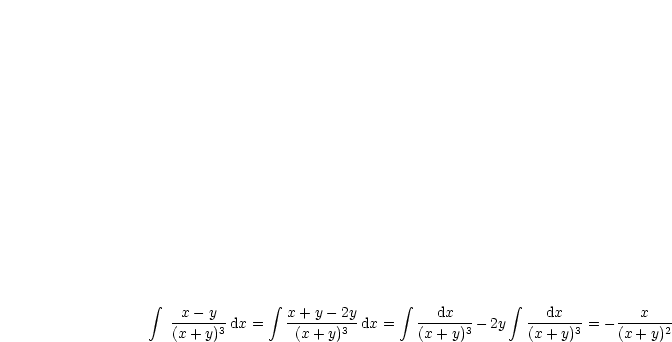

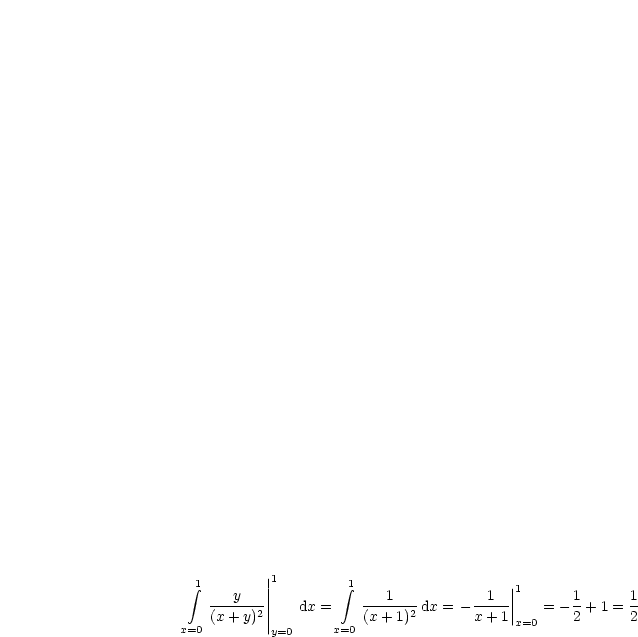

Dies liefert unterschiedliche Ergebnisse, da  .
.  existiert nicht.
existiert nicht.


Beispiel:
![y2+1
integral 1 integral 2 integral 1 [1 3 ]y2+1 integral 1(1 ( 2 )3 1 4) [1 ( 2 )4 1 5]1
I = x ydx dy = 3x y dy = 3 y + 1 y - 3y dy = 24 y + 1 - 15 y =
0 y 0 y 0 0
1 1 1 |67-|
= -- .16- -- .1- -- = |---|
24 15 24 -120-](ma3211x.gif) | (4.1) |
Beispiel:

Für das erste Integral folgt:
![1x2 1 1
integral integral integral [ 2]x2 integral 5 [1 6]1 1
I1 = 2xydy dx = xy 0 dx = x dx = 6x = 6
0 0 0 0 0](ma3213x.gif)
![integral 2 x integral 2 integral 2 [ ] 2 integral 2( ) integral 2( )
I2 = 2xydy dx = xy2 x4x-4 dx = x5 - x(4x- 4)2 dx = x5 - 16x3 + 32x2- 16x dx =
1 4x-4 1 1 1
[ ]2
= 1x6 -4x4 + 32x3- 8x2 = 11
6 3 1 6](ma3214x.gif) | (4.2) |
Durch Addition gilt dann:

 -Richtung projizierbare Gebiete:
-Richtung projizierbare Gebiete: 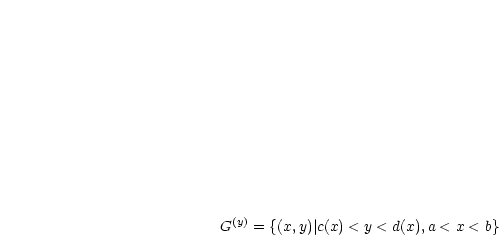

 disjunkt in Teilgebiete
disjunkt in Teilgebiete  der Formen (1),(2) zerlegen, wobei
der Formen (1),(2) zerlegen, wobei  höchstens Randstücke gemeinsam haben, so wird definiert:
höchstens Randstücke gemeinsam haben, so wird definiert: