[next] [prev] [prev-tail] [tail] [up]

4.2 Vertauschen der Integrationsreihenfolge

Satz:

Es sei -- G = {[a,b]×[c,d]} und -- f (- C0(G) . Dann gilt:
( ) ( ) integral b integral d integral d integral b f(x,y)dy dx = f(x,y)dx dy x=a y=c y=c x=a

Beispiel:
G = {(x,y)| 1 < x2 + y2 < 4}

integral integral I(G) = d(x,y) G

I(G) = 4 (I(G1) +I(G2))

( ---- ) integral 1 V~ integral 4- x2 I(G1) = dy dx = 1 V~ 3 + p V~ ---- 2 12 x=0 y= 1- x2

( ) integral 2 V~ 4- integral -x2 I(G2) = dy dx = -1 V~ 3 + 2p 2 3 x=1 y=0

G = {(r,f)|1 < r < 2,0 < f < 2p}

Wir können ein Integral approximieren durch eine Summe:

integral integral sum N sum M f(x,y)d(x,y) ~ f(pjk)Djk G j=0k=0

Problem:

Wir wollen den Flächeninhalt des Gebietes G berechnen. Deshalb führen wir eine Koordinatentransformation * * F : G '--> G,F (G ) = G durch: F soll injektiv und stetig differenzierbar sein.

detF (u,v) /= 0

Wir approximieren den Flächeninhalt:

I(Q) ~ ||a× b||

a = F(u +Du, v)- F (u,v) = D1F(u,v)Du + o(| Du |)

b = F(u,v+ Dv) - F (u,v) = D2F (u,v)Dv + o(| Dv|)

D F (u,v),D F (u,v)] = F '(u,v) = J (u,v) :||a×b||~ ||D F(u,v)× D F (u,v)|| DuDv 1 2 F --1------ --2------ detF'(u,v)

integral integral integral integral d(x,y) = det(F '(u,v)d(u,v) F(G*)=G G*

Beispiel:

Wir verwenden Polarkoordinaten u = r und v = f :

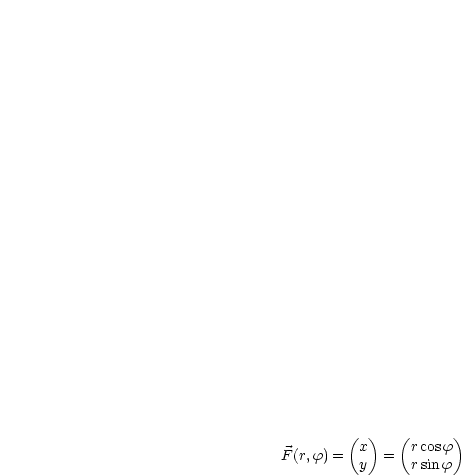
( ) ( ) F (r,f) = x = r cosf y r sinf

' detF (r,f) = r

integral integral integral 2p integral 2 d(x,y) = rdrdf = 3p G f=0 r=?1

d(x,y) = |detF '(u,v)| d(u,v)

Flächenelement in (x,y) -Koordinaten <==> Flächenelement in (u,v) -Koordinaten (Flächenelement in Polarkoordinaten) r drdf

integral integral integral integral t=g(t) integral integral integral integral I(G) = dF = d(x,y) = rdr df = |detF'(u,v)|d(u,v) G x,y r,f u,v

[next] [prev] [prev-tail] [front] [up]