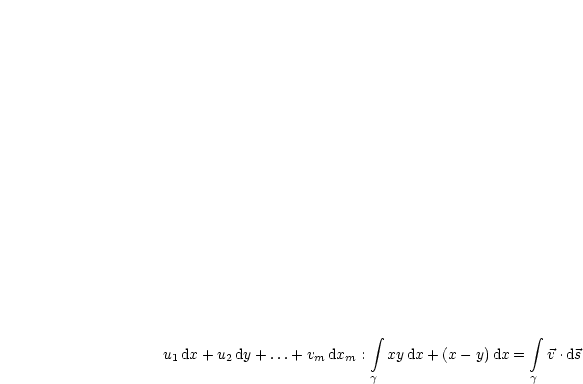|
|
|
|
|
|
|
|
|
|
 .
.


 ist eine Parametertransformation mit
ist eine Parametertransformation mit  :
: ![[a,b] '--> [a,b]](ma3262x.gif) und
und
 .
.
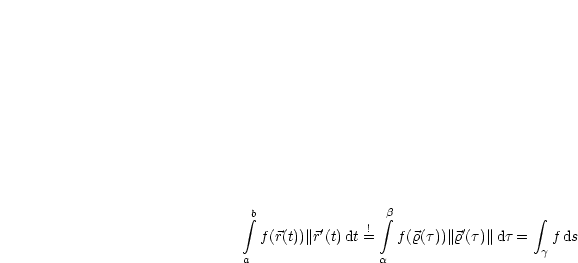
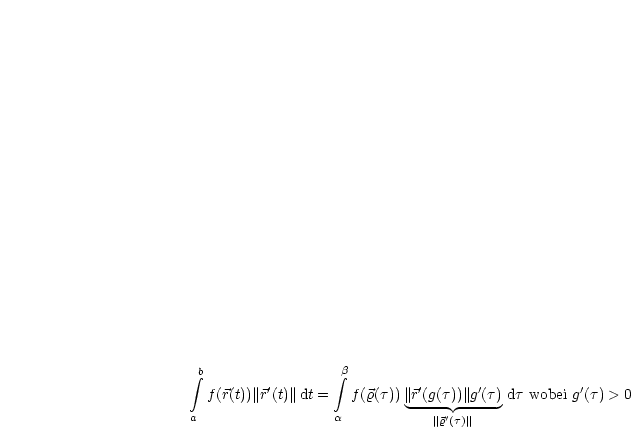




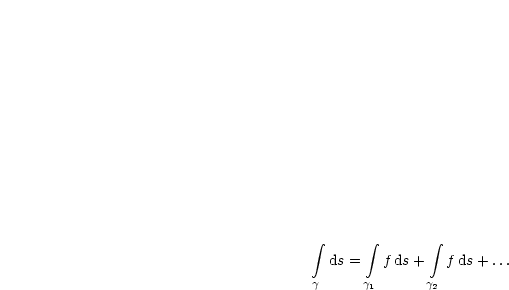
 eine geschlossene Kurve ist, kann man ein sogenanntes Ringintegral
definieren:
eine geschlossene Kurve ist, kann man ein sogenanntes Ringintegral
definieren:

 sei JORDANkurve, das heißt
sei JORDANkurve, das heißt  ist injektiv (besitzt keine
Doppelpunkte).
ist injektiv (besitzt keine
Doppelpunkte).
 über eine Kurve
über eine Kurve 
|
|
|
|
|

 sei Vektor der Länge Eins in Richtung
sei Vektor der Länge Eins in Richtung  . Wir können den
Integralbegriff somit erweitern, indem wir nun für das Integral über ein Skalarfeld
schreiben können:
. Wir können den
Integralbegriff somit erweitern, indem wir nun für das Integral über ein Skalarfeld
schreiben können:
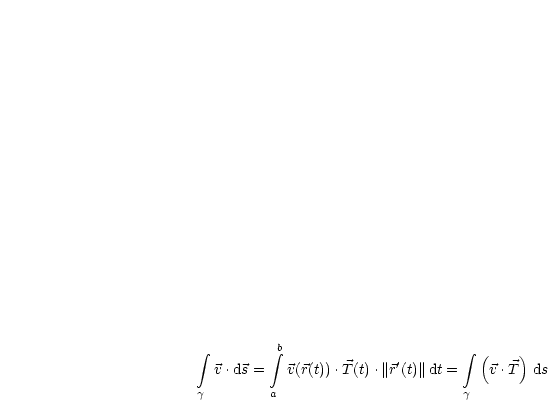
Da  ist, gilt:
ist, gilt:


Zum Merken:

 ,
, 

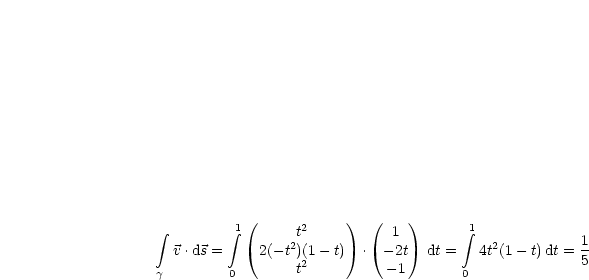






Es sei  :
:  mit
mit  und
und  .
.
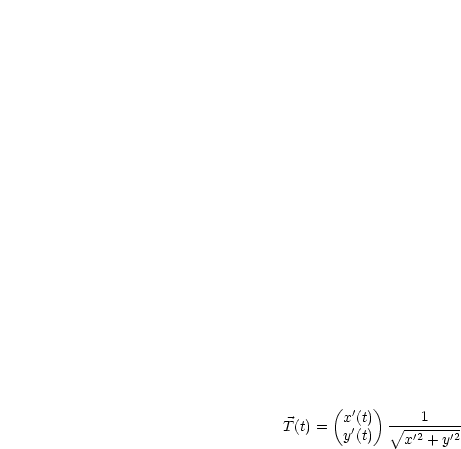



Dieses Integral nennt man Zirkulation des Vektorfeldes  längs
längs  .
.

Dies ist der sogenannte Fluß  längs
längs  .
.
Wir wollen folgendes Integral berechnen:
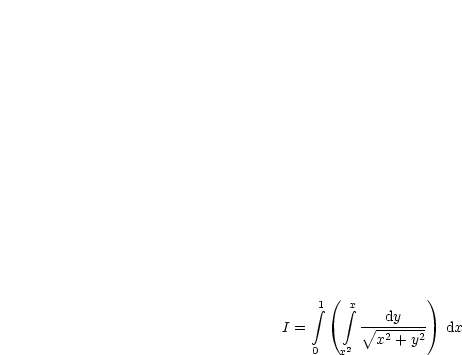
Wir wollen dies lösen, indem wir Polarkoordinaten einführen:



Es sei  ,
,  und
und  .
.  :
:  ist stetig differenzierbar:
ist stetig differenzierbar:


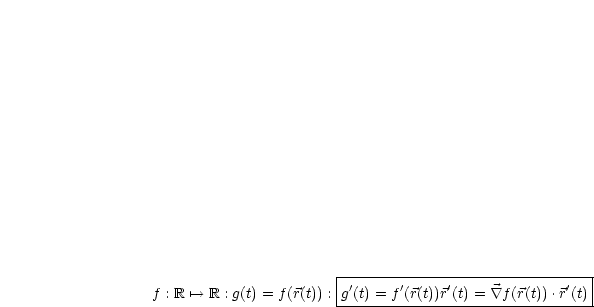
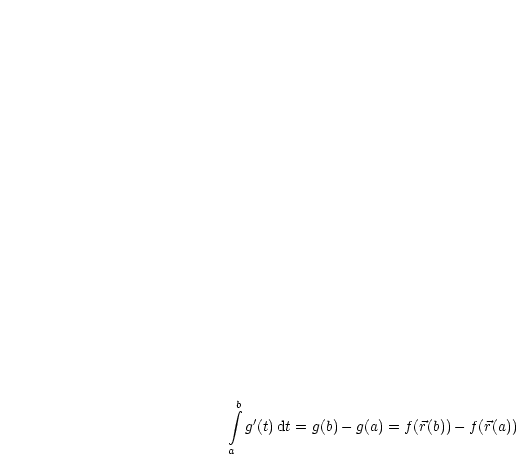

In  ist
ist  .
.

![(u(x,y)) integral integral b
v(x,y) = w(x,y) : v ds = [u(x,f(x))+ w(x,f (x))f'(x)] dx
g a](ma3330x.gif)
![(g(t)) integral integral d
r(t) = t ,c < t < d : vds = [u(g(t),t)g'(t) +w(y(t),y] dy
g c](ma3331x.gif)