4.4 Gauscher Integralsatz in der Ebene (Gauscher Satz)

4.4 GAUßscher Integralsatz in der Ebene (GAUßscher Satz)

Satz:

$G (_ R2$ sei beschränktes Gebiet. $@G$ sei positiv bezüglich $G$ orientiert und $@G$ sei stückweise glatt. $G$ sei sowohl in $x$ -Richtung als auch in $y$ -Richtung projizierbar. $G = {(x,y)|a(y) < x < b(y),c < y < d}= {(x,y)|c(x) < y < d(x),a < x < b}$ $-- P = P (x,y),Q = Q(x,y) (- C1(G)$ .

Mit $( ) v(x,y) = P(x,y) Q(x,y)$ gilt:

$gf integral integral v .ds = [D Q(x,y)- D P (x,y)] d(x,y) 1 2 @G G$

$gf integral integral (P dx+ Q dy) = [Q(x,y) - P(x,y)] d(x,y) @G G$

Beweis:

Wir schreiben:

( ) ( ) v(x,y) = P (x,y) + 0 = v1(x,y)+ v2(x,y) 0 Q(x,y)

Der 1.Schritt ist, $gf v1ds @G$ zu berechnen.

( t ) g1 : r(t) = c(t) f¨ur a < t < b

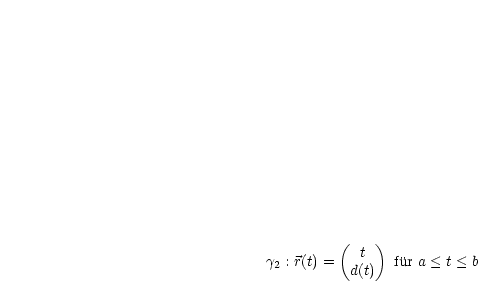
( ) t g2 : r(t) = d(t) f¨ur a < t < b

Es ist $@G = g1 + g2$ .

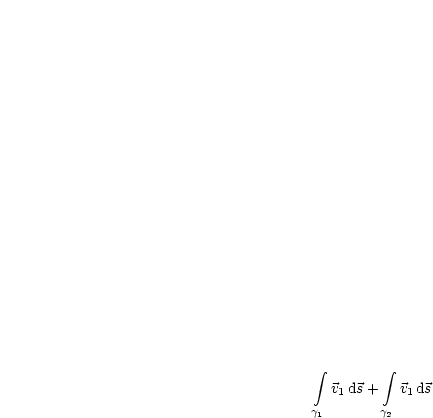
integral integral v ds+ v ds 1 1 g1 g2

b b |_ d(x) _| gf integral integral integral integral integral @Gv1.ds = [P(x,c(x)) - P(x,d(x))] dx = - |_ D2P (x,y)dy _| dx = - D2P(x,y)d(x,y) a a c(x) G

- (a(t)) g1 : r = r(t) = t f¨ur c < t < d

(b(t)) g2 : r = r(t) = t f¨ur c < t < d

gf integral i ntegral integral d integral d ( b( integral y) ) integral integral v .ds = - v .ds+ v ds = [- Q(a(y),y) +Q(b(y),y)] dy = D Q(x,y)dx dy = D Q(x,y)d(x,y) 2 2 2 1 1 @G g1 g2 c c x=c(y) G

Somit folgt nun:

| gf ------------- gf ------- integral integral --------------------------| | | | (v1 + v2) .ds = v .ds+ [D1Q(x, y)- D2P (x,y)] d(x,y) @G--------------@G--------G-----------------------------

Beispiel:

Es sei $g$ : $r = f$ für $0 < f < p$ . ( $r$ , $f$ sind Polarkoordinaten in der $(x,y)$ -Ebene.)

(x(x2 + y2)) v(x,y) = y(x2 + y2)

Gesucht ist $integral v .ds g$ .

integral integral integral integral v .ds+ v .ds= [D1Q -D2P ] d(x,y) g----- gf g1---- G v.ds @G

( ) integral integral integral 0( 3) ( ) [ ]0 4 g1 : r(t) = t ,-p < t < 0 : v.ds = - v.ds = - t .1 dt = -1 t4 = p-- 0 g g1 - p 0 0 4 -p 4

integral ( 3 ) ( 3 ) v.ds : v(r cosf, rsinf) = r3cosf = f3cosf g r sinf r=f f sinf

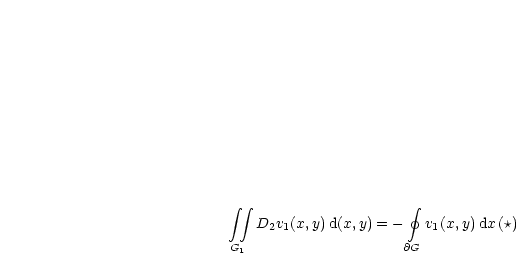
integral integral gf D v(x,y)d(x,y) = - v (x,y)dx(*) 21 1 G1 @G

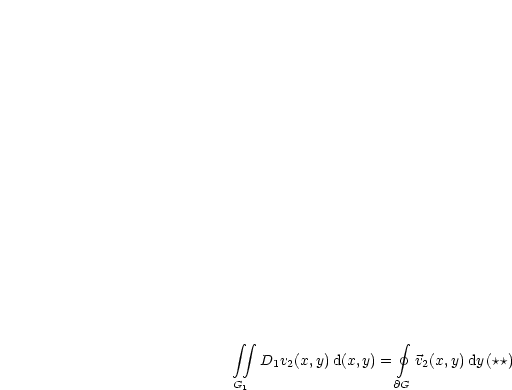
integral integral gf D1v2(x,y) d(x,y) = v2(x,y)dy (**) G1 @G

$(*)$ gilt für folgende Gebiete:

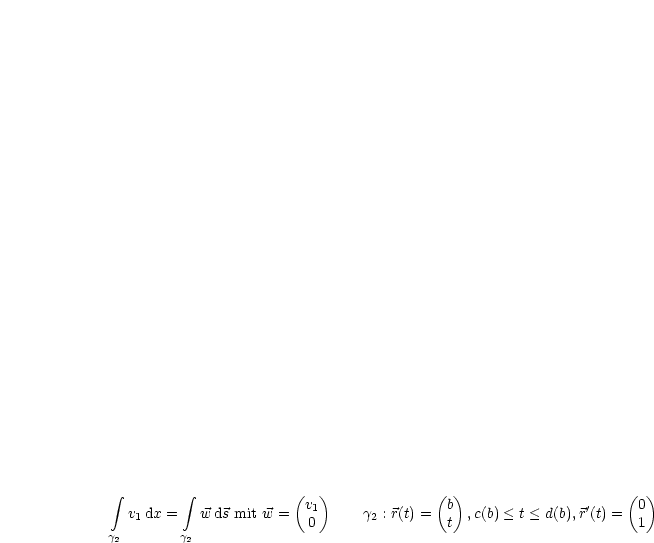
integral integral ( ) ( ) ( ) v1dx = w ds mit w = v1 g2 : r(t) = b ,c(b) < t < d(b),r'(t) = 0 0 t 1 g2 g2

integral d integral (b) v1dx = (v1(b,t).0+ 0 .1) dt = 0 g2 c(b)

( ) gf integral integral integral integral integral b d integral (x) v1dx = v1dx + v1dx + v1 dx+ v1 dx- (D2v1)(x,y)dy dx @G g1 g3 g2 g4 x=a y=c(x) ------ ------ letztesMal)

$(**)$ gilt für Gebiete, die gleichzeitig die Eigenschaften $1,2;1*,2*;1,2*;1*,2$ haben, also beispielsweise Rechtecke, Dreiecke, Ellipsen, Kompositionen aus Geraden und krummlinigen Begrenzungen.

Bemerkung:

Der Satz gilt für Gebiete, die sich in endlich viele Teilgebiete a.), b.), c.) oder d.) zerlegen lassen. Das sind im wesentlichen alle vernünftigen Gebiete.

integral integral integral integral (D1v2 - D2v1)d(x,y) = + vds G1 St¨uck von @G

integral integral integral integral (D1v2 - D2v1)d(x,y) = + vds G1 St¨uck von @G

integral integral gf integral integral D1v2 - D2v1d(x,y) = v.ds + + g g G @G 1 2

Anwendungen des GAUßschen Satzes (Raum) (GREENscher Satz (Ebene)):

(- y) v(x,y) = x

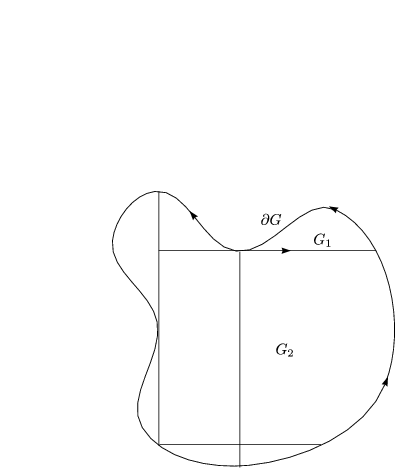
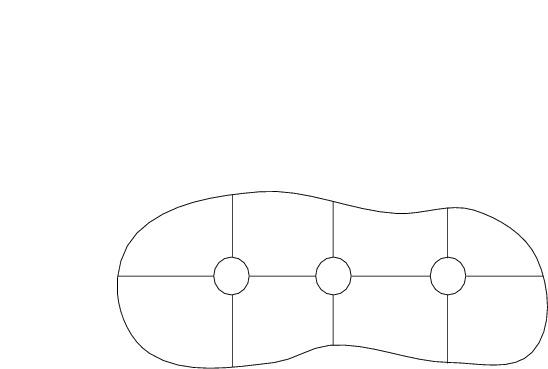
Wir müssen die Komponentenfunktionen ableiten und erhalten:

D v = 1,D v = - 1 1 2 2 1

integral integral gf 2 d(x,y) = (xdy - ydx) = 2I(G) G @G

4.4.1 LEIBNIZsche Sektorformel

$1 r = r(t) (- C [a,b]$ (stückweise), $G = {(x,y)|x = rcost,y = r sint,a < t < b,0 < r < r(t)}$ . Dann gilt:

$b 1 integral 2 I(G) = 2 r (t)dt a$

\text{[math]}

| _ _| 1 integral integral integral I(G) = - |_ + + (x dy- ydx) _| 2 g1 g2 g3

(t cosa) g1 : r1(t) = tsina f¨ur 0 < t < r(a)

( ) g3 : r3(t) = t cosb f¨ur 0 < t < r(b) t sin b

( ) v = - y x

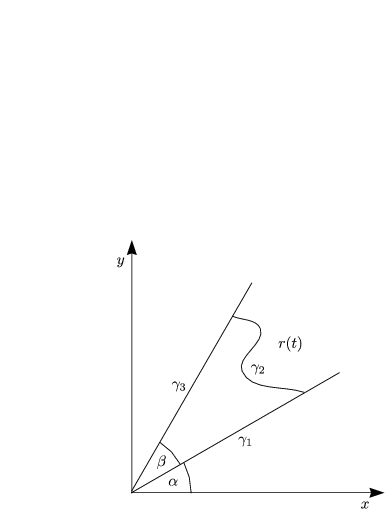
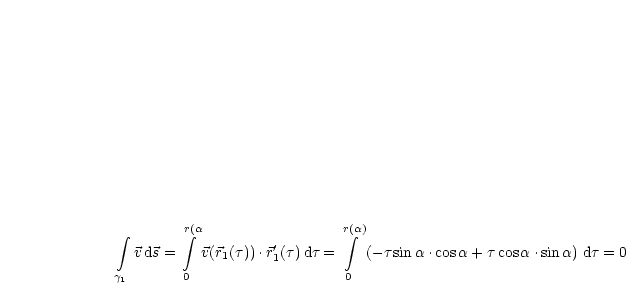
integral r integral (a r integral (a) vds = v(r1(t)).r'1(t)dt = (-t sina .cosa + t cosa .sin a) dt = 0 g1 0 0

integral v ds = 0 g3

(r(t)cost) g2 : r(t) = r(t)sint f¨ur a < t < b

' (r'(t)cost- r(t)sint) r(t) = r'(t)sint+ r(t)cost

integral integral b b integral (x dy-y dx) = [(-r(t)sint)(r'cost- rsin t)+ rcost(r'sin t+ rcost)] dt = r2(t)dt g2 a a

Beispiel: Kreisausschnitt

integral a F = 1 r2dt = 1r2a 2 2 0

4.4.2 Umschreiben des GAUßschen Satzes (STOKESscher Satz)

$G$ sei wie vorher, $v : G '--> R3$ sei stetig differenzierbar in $G-$ .

$( v(x,y)) v(x,y) = v1(x,y) v2(x,y) 3$

Dann gilt:

$integral integral ( ) gf \~/ × v(x,y) .e3 d(x,y) = v.ds G @G$

Begründung:

( ) ... \~/ × v = ... D1v2 - D2v1

Damit ist die Aussage bewiesen. Dies ist nun der sogenannte STOKESscher Satz (in der Ebene). Weiterhin formen wir um:

$( ) T = x' . V~ --1----- y' x'2 + y'2$ , $( ) N = y' . V~ --1----- - x' x'2 + y'2$

$G,@G$ sei wie vorher, $w : G '--> R2$ sei stetig differenzierbares Vektorfeld:

$( ) w1(x,y) w(x,y) = w2(x,y)$

Dann gilt:

$integral integral gf \~/ .wd(x,y) = w .N ds G @G$

Dies ist der sogenannte Divergenzsatz.

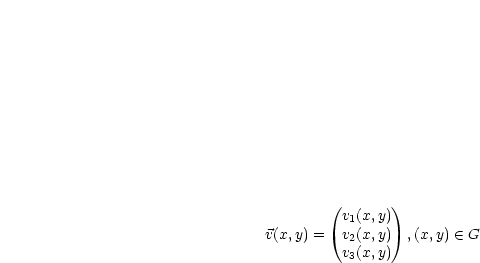
( ) v1(x,y) v(x,y) = v2(x,y) ,(x,y) (- G v3(x,y)

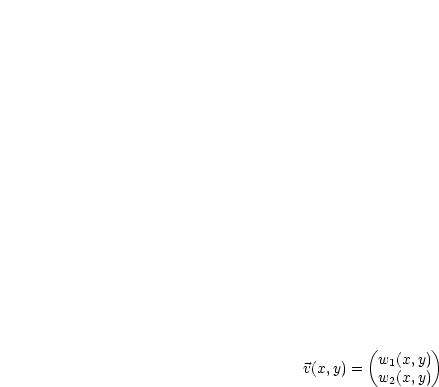
( ) v(x,y) = w1(x,y) w2(x,y)

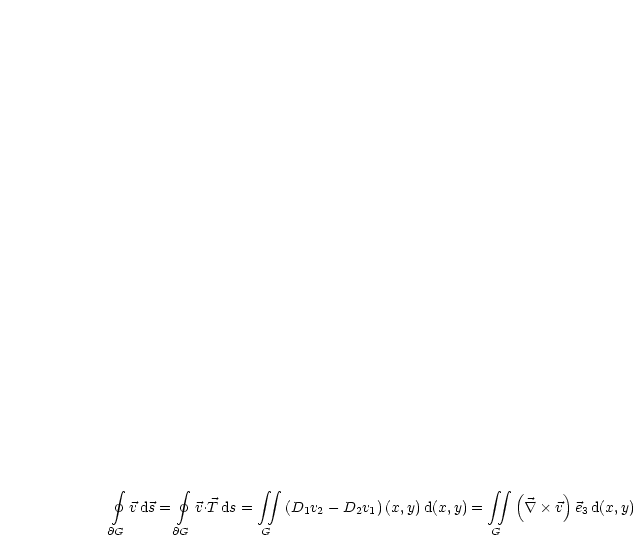
gf gf integral integral integral integral ( ) vds = v.T ds = (D1v2 - D2v1)(x,y)d(x,y) = \ ~/ × v e3d(x,y) @G @G G G

gf integral integral ( ) w .N ds = \~/ .w (x,y)d(x,y) @G G

4.4.3 GREENsche Formeln

Setze $w = \~/ f, f$ sei 2 mal stetig differenzierbar in $(D)$ :

$gf integral integral DN f ds = /_\ f d(x,y) @G G$

$f,g$ seien 2 mal stetig differenzierbare Skalarfelder: Setze in $(D) : w = g \~/ f$

$g \~/ f .N = gDN f$
$\~/ .(g \~/ f) = ( \~/ g) .( \~/ f) + g /_\ f$

1.GREENsche Formel:
$gf integral integral ( ) gDN f ds = \~/ g . \~/ f + g /_\ f d(x,y) @G G$
$( ) i ntegral integral [ ] D1gD1f + D2gD2f +g(D21f + D22f) d(x,y) G$
Vertausche $f$ und $g$ : $gf integral integral ( ) fDN g ds = \~/ f . \~/ f + f /_\ g d(x,y) @G G$
2.GREENsche Formel:
$gf integral integral ( ) ( ) gDN f - fDN g ds = g \~/ f -f \~/ g d(x,y) @G G$