|
|
|
|
|
|
|
Erinnerung: |
|
|
|
|
|
|
|
|
Erinnerung: |
|
|
Ist |
|
|
![[ ]
Jv(x) = D1v(x),D2v(x),...,Dnv(x) = (Djvk(x))
kij](ma3449x.gif)
Unser Ziel ist zu zeigen, daß  gilt. Bekannt ist
gilt. Bekannt ist  für
für  , 2,
, 2,  ,
,  .
.

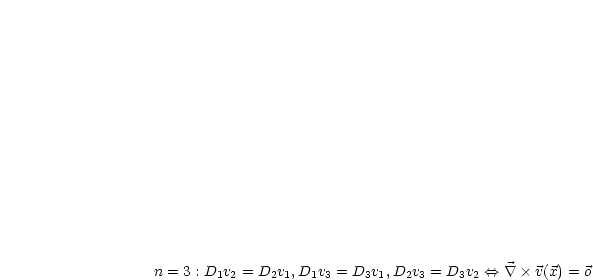
|
|
|
|
|
|
Es sei
|
Aus dem ersten Punkt folgt durch den zweiten Satz der zweite Punkt. Um (3) zu
beweisen gehen wir folgendermaßen vor: Das Ziel ist  , wobei
, wobei
 . Wir haben folgende Voraussetzung:
. Wir haben folgende Voraussetzung:
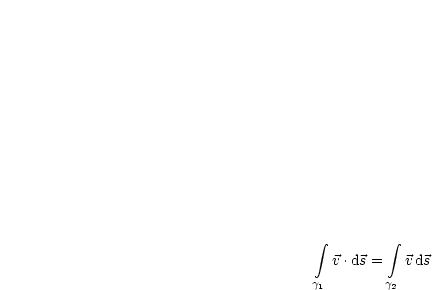

Nun zeigen wir noch die Umkehrung von (3) nach (2). Unser Ziel ist:

Bilde  und argumentiere wie vorher.
und argumentiere wie vorher.  beweisen wir dadurch,
indem wir zeigen, daß
beweisen wir dadurch,
indem wir zeigen, daß  ein Potentialfeld ist.
ein Potentialfeld ist.  sei beliebig, aber
fest:
sei beliebig, aber
fest:

Wir machen die Probe:  , wobei
, wobei  .
.

 sei eine gerade Verbindung zwischen
sei eine gerade Verbindung zwischen  und
und  mit
mit
 . Somit folgt nun (mit dem Mittelwertsatz der Integralrechnung):
. Somit folgt nun (mit dem Mittelwertsatz der Integralrechnung):

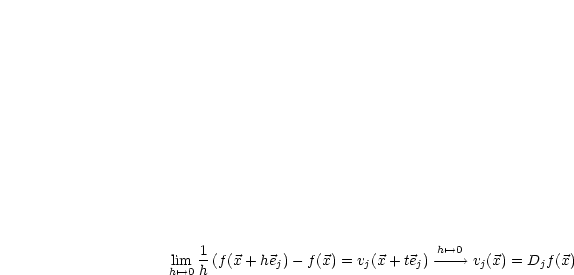
|
Das Gebiet |
|
|
Es sei |
|
Ist  nicht einfach zusammenhängend, so folgt im allgemeinen aus
nicht einfach zusammenhängend, so folgt im allgemeinen aus  nicht, daß
nicht, daß  Potentialfeld ist.
Potentialfeld ist.


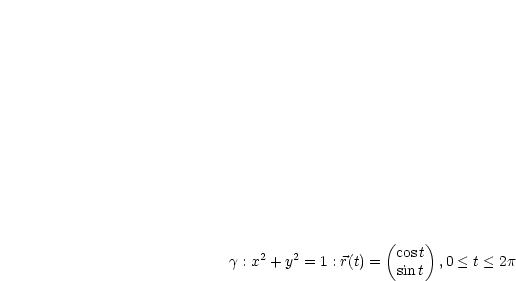
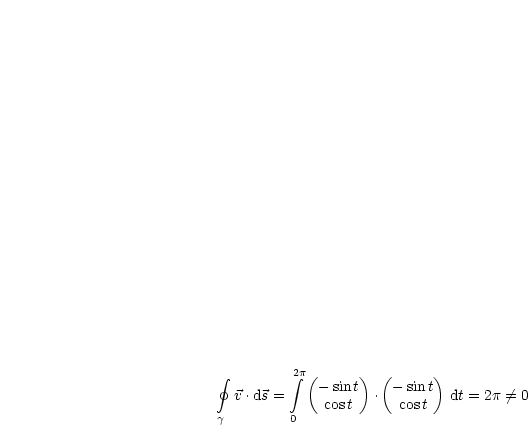
Somit folgt aus Satz 3, daß dies kein Potentialfeld ist.
Die Fläche  :
:  mit
mit  ,
,  :
:  ist einmal stetig
differenzierbar.
ist einmal stetig
differenzierbar.


![gf gf integral integral
v.ds = (v1 dx+ v2dy) = [D1v2(x,y) - D2v1(x,y)] d(x,y)
@G @G G](ma3519x.gif)



|
|
|
|
|



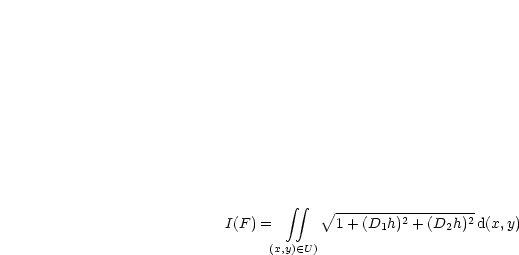
Obere Halbkugel  um (0,0,0) mit Radius
um (0,0,0) mit Radius  :
:
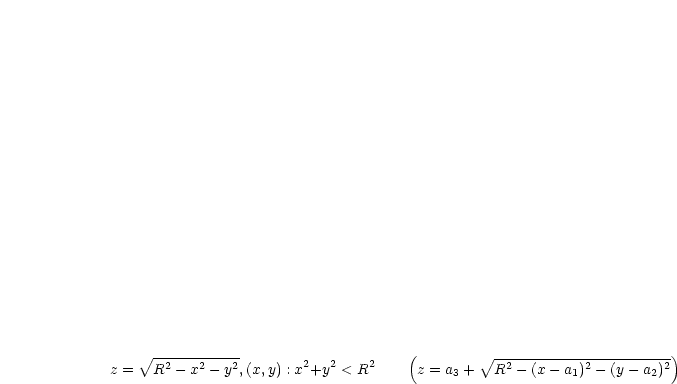
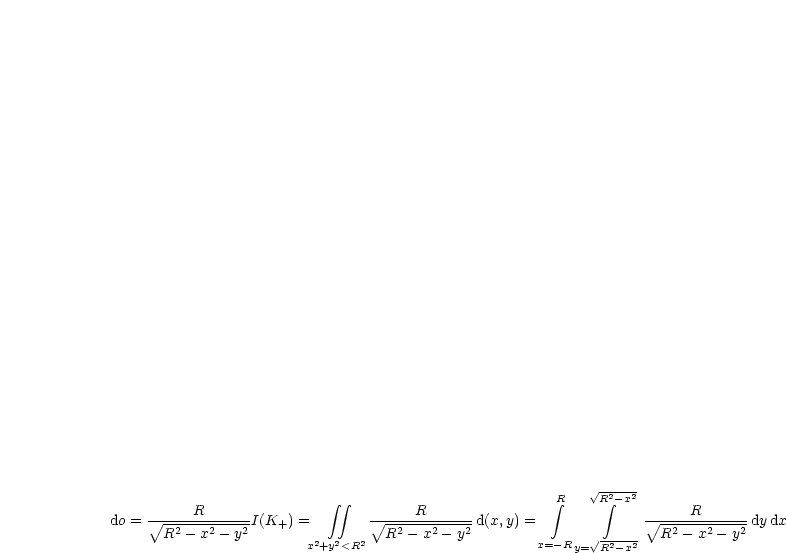
Wir verwenden Polarkoordinaten:



Nun wollen wir noch  mit Kugelkoordinaten berechnen:
mit Kugelkoordinaten berechnen:

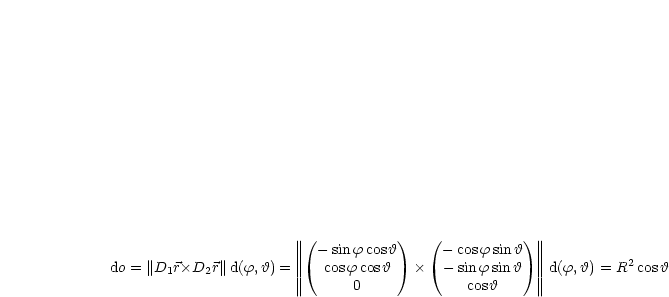
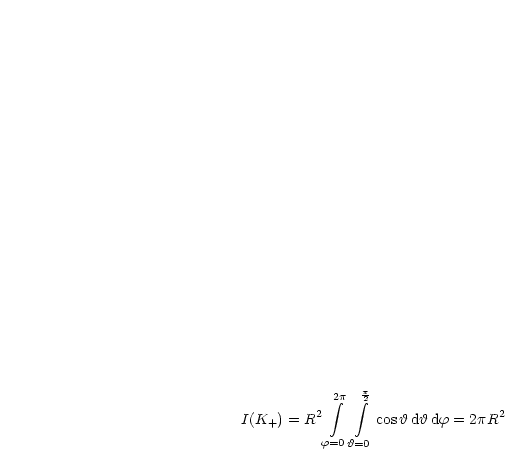
Wir wollen eine Rotationsfläche berechnen:




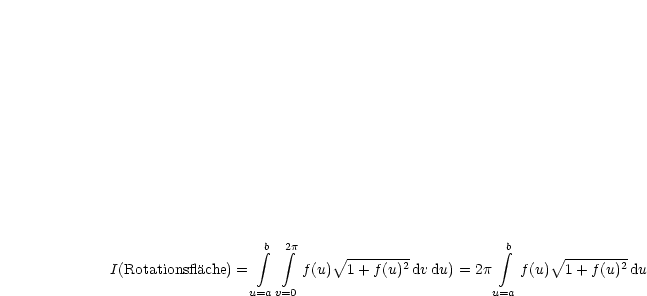
Kugeloberfläche!