[next] [prev] [prev-tail] [tail] [up]

4.6 Variable Substitution im Bereichsintegral

Definition:

Y sei eine Parametertransformation: Y(U *) = U,Y(G*),Y sei injektiv und stetig differenzierbar, detY(q,j) /= 0(> 0) .

( ) Y1 Y = Y2 , ( ) ( ) u Y1(q,j) v = Y2(q,j)

( ) ' D1Y1 D2Y1 Y (q,j) = D1Y2 D2Y2 , ' detY (q,j) = (D1Y1D2Y2 - D1Y2D2Y1) (q,j)

integral integral I(G) = d(u,v) G=Y(G*)

( ) ( ) @G*= r(t) = q(t) mit a < t < b, @G : R(t) = Y(q(t),j(t)) = Y1(r(t)) mit a < t < b j(t) -- -- Y1(r(t)) r(t)

integral integral gf integral b ' I(G) = d(u,v) = u dv = Y1(r(t))(Y2-o-r)-(t))dt G=Y(G*) @G a R'2(t)

(Y2 o r)'(t) = Y'2(r(t))r'(t)= \~/ Y2(r(t)).r'(t) -(1,2) (2,1)

integral integral integral b ( ) integral gf d(u,v) = Y1(r(t)) \~/ Y2(r(t)) .r'(t)dt= (Y1 \~/ Y2).ds = (Y1D1Y2 dq+Y1D2Y2 dj) G a ds|@G* @G* @G*

Nun wenden wir noch den GAUßschen Integralsatz an:

gf integral integral (Y1D1Y2- dq +Y1D2Y2- dj) = [D1(Y1D2Y2)-- D2(Y1D1Y2)] d(q,j) @G* v1 v2 G* detY'(q,j)

d(u,v) = |det(Y'(q,j)|d(q,j)

Satz:

Y,U,U *,G,G* sei wie vorher. f = f(u,v) sei stetig auf U . Dann gilt:

integral integral integral integral f(u,v)d(u,v) = f (Y(q,j))detY'(q,j)d(q,j) G=Y(G*) G*


In HM I hatten wir:
* integral integral ' Y : I '--> I : f(u)du = f(Y(q))Y (q)dq q u I=Y(I*) I*

Satz:

Es gelten die gleichen Voraussetzungen wie vorher auch. Dann erhält man:

integral integral integral integral integral integral I(F) = do = ||D r(q,j) ×D r(q,j)||d(q,j) = ||D r(u,v)× D r(u,v)||d(u,v) 1 2 1 2 F U* U------------ ------------- f(u,v)

integral integral integral integral f(u,v) d(u,v) = f(Y(q,j))detY'(q,j)d(q,j) * U U

Berechne mit der Kettenregel: D1r(q,j)× D2r(q,j) mit r.Y = r .

Beispiel:
( ) x3 3 v(x,y,z) = x2y ,(x,y,z) (- R x2z

Wir betrachten 2 2 F = {(x,y,z)| x + y = 1,0 < z < 1} : Hierdurch wird ein beschränktes Gebiet 3 G < R berandet. Gesucht ist der Fluß f von v durch F nach außen bezüglich G :

integral integral f = v.N do F

NF sei die Einheitsnormale nach außen, F1 die Seitenfläche und F2 , F3 die Deckflächen.

( ) cosu F1 : r(u,v) = sin u f¨ur 0 < u < 2p und 0 < v < 1 v

Wir rechen dies nach:

(cos u) N = D r(u,v)× D r(u,v)---------1----------= sin u 1 2 ||D1r(u,v)× D2r(u,v)|| 0

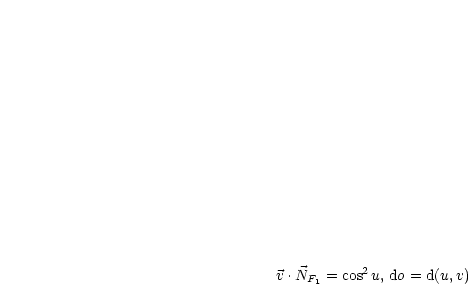
v.NF = cos2u, do = d(u,v) 1

integral v.N do = p F1

(r cosf) (1 ) F2 : r(r,f) = rsin f ,N = 0 1 0

integral p- v .N do = 4 F2

integral integral v .N do = 0 F3

4.6.1 Der STOKESsche Integralsatz in 3 R

Voraussetzung 1:

Voraussetzung 2:

Voraussetzung 3:

  1. @U sei positiv orientiert. Damit liegt T fest. Dann ist die Richtung von N die Richtung von D1r(u, v)× D2r(u,v) .
  2. v _L T in der Tangentialebene und ist nach außen bezüglich auf F gerichtet. N hat die Richtung von 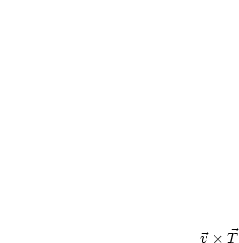v × T .

Wir wollen dies nun nachrechnen:

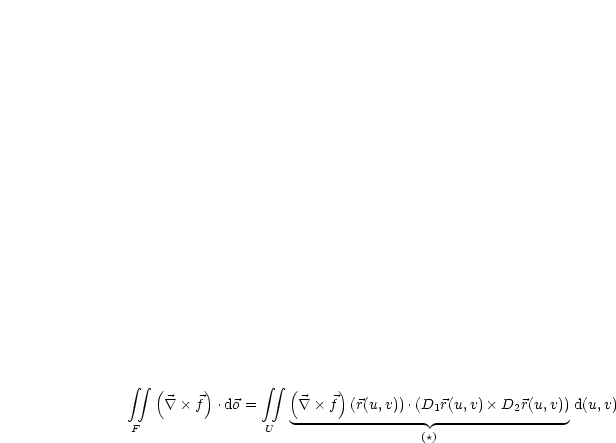
integral integral ( ) integral integral ( ) \ ~/ ×f .do = \~/ × f (r(u,v)).(D1r(u,v)× D2r(u,v))d(u,v) ---------------- ---------------- F U (*)

(*) geht nun durch Vertauschung der Faktoren des Skalarproduktes über in:

( ) (D1r(u,v)× D2r(u,v)). \~/ -×-f (r(u,v)) a× b c×d

[ ] ( ) ( ) (a×b).(c× d) = a.(b× (c×d)) = c (b.d)c- (b.c)d = b. (a .c)d - a. (b.c)d

Angewendet auf unsere Rechnung ergibt:

( ) ( ) D2r(u,v).(D1r(u,v). \~/ )f (r(u,v))-D1r(u,v). D2r(u,v). \~/ )f (r(u,v)) = (*)

(f .r)(u,v) = f(u,v) f

[ ] f'(u,v) = D1f(u,v),D2f(u, v) -- -- (3,2)

( ) ( ) D1f1 D2f1 D3f1 D1r(u,v). \~/ f1 D1f(u,v) = f'(r(u,v))D1r(u,v)= D1f2 D2f2 D3f2 (r(u,v)).D1r(u,v) = D1r(u,v). \~/ f2 = --- --- --- --- D1f3 D2f3 D3f3 D1r(u,v). \~/ f3 [( (3,3) (3,1)) ] = D1r(u,v) . \~/ f (r(u,v))
(4.3)

Nun folgt:

( ) ( ) D2r(u,v). (D1r(u,v). \~/ )f (r(u,v))- D1r(u,v). D2r(u,v). \~/ )f (r(u,v)) ---------- ---------- ---------- ---------- D1f(u,v) D2f(u,v)

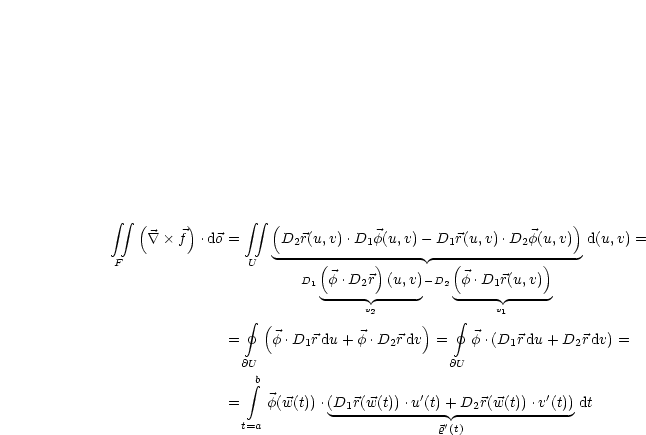integral integral ( ) integral integral ( ) \~/ × f .do = D2r(u,v).D1f(u,v) - D1r(u,v).D2f(u,v) d(u,v) = ------------------ ------------------ F U ( ) ( ) D1 f-.D2r-(u,v)-D2 -f.D1r(u,v)- v2 v1 gf ( ) gf = f .D1rdu + f.D2r dv = f .(D1r du+ D2r dv) = @U @U integral b = f(w(t)).(D1r(w(t)) .u'(t)+ D2r(w(t)).v'(t))dt t=a --------------'-------------- r(t)
(4.4)

Nun führen wir eine Zwischenrechnung durch:

( ' ) integral b gf r'(t) = r'(w(t))w'(t) = [D1r(w(t)),D2r(w(t))] u('t) = f(w(t))r'(t)dt = f.ds v(t) t=a @F

Beispiel:

f ,g seien skalare Felder:

3 3 2 f(x,y,z) = x - y + z

g(x,y,z) = x+ y+ z

F = {(x,y,z)|x2 + y2 + z2 = 1,z > 0}

Zu berechnen ist:

integral integral integral integral J := ( \~/ f × \~/ g).do = ( \~/ f × \~/ g).N do F F

N ist die Einheitsnormale auf F mit nichtnegativer z -Komponente.

1.Möglichkeit:
\~/ f × \~/ g = \~/ × v

( ) Wa¨hle v = f \~/ g : \~/ × f \~/ g = \~/ ×(f \~/ g)+\ ~/ × (f \~/ g) = ( \~/ f )×( \~/ g)+f ( \~/ -×-( \~/ g)) o

integral integral gf integral 2p (1) ( - sint) J = \~/ × (f \~/ g) .do = f \~/ g .ds = (x3- y3 + z2) 1 . cos t dt = 1 0 F2p @G 0 integral 3 3 [6 ]2p 3 = (cos t- sin t)(cost - sint)dt = 8 t = 2p 0 0
(4.5)

2.Möglichkeit:
{(x,y,z)|x2 + y2 < 1,z = 0}

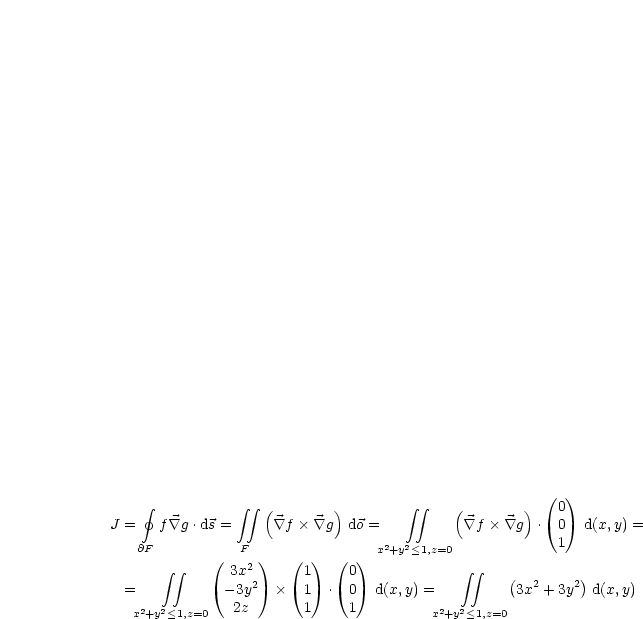( ) gf integral integral ( ) integral integral ( ) 0 J = f \~/ g .ds = \~/ f × \~/ g do = \~/ f × \~/ g . 0 d(x,y) = @F F x2+y2<1,z=0 1 integral integral ( 3x2) (1 ) (0 ) integral integral = - 3y2 × 1 . 0 d(x,y) = (3x2 + 3y2)d(x,y) 2z 1 1 x2+y2<1,z=0 x2+y2<1,z=0
(4.6)

Mit Polarkoordinaten erhält man:

x = rcost,y = rsin t

0 < r < 1,0 < t < 2p

integral 1 integral 2p 1 3 3 r2 .rdtdr = 3 .2p. 4 = 2 p r=0t=0

(siehe Induktionsgesetz, LENZsche Regel)

4.6.2 Substitution der Variablen im Volumenintegral

( ) x v : G (_ R3 '--> R3 : Y(u,v,w) = y z

v sei injektiv, stetig differenzierbar und es gelte detY(u,v,w) /= 0 mit (u,v,w) (- G .

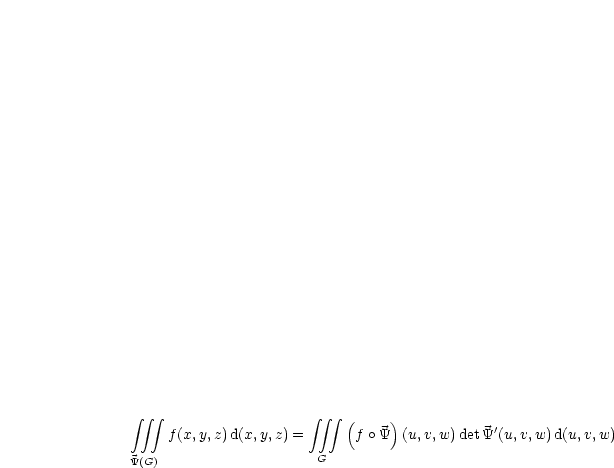
integral integral integral integral integral integral ( ) f(x,y,z)d(x,y,z) = f o Y (u,v,w)detY'(u,v,w)d(u,v,w) Y(G) G

Man kann dies auch anders schreiben, wenn man mehr Übung hat:

integral integral ( ) f(x)dx = f o Y (u)detY'(u)du Y(G) G

Beispiel:

Hier gibt es nun ein Beispiel zu Kugelkoordinaten u = r , v = f , w = h :

(x ) (r cosfcosh) Y(r,f,h) = y = rsin fcosh ,r > 0,0 < f < 2p,-p-< h < p- z rsinh 2 2

Man findet übrigens in vielen Büchern auch:

(r cosf sinh ) Y(r,f,h) = rsinf sinh rcosh

Es kommt in Anwendungen sehr häufig vor, daß man kugelsymmetrische Funktionen integrieren muß:

f = f(t),t (- R

g(x,y,z) = f(||x||),r2 > r1 > 0 -- -- x

( ) integral integral integral integral I = f(||x||)dx = f ( V~ x2-+-y2-+z2) d(x,y,z) V~ ------- r1<x<r2 r1< x2+y2+z2<r2

integral 2p integral r2 integral p2 integral r2 I = f(r)r2 cosh dhdr df = 2p .2. f(r)r2dr p f=0 r1 -2 r1

Als Funktion f(r) hat man nun beispielsweise:

r3 f (r) = e

integral 3 integral 1 r1 = 0,r2 = 1 : ex2+y2+z22 d(x,y,z) = 4p er3r2 dr = 4 p(e - 1) x2+y2+z2<1 0 r=r33

Zusammenfassung:

Zusammenfassend haben wir nun:

STOKESscher Satz: ( ) v1 integral integral ( ) gf G (_ R2 : v = v2 (- C1(G) : \~/ × v ezd(x,y) = v.ds v3 G @G

Integralsatz/GAUßscher Satz: ( w1 ) 1 integral integral gf w = w2 (- C (G) : \~/ .wd(x,y) = w .N ds G @G

STOKESscher Integralsatz: v : FR3 : integral integral ( ) gf \~/ × v .N do = v .T .ds F @F

GAUßscher Integralsatz im 3 R : integral integral integral integral integral \~/ .w dt = O@G w .Ndo G

[next] [prev] [prev-tail] [front] [up]