4.7 Der Gausche Integralsatz im <img src="msbm10-52.gif" alt="R" class="10x-x-52" />3

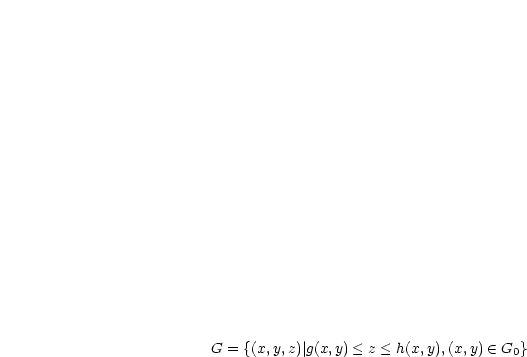
$R3 (_ G$ sei in $z$ -Richtung projizierbar: $G = {(x,y,z)|g(x,y) < z < h(x,y),(x,y) (- G0}$

( ) ( ) x D r× D r(x,y) - D1h(x,y) F1 : r(x,y) = y ,N do = ± --1-----2------||D1r× D2r|| d(x,y) = ± - D2h(x,y) d(x,y) h(x,y) ||D1r× D2r(x,y)|| 1

Das Minuszeichen benötigen wir nicht. Weiterhin folgt:

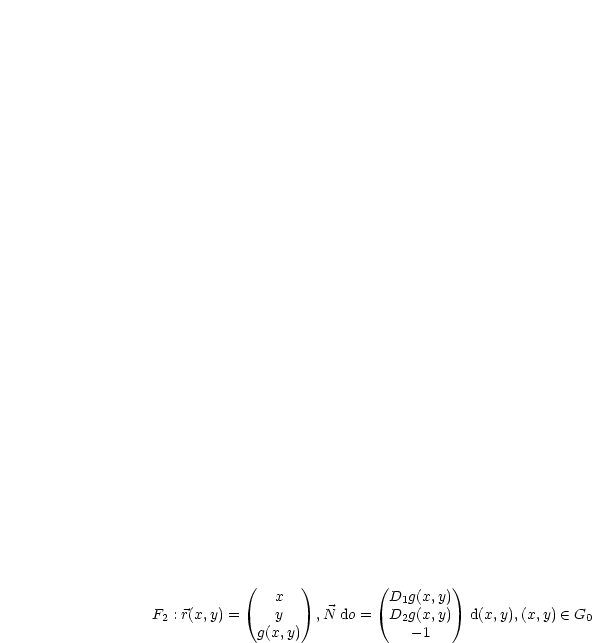
( ) ( ) x D1g(x,y) F2 : r(x,y) = y ,N do = D2g(x,y) d(x,y),(x,y) (- G0 g(x,y) - 1

( ) ... F3 : N do = ... do 0

Hier ist es zwar unwichtig, was in den ersten beiden Zeilen steht. Dennoch kann man es sich überlegen:

( ) ( ) x(s) x(s) @G0 : x = y(s) ,F3 : r(x,y,z) = y(s) -- -- z 0<x<L

g(x(s),y(s)) < z < h(x(s),y(s)),D r ×D r 1 2

$f : G '--> R$ sei stetig differenzierbar:

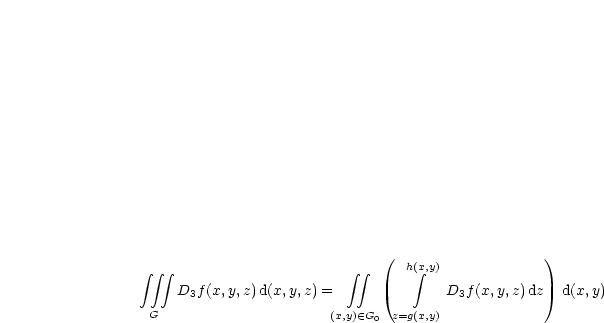
( ) integral integral integral integral integral h(x integral ,y) D3f (x,y,z)d(x,y,z) = D3f(x,y,z)dz d(x,y) G (x,y) (- G z=g(x,y) 0

integral integral integral integral integral D3f(x,y,z)d(x,y,z) = (f(x,y)h(x,y)- f(x,y)g(x,y)) d(x,y) = G (x,y) integral (- integral G0 integral integral = f(x,y,h(x,y))d(x,y)+ f(x,y,g(x,y))(- 1)d(x,y)+ (x,y) (- G integral 0 integral (x,y) (- G0 + f (F3) d(x,y) (x,y) (- G0

(4.7)