1.4 Besselsche Ungleichung/Parsevalsche Gleichung/Konvergenz im quadratischen Mittel

1.4 BESSELsche Ungleichung/PARSEVALsche Gleichung/Konvergenz im quadratischen Mittel

|z|2 = zz,|z- w|2 = |z| 2 +|w|2- 2Re (zw)

Oder:

|z|2 = zz,|z- w|2 = |z| 2 +|w|2- 2Re (wz)

Re(z) < |z|

2ab < a2 +b2 a,b (- R

$f$ sei wie in $(*)$ , $(ck)k$ seien komplexe Zahlen. Dann gilt mit den oben zusammengefaßten Bedingungen:

( ) || sum n ikx||2 2 sum n ikx sum n - -ilx sum n - -ikx |f (x)- cke | = |f (x)| + cke . cle - 2Re f (x)cke k= -n k=-n------ l=--n----- k=-n sum n - i(k-l)x ckcle k,l=-n

Nun führen wie eine Integration von $- p$ bis $+p$ durch:

( ) 1 + integral p|| sum n ||2 1 integral +p sum n - sum n- 2p- |f (x)- ckeikx| dx = 2p- |f(x)|2dx+ ckcldkl- 2Re ckf^(k) -p k= -n -p k,l=-n ---- k=-n sum n |ck| 2 k,l=-n

Somit gilt:

|----------------------------------------------------------------------| | integral +p| n | + integral p n ( n ) | |1-- ||f(x)- sum ceikx||2dx = -1- |f(x)| 2dx + sum |c|2- 2Re sum cf^(k) | |2p k=-n k 2p k= -n k k=-n k | ----p---------------------------p---------------------------------------

Es sei $^ ck = f(k)$ : $1 + integral p|| sum n ||2 1 integral +p sum n || ||2 2p- |f(x) - ^f(k)eikx| dx = 2p |f(x)| 2 dx- |^f(k)| - p k= -n -p k=-n$
Weiterhin gilt:
$sum n - sum n | || | sum n sum n | |2 2Re ck ^f(k) < 2 ||ck||||f^(k)||< |ck| 2 + ||f^(k)|| k=-n k=- n k=-n k= -n$
Wir multiplizieren mit $- 1$ und erhalten:
$|------ sum n----------- sum n------- sum n-|---|2| |-2Re ckf^(k) > - |ck| 2 - ||f^(k)|| | (**) | k=-n k=-n k=-n | -----------------------------------------|$
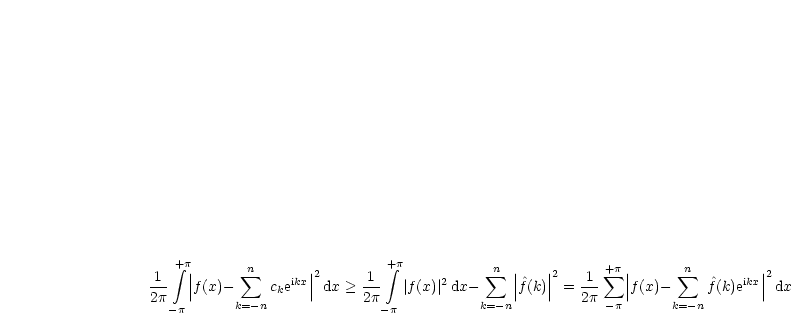
Aus (1) und $(**)$ folgt: $1 + integral p|| sum n ||2 1 + integral p sum n || ||2 1 sum +p|| sum n ||2 2p- |f(x)- ckeikx|dx > 2p- |f(x)| 2dx - |^f(k)| = 2p- |f(x)- f^(k)eikx| dx -p k=- n -p k=-n -p k=-n$

Satz:

Sei $f$ wie in $(*)$ . Dann gilt:

Der Ausdruck $1 integral +p|| sum n ||2 2p- |f(x)- ckeikx| dx -p k=-n$ wird genau für $ck = f^(k)$ minimal.

Satz (BESSELsche Ungleichung ):

Aus (2) folgt:

Für jedes $n (- N$ gilt: $sum n | | sum oo | | integral +p ||f^(k)||2 < ||^f(k)|| 2 < 1- |f(x)| 2 dx k=-n k=- oo 2p -p$ $^f(k) '--> 0$ für $k '--> oo$ .

Satz (PARSEVALsche Gleichung):

$f$ sei wie in $(*)$ . Es gilt:

$+p +p 1- integral || sum n ^ ikx||2 oo sum ||^ ||2 -1- integral 2 nli'-->mo o 2p |f(x)- f(k)e | dx = 0 <==> |f (k)| = 2p |f(x)|dx -p k=-n k=- oo -p$

Satz:

|--------------------------------| | integral +p| n | | | lim 1-- ||f(x)- sum ^f(k)eikx||2dx | |n'-->o o 2p k=-n | | -------p------ -------------- | | sum n ^f(k)eikx'-->f(x) f¨ur n'-->o o | | k=-n | --------im-quadratischen-Mittel=0-------

Beispiel:

Wir überprüfen den Satz:

{ 1 - p < x < a- p h(x) = 0 a - p < x < p

$a$ ist Zahl aus $(0,2p)$ . $f$ sei die $2p$ -periodische Fortsetzung von $h$ . Unser Ziel ist es nun, zu überprüfen, ob folgendes gilt:

+ integral p -1- 2 ? sum oo ||^ ||2 2p |f(x)| dx= |f(k)| -p k=- oo

Dazu berechnen wir zuerst das benötigte Integral:

+ integral p a integral -p -1- |f(x)| 2 dx =-1 dx = -a- 2p 2p 2p -p -p

Weiterhin gilt:

a- integral p | | 2 f^(k) = 1-- eikxdx, ^f(0) =-a-,|| ^f(0)|| 2 = a 2p 2p 4p -p

Für $k /= 0$ haben wir nun:

^ (-1)ki( -ika ) f(k) = 2pk e - 1

| |2 ---- ( )( ) |----------------| ||f^(k)|| = ^f(k).^f(k) =--122 eika- 1 e-ika - 1 = |--12-2 (1- coska)| 4p k -2p-k------------|

Nun folgt schlußendlich durch Einsetzen:

oo sum | |2 2 sum oo 2 oo sum sum oo ||f^(k)|| = -a2 + 1--co2s2ka-= -a-2 +-12- -12 - 12- cosk2a-= k=- oo 4p k=1 p k 4p p k=1k p k=1 k 2 2 ( 2 2) |---| + integral p = -a- + -1-p-- -1- (a---p)-- p-- = |-a-|= -1- |f(x)|2 dx 4p2 p2 6 p2 4 12 -2p- 2p -p

(1.2)

Hiermit wurde der Satz also überprüft. Man kann alternativ den Zusammenhang zwischen $ak$ , $bk$ und $f^(k)$ verwenden und in die PARSEVALsche Gleichung einsetzen:

2 sum oo ( ) + integral p |a0-| + 1 |ak |2 + |bk|2 = -1- |f(x)| 2 dx 4 2k=1 2p- p

[prev] [prev-tail] [front] [up]