4.1 Laurent-Reihe

[next] [tail] [up]

4.1 Laurent-Reihe

Wir wollen uns nun mit Reihen folgender Form beschäftigen:

+ oo sum m k=- oo k

Dieses erinnert stark an Fourierreihen:

sum oo sum N ckeikx = lim ckeikx k=- oo N'-->o o k=- N

Diese Reihen sind konvergent, falls _k=0_k und _k=1_-k konvergieren. Nun kommen wir zu den Laurent-Reihen. Eine Laurentreihe um z₀ ist von der Form:

sum oo k sum oo ( 1 )k oo sum k ak(z- z0) = a-k z--z0- + ak(z- z0) k=- oo k=1----- ------- k=0--- ----- Hauptteil Nebenteil

Satz 1:

|----------------------------------------------------------------------------------------|
| |
| k V~ ---- 1 sum oo k |
|Es seien r = lim sup |ak|, R =-------k V~ ----. Dann konvergiert die Laurent-Reihe akz f¨ur alle |
| lim sup |ak| k=- oo |
|z mit r < |z|< R. Beim Konvergenzbereich handelt es sich also um eine oo n Kreisring. Divergenz liegt
|vor f¨ur|z|< r oder |z| > R oder auch falls R < r. Gilt r < R, so stellt sum akzk in r < |z|< R eine
| k=- oo |
|holomorphe Funktion f dar. F¨ur r < r1 < r2 < R ist die Konvergenz auf dem Kreisring {z|r < |z|< r2}
|gleichma¨ßig. F¨ur jedes k (- Z und jedes r mit r < r < R gilt: |
| |
| -1- gf f(z) |
|ak = 2pi zk+1 dz |
| |z| =r |
-----------------------------------------------------------------------------------------

Begründung:

sum oo ( )k f1(z) = a-k --1--- k=1 z-- z0-- wk

Nun gilt für den Konvergenzradius für diese Reihe:

-----1 V~ ----= 1 lim sup k|ak| r

Für den Konvergenzbereich für den Hauptteil gilt:

1 1 z0 = 0 :|z--z-|< r :|z|> r 0

Der Nebenteil konvergiert für |z| < R. Für || = liegt gleichmäßige Konvergenz vor. Wir integrieren:

1 gf f(z) gf [ 1 oo sum ] sum oo 1 gf 2pi zk+1 = zk+1 anzn dz = an 2pi zn-k-1dz = ak |z| =r |z| =r n=- oo n=- oo |z| =r /=0 nur f¨ur n=k

Satz 2:

|-------------------------------------------------------------------------|
| |
|Es sei f im Kreisring {z| r < |z|< R}holomorph (r > 0, 0 < R < oo ). Dann gilt dort:
| |
| sum oo k |
|f(z) = ak(z- z0) |
| k=- oo |
| |
|F¨ur r < r < R gilt: |
| gf |
|ak =-1- --f-(z)k+1 dz f¨ur k (- Z |
| 2pi|z- z|=r (z - z0) |
| 0 |
|Die Laurententwicklung von f in r < |z- z0|< R ist eindeutig. |
| -------- |
--------------------------------------------------------------------------

Beweis:

Hier benötigen wir außerdem die geometrische Reihe:

sum oo qk = -1---f¨ur |q|< 1 k=0 1- q

Mit Satz 3 folgt nun:

gf gf gf -1- -f(z) -1- f(z)- -1- -f(z) f (z) = 2pi z - z dz = 2pi z- z dz + 2pi z - z dz = g gf |z|=R-d gf |z|=r+d = -1- 1f(z)-1---dz +-1- f(z)1--1-- dz = 2pi z 1- zz 2pi z1 - zz |z| =R -d |z|=r+d 1 gf 1 oo sum zk 1 gf 1 sum oo zk = 2pi zf(z) zk dz + 2pi f(z)z zk dz = |z| =R -d k= - oo |z| =r+d k=0 ( gf ) ( gf ) oo sum 1-- f-(z) k sum oo -1- k -k-1 = 2pi zk+1 dz z + 2pi f(z)z dz z k=0 ---|z| =R--d-------- k=0 |z| =r+d ak

(4.1)

Das erste Integral stellt die Koeffizienten a_k dar. Für den zweiten Ausdruck folgt durch Transformation der Summe:

( ) ( ) oo sum 1 gf k -k-1 - sum 1 1 gf f(z) l sum oo - k 2pi f(z)z dz z = 2pi zl+1 dz z = a- kz k=0 |z| =r+d l=- oo |z| =r+d k=1

Somit ergibt sich nun:

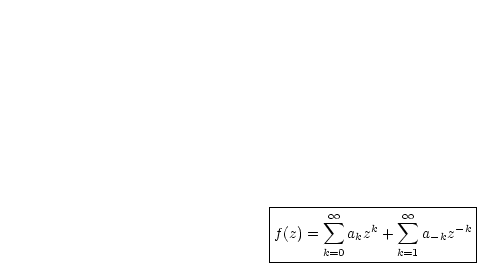
|-------------------------| | sum oo oo sum | f(z) = akzk + a-kz-k | ------k=0-------k=1--------

Definition:

$|----------------------------------------------------------------------------------------| | | |Ist f holomorph in {z||z- z0|< R}\{z0}aber in z0 nicht holomorph, so heiß t z0 isolierte Singularit¨at. -----------------------------------------------------------------------------------------$

\text{[math]}

z₀ sei eine isolierte Singularität. Berechne in 0 < |z - z₀| < R die Laurentreihe:

+ oo sum k --a-3--- --a--2-- -a--1-- 2 f(z) = ak(z-z0) = ...+ (z- z0)3 +(z- z0)2+ (z - z0)+a0+a1(z -z0)+a2(z-z0) +... k=- oo

Definition:

|----------------------------------------------------------------------------------------|
| |
|z0 heißt hebbare Singularit¨at, falls a- k = 0 fu¨r k = 1,2,...(Hauptteil=0), heißt Polstelle der Ordnung
|m (- N, falls ak = 0, k = m + 1,...und a- m /= 0. z0 heißt wesentliche Singularit¨at, falls ak /= 0 f¨ur
|unendliche viele k (- N. a-1 heißt Residuum-von f an der Stelle z0 und wir schreiben Res(f,z0).
-----------------------------------------------------------------------------------------

1z sum oo -1-1 e = k!zk ,| z|> 0 k=0

Für das sogenannte Residuum folgt nun mit k = -1:

gf Res(f;z ) =-1- f(z)dz fur 0 < r < R 0 2pi ¨ |z-z0| =r

Beispiel:

Folgende Funktion soll um 1 entwickelt werden, so daß Konvergenz in vorliegt. $1 f (z) = (z---1)(z---2)-$
1 und 2 sind isolierte Singularitäten:

Wir suchen somit die Laurentreihe, die im Bereich 0 < |z - 1| < 1 konvergiert. Damit folgt:
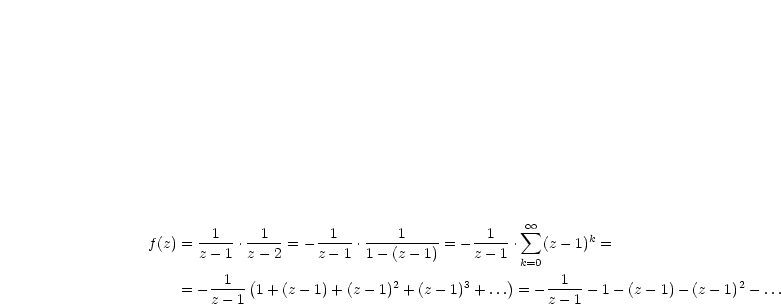$--1-- --1-- -1--- ----1----- --1-- o sum o k f(z) = z- 1 .z- 2 = - z- 1 .1- (z- 1) = -z - 1 . (z- 1) = ( ) k=0 = ---1-- 1+ (z- 1)+ (z -1)2 + (z- 1)3 + ... = --1-- 1 - (z - 1)- (z - 1)2 - ... z - 1 z- 1$ (4.2)

Somit folgt für das Residuum einfach durch Ablesen:
$Res(f;1) = - 1$
Nun soll die Funktion um 1, aber mit Konvergenz in , entwickelt werden. Der relevante Bereich ist somit |z - 1| > 1. Dann folgt:
$1 1 1 1 1 1 o sum o 1 f(z) = (z--1)(z---2) = z---1 .(z--1)---1 = (z--1)21---1 = (z--1)2 . (z---1)k = z-1 k=0 = ---1---+ ---1--- +... (z- 1)2 (z- 1)3$ (4.3)

Hier ist der Koeffizient a_-1 nicht vorhanden, woraus man aber nicht schließen darf, daß das Residuum 0 ist. Nur die erste Laurentreihe bei der isolierten Singularität liefert uns somit das Residuum.
Wir entwickeln um 0, wobei Konvergenz in vorliegen soll. Gesucht ist deshalb eine Reihe folgender Form: $-----1------ sum oo k f(z) = (z- 1)(z- 2) = akz mit|z|< 1 k=- oo$
Somit erhalten wir zwei geometrische Reihen, welche miteinander multipliziert werden:
$-----1------ --------1------- 1 oo sum k o sum o (z )j f(z) = (z- 1)(z - 2) = (1 -z) .2.(1- z)= 2 z . 2 ,| z|< 1 2 k=0 j=0$
Mittels des Cauchy-Produktes und der geometrischen Summe folgt als Ergebnis:
$|------ oo -(--------)---| f (z) = sum 1- -1-- zk | | k=0 2k+1 | ------------------------$
Eine andere Möglichkeit auf das Ergebnis zu kommen, wäre eine Partialbruchzerlegung.

Satz 3 (Taylorentwicklung):

|----------------------------------------------------------------------------------------|
|Ist f holomorph in D = {z||z - z0|< R}, dann gilt f¨ur z (- D: |
| |
| sum oo 1 gf f(z) 1 |
|f(z) = ak(z- z0)k mit ak = 2pi (z--z-)k+1 dz = k!f(k)(z0) f¨ur 0 < r < R. |
| k=0 |z-z0| =r 0 |
-----------------------------------------------------------------------------------------

Beweis:

Mittels des Satzes 2 folgt:

sum oo k f(z) = ak(z- z0) ,0 < |z- z0|< R k=- oo

1 gf a-k =--- f(z)(z- z0)k+1 dz f¨ur k = 1,2,... 2pi|z- z0|=r

Mit Hilfe des Cauchy-Riemannschen-Integralsatzes können wir sagen, daß hier das Ergebnis 0 ist:

-1- gf k+1 a- k = 2pi f(z)(z - z0) dz = 0 |z-z0| =r

Somit fallen die Koeffizienten a_-k weg, woraus dann folgt:

oo oo f(z) = sum a (z- z )k,0 < |z- z |< R = sum a (z - z )k,|z- z |< R k=- oo k 0 0 k=0 k 0 0

Folgerung 1:

Folgerung 2:

|----------------------------------------------------------------------------------------|
| |
|Ist f holomorph in |z- z0|< R, so gilt: |
| gf |
|f(z0) = -1- -f(z)-dz, 0 < r < R |
| 2pi|z-z | =r z- z0 |
|Dies ist die scho0n bekannte Cauchy-Integralformel. Diese Beziehung k¨onnen wir noch verallgemeinern:
| |
| (k) k! gf f(z) |
|f(z0) = 2pi (z--z-)k+1-dz, 0 < r < R, k = 0, 1, 2, ... |
| |z-z0| =r 0 |
-----------------------------------------------------------------------------------------

Beispiel:

gf ez 2pi pi z4 dz = 3!-f(3)(0) = 3- z0 = 0,r = 0,f(z) = ez.k = 3 |z|=1

[next] [front] [up]