4.2 Isolierte Singularitt und Residuensatz

4.2 Isolierte Singularität und Residuensatz

Wir fassen nochmals zusammen:

|----------------------------------------------------------------------------------------|
| |
|z0 sei isolierte Singularit¨at. Wir haben die Laurentreihe von oben. z0 heißt nun hebbar, falls ak = 0,
|k = -1,- 2,-3, .... z0 heiß t Polstelle der Ordnung m, falls a-k = 0, k = m + 1, m + 2, .... z0 heißt
|wesentliche-Singularit¨at, falls a-k /= 0 f¨ur unendlich viele k (- N. |
-----------------------------------------------------------------------------------------

Beispiel:

Hebbare Singularität: $f(z) = sinz- z$
z₀ = 0 ist eine isolierte Singularität. Wir berechnen die Laurentreihe:
$z- z3+ z5-± ... z2 z4 f (z) = ---3!-z-5!-----= 1- 3! + 5!± ...$
Es gilt nun f(0) = 1, womit gezeigt ist, daß z = 0 eine hebbare Singularität ist. Wir können dies auch folgendermaßen ausdrücken:
$lzim'-->z0f(z) bleibt beschr¨ankt.$
Polstelle: $f(z) =------1----- 0< |z-=1|<1 ---1--- 1 -(z - 1) ± ... (z -1)(z- 2) z - 1$
z₀ = 1 ist somit Polstelle 1.Ordnung.
$1 f(z) = (sin(z-))2 0$
z = 0 ist eine isolierte Singularität. Wir schreiben die Laurentreihe hin:
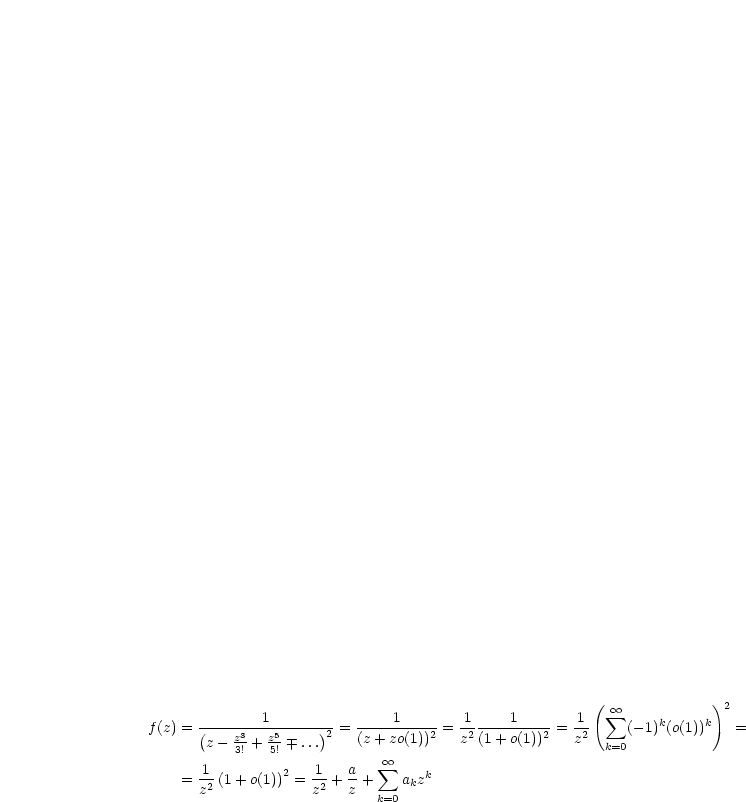$1 1 1 1 1 ( oo sum )2 f(z) = (----3---5-----)2 = ---------2 = -2--------2 = -2 (- 1)k(o(1))k = z- z3! + z5!± ... (z + zo(1)) z (1+ o(1)) z k=0 1 2 1 a sum oo = z2 (1+ o(1)) = z2 + z + akzk k=0$ (4.4)

Wir haben hier somit eine Polstelle 2.Ordnung.
Wesentliche Singularität: $1 sum oo -1-1 ez = k!zk k=0$
z = 0 ist eine wesentliche Singularität.

Nun ist noch eine Sache ungeklärt, und zwar, was nichtisolierte Singularitäten sind. Betrachten wir hierzu den komplexen Logarithmus:

log(z) = ln |z|+ iarg(z).-p < arg(z) < p

Jeder Punkt der negativen reellen Achse ist nichtisolierte Singularität.

f(z) = --1(-) sin 1z

z = 0 ist nichtisolierte Singularität. Für z_k = wird der Nenner 0. Ab einem gewissen k befinden sich alle Punkte innerhalb eines Kreises mit Radius . Diese Folge konvergiert, z = 0 ist Häufungspunkt dieser Folge, womit sie eine nichtisolierte Singularität darstellt.

Bemerkung:

f(z) sei bei einer wesentlichen Singularität nicht definiert. Betrachten wir f(z) = e. Es sei z = iy, womit für y0 kein Grenzwert existiert. Für z = x > 0 und x0 folgt |e^z|.

Satz 1:

|----------------------------------------------------------------------------------------|
| |
|f hat in z0 eine Polstelle der Ordnung m. Genau dann gibt es eine holomorphe Funktion g mit g(z0) /= 0
|und f(z) = --g(z)m-. Dann hat--1- Nullstellen m -terr Ordnung in z0. |
| (z- z0) f(z) |
-----------------------------------------------------------------------------------------

Beispiel:

1 1 f(z) = (z--1)(z--2) : f(z) = (z- 1)(z - 2)

Nun gilt:

f(z)(z- z0)m = am + am+1(z- z0)+ ...= g(z),g(z0) = am /= 0

Beispiel:

1 1 f(z) =--2--: f(z) = sin2 z sin z

Satz 2 (Residuensatz):

$|----------------------------------------------------------------------------------------| | | |G sei ein einfach zusammenha¨ngendes Gebiet. f : G \{z1,...zn}'--> C sei holomorph. z1, z2, ..., zn| |seien die isolierten Singularit¨aten von f. g sei eine geschlossene doppelpunktfreie Kurve in G mit zj / (- g |(j = 1, ..., n); g sei positiv orientiert. Dann gilt: | ||-------------(------------)-| | | gf s um | | || f(z) dz = 2pi Res(f;zj) , zj sei innerhalb von g, beispielsweise j = 2,3,4. | ||g j | | |------------------------------ | -----------------------------------------------------------------------------------------$

Beweis:

Mittels des zweiten Cauchy-Integralsatzes folgt:

gf gf f(z)dz = sum f(z)dz = sum 2pi .Res(f;zj) = 2pi. sum Res(f;zj) j j j g Kj

Beispiel:

z₀ sei Polstelle m-terr Ordnung. Dazu multiplizieren wir die Reihe mit (z - z₀)^m durch: $oo (z- z0)mf(z) = a-m +a -m+1(z- z0)+...+a- 1(z- z0)m -1+ sum ak(z -z0)k+m k=0$
Wir leiten diesen Ausdruck m - 1 mal nach z ab:
$|----------------------------------------------| |a = ---1---Dm -1[(z - z)mf (z)] = Res(f;z) | | -1 (m - 1)! 0 z=z0 0 | -----------------------------------------------$
Für m = 1 gilt beispielsweise:
$|--------------------------| -Res(f;z0)-=-(z--z0)f(z)| z=z0-|$
Hat f die Form f(z) = mit g(z₀)0, h(z₀) = 0, h'(z₀)0. Dann ist z₀ Polstelle 1.Ordnung. g und H seien außerdem holomorph. Dann folgt mit obiger Formel:
$(g ) g(z)|| Res h-;z0 = (z- z0)h(z)|| z=z0$
Da g und h holomorph sind, können wir diese in eine Reihe entwickeln:
$h(z) = h(z0)+(z -z0)h'(z0)+(z- z0)o(1) = (z-z0)h'(z0)+(z- z0)o(1)(z '--> z0)$
Durch Ausklammern von (z - z₀) folgt:
$h(z) = (z- z0)(h'(z0)+ o(1))$
Damit folgt nun durch Einsetzen:
$(h-- ) -------g(z)--------|| g(z0) Res g;z0 = (z- z0)(z - z0)(h'(z0) + o(1))|| = h'(z0) z=z0$
Wir wollen folgendes Integral berechnen: $gf e1z z--1-dz = 2pi(Res(f;0)+ Res(f;1)) |z| =2- - f(z)$
0 ist eine wesentliche Singularität und 1 eine Polstelle 1.Ordnung. Damit berechnen wir die Residuen an diesen beiden Stellen:
$| -e1z-|| Res(f;1) = (z - 1) z- 1|| = e z=1$
Da bei 0 eine wesentliche Singularität vorliegt, können wir obige Formel nicht anwenden. Wir müssen die Laurentreihe bilden:
$1 1 ( )( 1 1 1 1 1 ) -----ez = - 1+ z + z2 + ... 1+ - + ---2 +---3 + ... f¨ur|z|< 1 z - 1 z 2!z 3!z$
Wir multiplizieren die ersten Koeffizienten aus, wobei wir a_-1 erhalten:
$( )( 1 1 1 1 1 ) 1 ( 1 1 ) - 1 +z + z2 + ... 1+ - + ---2 + --3-+ ... = ...- - 1+ -- + --+ ... ... z 2!z 3!z z 2! 3!$
Mittels der Reihenentwicklung für die Exponentialfunktion folgt:
$oo sum 1 1 e = k! = 1 + 1+ 2! + ... k=0$

$1+ 1-+ 1-+ ...= e- 1 2! 3!$
Somit folgt für das Residuum:
$Res(f;0) = 1 - e$

[next] [prev] [prev-tail] [front] [up]