
In HM II hatten wir ein Linienintegral folgendermaßen berechnet:


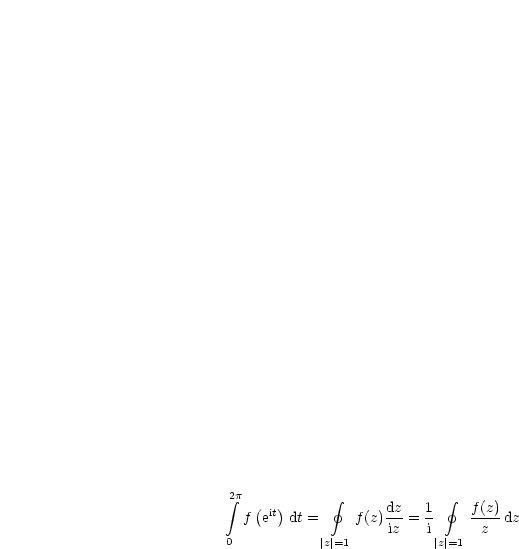
Dies ergibt dann den Residuensatz.


Dies stellt natürlich kein geschlossener Integrationsweg dar. Da wir aber eine periodische Funktion haben, folgt:
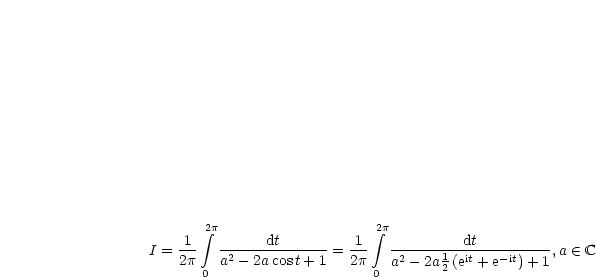
Außerdem gilt nun:

Durch Umformung von f(z) folgt:
Damit können wir nun das Integral berechnen:
a und ![]() sind Polstellen 1.Ordnung. Wir wenden den Residuensatz an:
sind Polstellen 1.Ordnung. Wir wenden den Residuensatz an:
Als Übung ist zu zeigen:
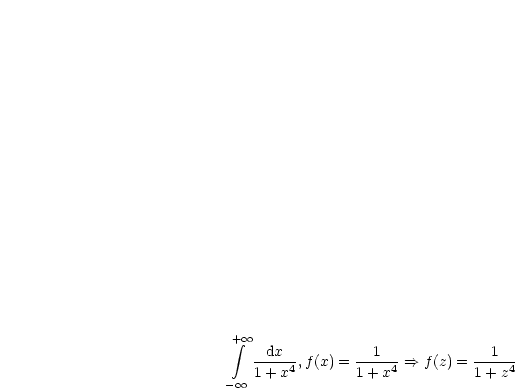
Die Singularitäten, also die Nullstellen des Nenners, sind folgende:
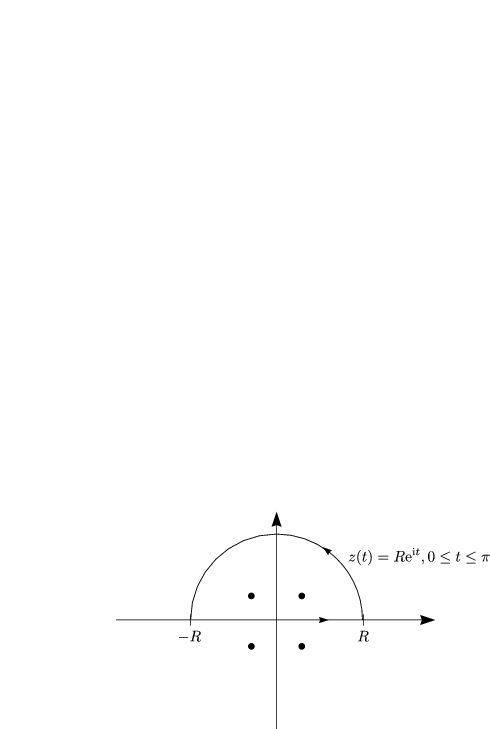

Wir hatten in HM I folgendes definiert:

Somit gilt:
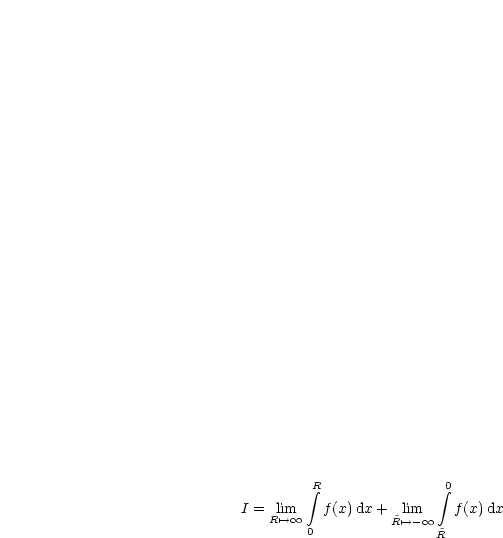
Ein kann sein, daß eine Integral nur als Cauchyscher Hauptwert, aber nicht als uneigentliches Integral existiert.


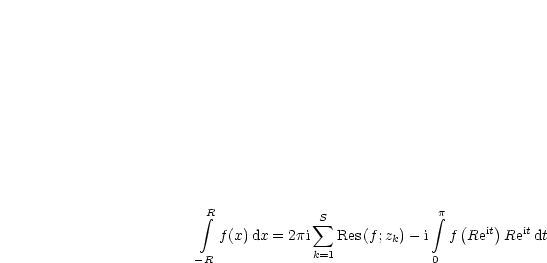
Wenn wir den Grenzübergang von R![]()
![]() bilden, folgt Satz 2.
bilden, folgt Satz 2.

Wir schätzen ab:

Damit folgt das Ergebnis:

Dies sind Polstellen 1.Ordnung. Damit folgt:
Das Ergebnis ist somit:
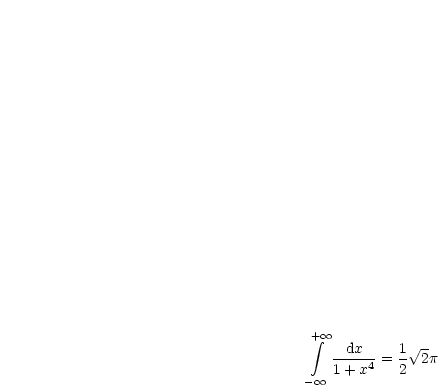

Wir berechnen das vorige Integral allgemein:

Da es sich um Polstellen erster Ordnung handelt, folgt:
Wir berechnen die Anzahl der Residuen im Intervall [0;![]() ]:
]:
Damit gilt:

Für das Integral folgt nun für gerades n:

Die Summe berechnen wir mittels der Formel für die geometrische Reihe:
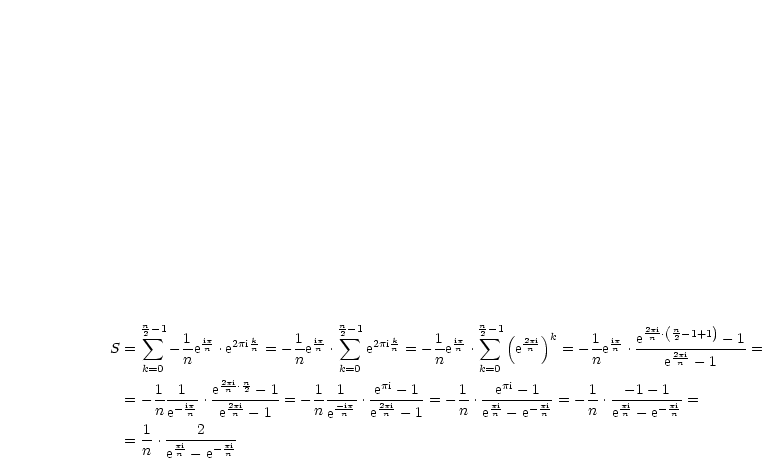 | (4.5) |
Damit folgt dann:
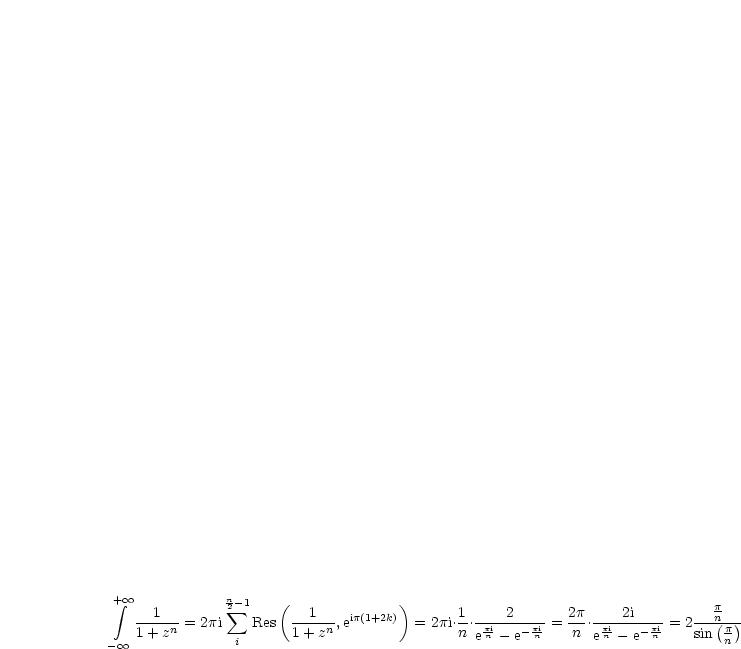
Setzen wir nun n = 4, so folgt:

Damit folgt also unser zuvor berechnetes Ergebnis.