5.6 Potenzreihenansatz

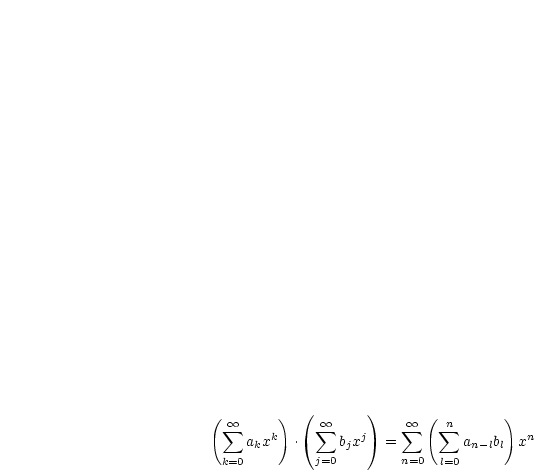
Wir wiederholen das Cauchy-Produkt aus HM I:

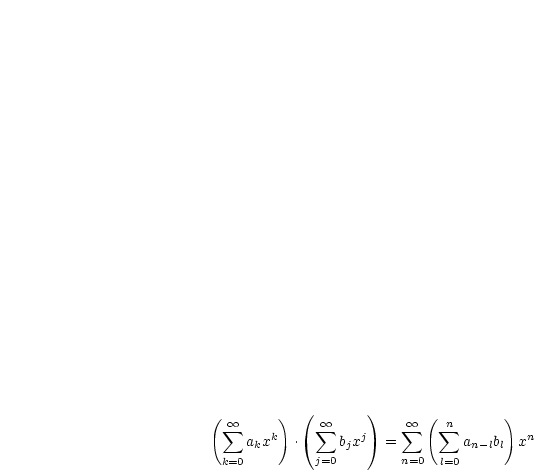
( oo ) ( oo ) oo ( n ) sum a xk . sum b xj = sum sum a b xn k=0 k j=0 j n=0 l=0 n-ll

Wir wollen uns nun mit folgender Differentialgleichung beschäftigen:

|----------------------| |Ly = y''+ p(x)y'+ q(x)y | -----------------------

Wir nehmen an, daß p(x) und q(x) Potenzreihen sind:

sum oo p(x) = pjxj j=0

oo q(x) = sum qkxk k=0

Die Reihen konvergieren innerhalb des gemeinsamen Konvergenzradius:

|x|< R

Wenn man sich beispielsweise mit der Schrödinger-Gleichung beschäftigt, erhält man folgende Differentialgleichungen:

Lagurerre-Differentialgleichung: $xy''(x)+ (1- x)y'(x) +ny(x) = 0$
Legendre-Differentialgleichung: $(1- x2)y''(x) -2xy'+ n(n + 1)y = 0$
Besselsche Differentialgleichung: $x2y''(x)+ xy'(x) +(x2 -n2)y = 0$
Hermitesche Differentialgleichung: $y''(x)- 2xy'(x) +2ny(x) = 0$

Sowohl die Legendre- als auch die Besselsche Differentialgleichungen treten insbesondere bei kugelsymmetrischen Problemen auf.

p(x) q(x) ~Ly = y''+ -x--y'+ -x2-y

oo oo p(x) = sum p xj,q(x) = sum qxk,|x|< R j=0 j k=0 k

Gesucht sind Lösungen bei x = 0, d.h. für x > 0 bzw. x < 0. x = 0 in der Gleichung oben heißt Stelle der Bestimmtheit oder reguläre singuläre Stelle.

Beispiel:

Wir betrachten die Eulersche Differentialgleichung:

2x2y''+3xy'- y = 0,0 < x < a

y''+ 31y'- -1- y = 0,p(x) = 3,q(x) = - 1 2x 3x2 2 2

Wir machen folgenden Ansatz:

y = xr,y'= rxr-1,y''= r(r - 1)xr-2

Durch Einsetzen geht die Differentialgleichung über in:

2r(r- 1)+ 3r -1 = 0

Durch Auflösen ergibt sich:

r1 = +1,r2 = -1 2

Damit folgt für die allgemeine Lösung:

|--------------------------------------------------| | 12 -1 | -y-=-C1x--+C2x---wobei-C1,C2-beliebige-Konstanten-sind-

Ein anderer Ansatz wird sein:

|----------- oo -----| |y(x,r) = xr sum ckxk| | k=0 | -------------------

Es handelt sich um einen verallgemeinerten Potenzreihenansatz (Methode von Frobenius).

Ly = x2y''+ xp(x)y'+q(x)y = 0

Hier wird als der Ansatz verwendet:

|------------------| | r sum oo k | |y(x,r) = x ckx | -----------k=0-----

2 '' ( 2 3 ) ' ( 2 ) Ly = x y + p0x + p1x + p2x + ... y + q0 + q1x+ q2x + ...y = 0

Regulärer Fall: $p0 = 0,q0 = q1 = 0$
Damit gilt:
$y''(x) + Potenzreihe .y'+ Potenzreihe .y = 0$
Singulärer Fall: $2 2 2 p0 + q0 + q1 /= 0$

oo sum sum oo y(x,r) = xr ckxk = ckxk+r k=0 k=0

' sum oo k+r-1 y = ck(k+ r)x k=0

sum oo y''= ck(k+ r)(k + r- 1)yk+r-2 k=0

Mit dem Cauchy-Produkt ergibt sich nun:

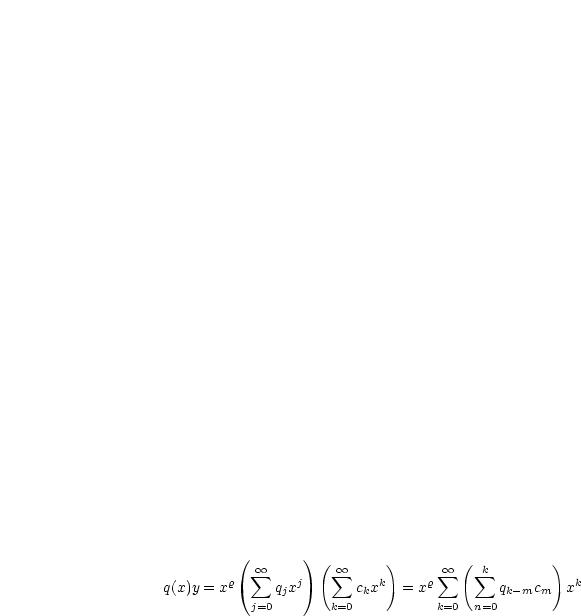
( oo ) ( oo ) oo ( k ) q(x)y = xr sum q xj sum cxk = xr sum sum q c xk j=0 j k=0 k k=0 n=0 k-m m

( oo ) ( oo ) oo ( k ) xp(x)y'= xr sum pjxj sum ck(k + r)xk = xr sum sum (m + r)pk-mcm xk j=0 k=0 k=0 m=0

oo sum x2y''= xr (k+ r)(k+ r -1)ckxk k=0

Diese Summen werden in die Differentialgleichung Ly = x²y'' + xp(x)y' + q(x)y eingesetzt:

oo sum [ sum k ] xr (k+ r)(k+ r- 1)ck + [(m + r)pk-mcm +qk-mcm] xk k=0 m=0

Sie Summanden zu k = 0 werden extra geschrieben:

[ [ ] ] r sum oo sum k k x r(r - 1) c0 + rp0c0 + q0c0 + (k+ r)(k + r- 1)ck + [(m + r)pk-mcm + qk-mcm] x k=1 m=0

[ sum oo ( xr c0(r(r- 1)+ rp0 + q0)+ ((k + r)(k + r- 1)+ (k+ r)p0 + q0)ck+ k=1 k sum -1 ) ] + [((m + r)pk-m + qk- m)cm] xk m=0

(5.2)

Wir führen folgende Abkürzungen ein:

f(r) = r(r - 1)+ p0r+ q0

Es handelt sich um das charakteristische Polynom für L. Das Ergebnis lautet mit y(x,) = x _k=0c_kx^k:

sum oo [ k sum -1 ] Ly = xrc0f(r)+ xr f (r + k)ck + [(m + r)pk-m + qk-m]cm xk k=1 m=0

Gesucht sind c₀, c₁, ... und derart, daß Ly = 0 ist für x > 0.

f()c₀ = 0
f( + k)c_k = - _m=0^k-1c_m mit k = 1, 2, ...

Es handelt sich hierbei um die Rekursionsformeln für c_k. Falls f( + k)0 für k = 1, 2, ..., dann kann man aus (2) alle c_k berechnen, falls c₀ bekannt ist:

0 c = - ---1--- sum [(m + r)p + q ]c = ----1--- (rp + q)c = c (r)c 1 f(r+ 1)m=0 1-m 1- m m f(r + 1) 1 1 0 1 0

1 sum 1 c2 = -------- [(m + r)p2-m + q2-m]cm = c2(r)c0 f(r+ 2) m=0

ck = ck(r)c0

_k() hängt ab von p₀, p₁, ..., p_k, q₀, q₁, ..., q_k, . Damit folgt im Ansatz:

y = xr(c0 + c1x+ c2x2 + c3x3 + ...)= c0xr(1+ c1x+ c2x2 + ...)

Es folgt zwingend, daß c₀0. Damit wählen wir c₀ = 1. Aus (1) folgt f() = 0 = ( - 1) + p₀ + q₀ = (² - ₁)( - ₂). Es handelt sich um eine quadratische Gleichung, die man unter anderem auch determinierende Gleichung nennt. Wir numerieren die so, daß ₁ > ₂. Für komplexe gilt Re > Re. Nun muß gelten:

f(r1 + k) = k(r1- r2 + k) /= 0 A k (- N

f(r + k) = k(k- (r - r )) /= 0, nur falls r - r (- /N 2 1 2 1 2

1.Ergebnis:
Setze = ₁, dann ist y₁(x) = x^₁c₀ mit c₀0 eine Lösung zu Ly = 0. $0 < x < R$

$- R < x < 0$
Weiteres Vorgehen:
- Regulärer Fall: $q0 = q1 = p0 = 0$
- Singulärer Fall: $r1- r2 / (- N$
  
  $r1- r2 (- N$
  
  $r1 = r2$
Es sind zwei linear unabhängige Lösungen gesucht.

[prev] [prev-tail] [front] [up]