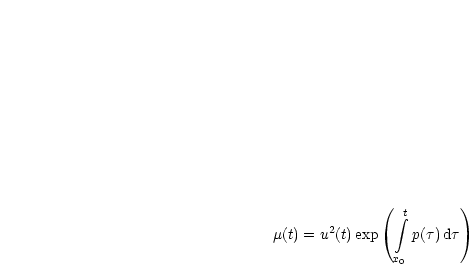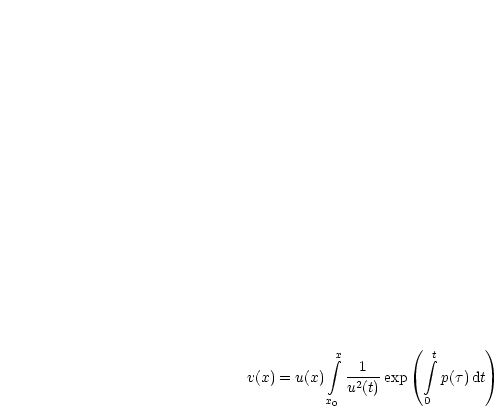[next] [prev] [prev-tail] [tail] [up]

5.5 Lösen des Problems A(f;a,b)

Wir wollen lösen:

Ly(x) = f(x),x (- I;y(x0) = a,y'(x0) = b

Vorbemerkung:

Es seien u, w (- C2(I).

'' ' ' L(u .w)(x) = w (x)u(x)+ w (x)(2u (x)+ p(x)u(x))+ w(x)Lu(x)

Hat man u (- LH mit u/=0, so gilt L(u,w)(x) = w''(x)u(x) + w'(2u'+ p(x)u(x)).

Satz 8:

|----------------------------------------------------------------------------------------| | | |Es sei u (- LHu /= 0. Dann gilt: | | ( ) | |Ist w allgemeine L¨osung von w''(x)+ w' 2 u'(x)+ p(x) = f(x) (1), so ist y(x) = u(x)w(x) die allge- | u(x) u(x) | |meine L¨osung von Ly = f. | -----------------------------------------------------------------------------------------

(1) ist lineare homogene Gleichung 1.Ordnung für w. Die Ordnung wurde also reduziert. Da Cu(x), c (- R ebenfalls (- LH ist, heißt dieses Vorgehen auch Variation der Konstanten.

( ) integral x( u'(t) ) u2(x) integral x u2(x) integral x m(x) = 2----+ p(t) dt = ln -2---+ p(t) dt =-2----exp p(t) dt x0 u(t) u (x0) x0 u (x0) x0

Wir multiplizieren Gleichung (1) mit m(x):

f(x) (w'(x)m(x))'= m(x)---- u(x)

Durch Integration von x0 bis x folgt:

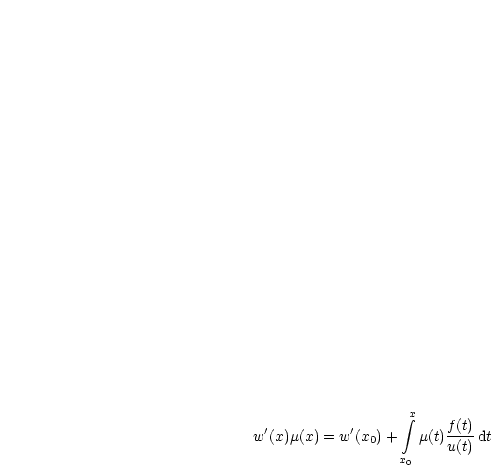
integral x w'(x)m(x) = w'(x0)+ m(t)f(t)dt x0 u(t)

x ' ' 1 integral f (t) w (x) = w (x0)m(x) + m(x) m(t)u(t) dt x0

integral x integral x integral x |_ integral s _| ds w(x) = w(x0)+ w'(x0) -dx- + |_ m(t)f(t)-dt _| -1--ds m(s) u(t) m(s) x0 x0 x0 x0

Damit folgt:

integral x x integral |_ integral s _| y(x) = u(x)+w(x) = w(x0)u(x)+w'(x0)u(x) -ds-+u(x) |_ f(t)m(t)-dt _| --1-ds m(s) u(t) m(s) x0 x0 x0

u(x), u(x) integral x0x-ds- m(s) sind linear unabhängige Lösungen der homogenen Gleichung:

( ) integral x ds u(x) u(x) ---- x0 m(s) det integral x dx 1 = u2(x)--1- /= 0 u'(x) u'(x) ---- +u(x)---- m(x) x0 m(s) m(x)

Suche die Linearkombination von u(x) und u(x) integral x0x-ds- m(s), die das Problem A(0,1,0) bzw. A(0,0,1), d.h. wie sind w(x0), w'(x0) zu wählen? Dann ist ayh1+byh2 Lösung von A(0;a,b).

Beispiele:
'' ' y - y cos(x) + ysin(x) = sin(x)

Die homogene Gleichung lautet:

y''- y'cos(x) + ysin(x) = 0

Gesucht ist eine Lösung u = u(x). Wir machen folgenden Ansatz:

u(x) = exp (v(x))

u'(x) = v'(x)exp(v(x))

u''(x) = (v'(x)2 + v''(x))exp(v(x))

Durch Einsetzen ergibt sich:

v''(x)+ v'(x)2 - v'(x)cos(x) +sin(x) = 0

v''(x)+ sin(x)+ v'(x) (v'(x)- cos(x)) = 0

(v'- cos(x))'+ v'(x)(v'(x)cos(x)) = 0

Wähle v' = cos(x) und v = sin(x).

|----------------| -u(x) =-exp(sin(x))-

Dies ist eine Lösung der homogenen Gleichung. Wir wählen nun einen anderen Ansatz. Wir suchen u (- LH in der Form ux) = v(sin(x)). Gesucht ist v = v(t) derart, daß u(x) = v sin(x) Lösung ist.

u'(x) = cos(x)v'(sin(x))

u''(x) = sin(x)v'(sin(x))+ cos2(x)v''(sin(x))

cos2(x)v''(sin(x))- sin(x)v'(sin(x))- cos2(x)v'(sin(x))+ v(sin(x))sin(x) = 0

( ) ( ) 1- sin2(x) v''(sin(x))- sin(x)v'(sin(x))- 1- sin2(x) v'(sin(x))+v(sin(x))sin(x) = 0

Wir sin(x) = t folgt:

(1 - t2)v''(t)- tv'(t) - (1 - t2)v'(t) +tv(t) = 0

(1- t2)(v''(t)- v'(t)) -t(v'(t)- v(t)) = 0

(1- t2)(v'(t) -v(t))'- t(v'(t)- v(t)) = 0

v'(t) = v(t) ==> v(t) = et

Somit gilt also:

|----------------| -u(x) =-exp(sin(x))-

Schauen wir uns die inhomogene Gleichung an:

y''- y'cos(x) + ysin(x)= sin(x) ------- ---'--- -(ycos(x))

(y'- y cos(x))'= sin(x)

Durch Integration folgt:

y'- y cos(x) = C - cos(x) 1

Wir multiplizieren mit dem integrierenden Faktor exp(- sin(x)).

(yexp (- sin(x)))'= C1exp(- sin(x))- cos(x)exp (- sin(x))

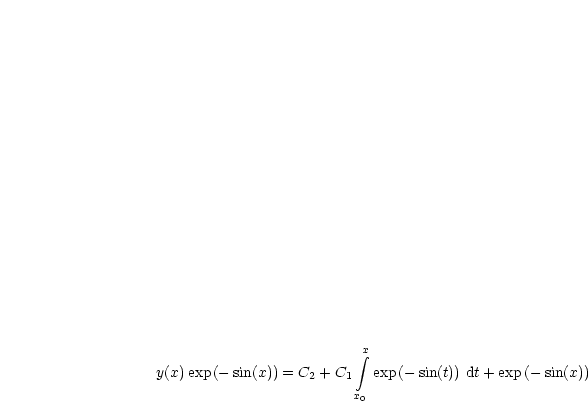
integral x y(x)exp (- sin(x)) = C2 + C1 exp (-sin(t)) dt+ exp (- sin(x)) x0

|---------------------------------x-------------------------------------| | integral | y(x) = C2exp(sin(x))+ C1 exp (sin(x)) exp(-sin(t)) dt + 1 C1,C2 beliebig | ---------------------------------x0-----------------yp-------------------

Beispiel:
'' ( 2) y (x)+ 1- x y(x) = 0

Ist y = y(x) Lösung, so ist auch u(x) = y(-x) Lösung. Dies soll als Übung gezeigt werden. Es gibt Lösungen, die gerade Funktionen sind und ungerade Funktionen sind. Wir machen folgenden Ansatz:

2 u(x) = v(x )

Als Übung wäre dann zu zeigen, daß sich durch diesen Ansatz folgende Differentialgleichung ergibt:

2t(2v'+ v)'+(1 -t)(2v'+ v) = 0

Ein anderer möglicher Ansatz ist:

u(x) = exp (v(x))

( ) u''(x) = v''(x)+ v'(x)2 exp(v(x))

v''(x)+ v'(x)2 + (1 - x2) = 0

Durch Anwendung der dritten binomischen Formel resultiert:

v''(x) = 1 + (v'- x)(v'+ x) = 0

' ' ' ' (v (x) + x)+ (v + x)(v - x) = 0

Wähle v'(x) = -x, wobei dann folgt:

1 2 v(x) = - 2x

Dann folgt die Lösung:

|---------(----)-| | x2 | |u(x) = exp - 2 | ------------------

Es gibt a1, a2 mit a12 + a22/=0 als Lösungen. Bilde hiermit die Funktion y = a1u + a2v. Da u, v (- LH, gilt auch y (- LH.

y(x ) = a u(x )+ a v(x ) = 0 0 1 0 2 0

y'(x0) = a1u'(x0)+ a2v'(x0) = 0

y (- A(0,0,0) ==> y(x) = 0 A x

Das heißt also:

a1u(x)+ a2v(x) = 0

u, v sind linear abhängig, was ein Widerspruch darstellt.

Satz 7:

|----------------------------------------------------------------------------------------| | | |u, v (- LH. W(u,v)(x0) /= 0 f¨ur ein x0 (- I. Dann gilt: | | | |W(u,v)(x) /= 0 A x (- I | -----------------------------------------------------------------------------------------

Wird das für f = 0 durchgeführt, so erhält man eine zweite von u linear unabhängige Lösung v der homogenen Gleichung:

integral x v(x) = u(x) -dt;m(t) = u2(t) x0 m(t)

( ) integral t m(t) = u2(t)exp p(t)dt x0

( ) integral x 1 integral t v(x) = u(x) u2(t) exp p(t)dt x0 0

[next] [prev] [prev-tail] [front] [up]