Wir betrachten die Differentialgleichung Ly(x) = y'' + p(x)y' + q(x)y = f(x) mit
x ![]() I und gegebenem p, q und f. Diese Funktionen seien außerdem stetig und
beschränkt.
I und gegebenem p, q und f. Diese Funktionen seien außerdem stetig und
beschränkt.
Es seien x0 ![]() I und
I und ![]() ,
, ![]()
![]()
![]() . Gesucht wird y
. Gesucht wird y ![]() C2(I) mit Ly(x) = f(x) und x
C2(I) mit Ly(x) = f(x) und x ![]() I
Außerdem sei y(x0) =
I
Außerdem sei y(x0) = ![]() und y'(x0) =
und y'(x0) = ![]() . Das Problem (P) wird mit A(f;
. Das Problem (P) wird mit A(f;![]() ,
,![]() )
bezeichnet. y
)
bezeichnet. y ![]() A(f;
A(f;![]() ,
,![]() ) soll bedeuten: y löst A(f;
) soll bedeuten: y löst A(f;![]() ,
,![]() ).
).

Es sei y ![]() A(0;0,0). Dann gilt:
A(0;0,0). Dann gilt:


Wir bezeichnen die Menge aller Lösungen als:
Diese Menge nennt man die „allgemeine Lösung“. Die „allgemeine Lösung der homogenen Gleichung“ lautet:

Dies bedeutet, daß y -yp = y0 eine Lösung der homogenen Gleichung ist.
Nun wollen wir die allgemeine Lösung der homogenen Gleichung LH charakterisieren. Mit Satz 1 ergibt sich:

Wir differenzieren:
Damit ist die Aussage gezeigt.

Alle Lösungen der homogenen Gleichung hat man, wenn man zwei linear unabhängige Lösungen hat, davon sind alle Linearkombinationen zu bilden; yh1 und yh2 leisten dies beispielsweise.
Jede Basis von LH heißt Fundamentalsystem von L. Beispielsweise bilden yh1 und yh2 ein Fundamentalsystem von L.
Es sei u, v ![]() C1(I). Dann nennt man folgende Matrix die Wronski-Matrix von u und
v:
C1(I). Dann nennt man folgende Matrix die Wronski-Matrix von u und
v:
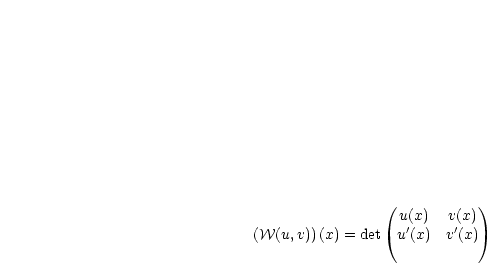

Dies schreiben wir in Matrixform:


Betrachten wir folgende Funktionen:
Die Funktionen sind linear unabhängig, wie sich an den Schaubildern erkennen läßt. Dies soll als Übung gezeigt werden durch:
u, v können nicht Lösungen einer homogenen linearen Differentialgleichung 2.Ordnung sein.
Es gibt ein x0 ![]() I mit W(u,v)(x0) = 0. Dann betrachten das Gleichungssystem für
I mit W(u,v)(x0) = 0. Dann betrachten das Gleichungssystem für
![]() 1,
1, ![]() 2:
2:

Aus W(u,v)(x0) = 0 folgt:
Es sei u, v ![]() LH. Dann folgt:
LH. Dann folgt:
Wir leiten eine Differentialgleichung für die Wronski-Determinante her:
|
| (5.1) |
Für die Lösung folgt:
