5.3 Der integrierende Faktor

Die Differentialgleichung f(x,y)dx + g(x,y)dy = 0 sei nicht exakt:

D2f (x,y) /= D1g(x,y)

Wir multiplizieren die Differentialgleichung mit einer beliebigen Funktion (x,y)0:

m(x,y)f(x,y)dx+ m(x,y)g(x,y)dy = 0 (2)

soll so bestimmt werden, daß die neue Differentialgleichung (2) jetzt exakt ist. Also muß gelten:

|----------------| |D2 (mf )=!D1 (mg) | -----------------

Falls dies gilt, heißt integrierender Faktor (Eulerscher Multiplikator). Oben muß nun die Produktregel angewendet werden, womit dann folgt:

(D2m(x,y))f(x,y)- (D1m(x, y))g(x,y) = m(x,y)(D1g(x,y)- D2f (x,y)) (3)

Dies ist eine partielle Differentialgleichung. Wir suchen einen Ansatz zur Berechnung von = (x,y). Es sei = (x,y) gegeben. Dann suchen wir eine Funktion H = H(t) derart, daß (x,y) = H((x,y)) ein integrierender Faktor ist. Mittels der Kettenregel ergibt sich dann wieder:

D1m(x,y) = H'(f(x,y))D1f(x,y)

D2m(x,y) = H'(f(x,y))D2f(x,y)

Gleichung (3) geht nun über in:

|----------------------------------------------| | ' D1g(x,y)- D2f(x,y) | |H (f(x,y)) = H(f(x,y)).D-f(x,y)-.f--D-f-.g(x,y)| -------------------------2------------1---------

Falls diese Funktion nur noch von (x,y) abhängt mit w((x,y)), dann hat der Ansatz etwas gebracht.

H'(f(x,y)) = H(f(x,y))w(f(x,y))

H'(t) = H(t)w(t)

Es ist eine lineare homogene Differentialgleichung. Diese Methode wollen wir nun an speziellen Beispielen üben:

(x,y) = x: (x,y) = H(x) $H'(x) = H(x) .D1g(x,y)--D2f-(x,y) - g(x,y)$
Falls dies nur von x abhängt, dann ist (x) = H(x) ein integrierender Faktor.
(x,y) = y $H'(y) = H(y) .D1g(x,y)--D2f(x,y) f(x,y)$
Dies darf nur von y abhängen.
(x,y) = x² + y² $' 2 2 2 2 D1g(x,y)--D2f-(x,y)- H (x + y ) = H(x + y ).2yf(x,y)- 2xg(x,y)$
Auch hier das die Funktion nur von x²+y² abhängen, damit (x) = H(x) integrierender Faktor ist.

Beispiel:

Schauen wir uns folgende lineare inhomogene Differentialgleichung an:

y'+ p(x)y +g(x) = 0

Daraus folgt:

(p(x)y + q(x))dx + 1 dy = 0 ---f(x,y)---- g(x,y)

Nun gilt:

D2f(x,y) = p(x)

D1g(x,y) = 0

Nun ergibt sich mit der obigen Beziehung:

D1g(x,y)--D2f(x,y)= -p(x)= p(x) - g -1

H'(x) = H(x)p(x)

Somit folgt:

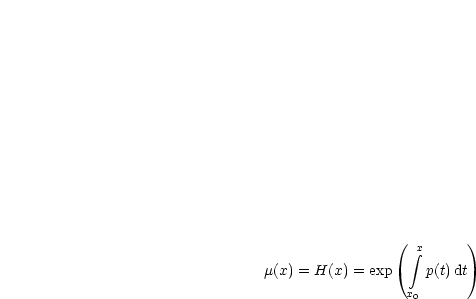
( ) integral x m(x) = H(x) = exp p(t)dt x0

Als Übung soll der Rest dieser Aufgabe gelöst werden.

Beispiel:

( 2 2 ) ' y- x + y + x y = 0

( 2 2 ) ydx - x + y + x dy = 0

D1g(x,y)- D2f(x,y) = - 2x- 1 -1 = -2 (x + 1)

Die Differentialgleichung ist somit nicht exakt. Die Fälle (1) und (2) liegen nicht vor.

2 2 f(x,y) = x + y

' -------2(x+-1)----- ----2(x+-1)---- ---1--- H (y) = H(y) .2y2 + 2x (x2 + y2 + x) = - 2(x2 + y2)(x + 1) = - x2 + y2

Wir haben somit nur eine Abhängigkeit von x² + y²; unser Ansatz führt infolgedessen zum Ziel. (x,y) = H(x² + y²) läßt sich aus H'(t) = H(t) berechnen.

H(t) = 1==> m(x,y) =---1--- t x2 + y2

Somit folgt also:

( ) --y---- --x---- x2 + y2 dx - 1 + x2 + y2 dy = 0

Nun müssen wir zu dem entsprechenden Vektorfeld ein Potential bestimmen.

--y---- D1h = x2 + y2

( ) ---x--- D2h = - 1+ x2 +y2

Nach einigen Rechenschritten folgt:

|--------------(--)----| |h(x,y) = arctan x- - y | ----------------y------|

Für die Lösung in impliziter Form folgt dann:

|------------------| | (x ) | |arctan -- - y = C | --------y----------

\text{[math]}

Schauen wir uns zum Abschluß noch einmal folgendes an:

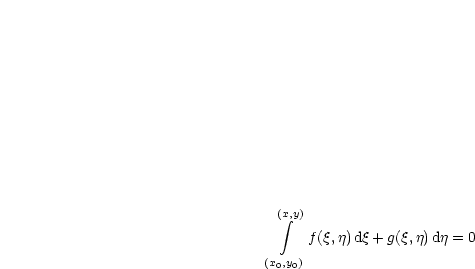
(x integral ,y) f(q,j)dq + g(q,j)dj = 0 (x0,y0)

Falls dieses Integral wegunabhängig ist, dann ist hierdurch die Lösung implizit gegeben.

<==> D f(q,j) = D g(q,j) 2 1

x integral integral y f(t,y0)dt+ g(x0,t) dt = 0 x0 y0

Die Exaktheit ist also eine andere Formulierung für die Wegunabhängigkeit eines Integrals. Als Vorbereitung zu unserem nächsten Thema wollen wir uns nochmals die inhomogene Differentialgleichung 1.Ordnung anschauen:

y'+ p(x)y = q(x)

Dies wird multipliziert mit:

( x ) integral m(x) = exp p(t)dt x0

Damit folgt dann:

' (my) (x) = m(x)q(x)

integral x m(x)y(x)- m(x0)y(x0) = m(t)q(t)dt x 0

Somit folgt:

|-----------------------------------| | integral x | y(x) = y(x0) + -1-- m(t)g(t)dt | | m(x) m(x)x | | L¨osung der ----0- ------ | | hoGmleoicghenuenng GLle¨oisuchnugn dge yr inmhiotm yo(gxene)n=0 ------------------------p----p-0-----

Es handelt sich um alle Lösungen, falls x₀ beliebig ist. Für g(x) = 0 folgt daraus auch die Lösung der homogenen Gleichung:

y(x0) C y(x) = m(x)-= m(x) mit beliebigem C

[next] [prev] [prev-tail] [front] [up]