5.2 Exakte Differentialgleichungen und integrierender Faktor

[next] [prev] [prev-tail] [tail] [up]

5.2 Exakte Differentialgleichungen und integrierender Faktor

y'= f(x,y) = - f(x,y) g(x,y)

Wir multiplizieren mit g(x,y)0 und bringen alles auf eine Seite:

' f (x,y)+ g(x,y)y = 0

Wir suchen eine Lösung in Parameterdarstellung x = x(t), y = y(t). Wir setzen dies ein und erhalten:

˙y(t) f (x(t),y(t))+ g(x(t),y(t)).˙x(t)-= 0

f(x(t),y(t))x˙(t)+ g(x(t),y(t))˙y(t) = 0 (*)

˙y(t) = dy, ˙x(t) = dx dt dt

Wir multiplizieren mit dt durch:

f(x,y)dx+ g(x,y)dy = 0 (1)

In dieser Differentialgleichung ist die explizite Form y = y(x) enthalten, die implizite Form x = x(y) und außerdem die Parameterdarstellung x = x(t), y = y(t). Lösen von (1) bedeutet:
Suche x = x(t), y = y(t) ¹(J) (J ²) mit (*). Die Voraussetzung ist nun, daß f, f C¹(G), wobei G ein einfach zusammenhängendes Gebiet in ² ist.

f2(x,y)+ g2(x,y) /= 0 mit (x,y) (- G

Ordne (1) folgendes Vektorfeld zu:

( ) f(x,y) v(x,y) = g(x,y)

(*) kann dann so geschrieben werden mit (t) = :

v(r(t)).˙r(t) = 0

p(t) = \~/ h(r(t)).r˙(t)

Ist ein Potentialfeld, d.h. = $\~/$ h, dann ist h((t)) = const.

Definition:

|----------------------------------------------------------------------------------------|
| |
|Die Gleichung (1) heißt exakt in G, falls v in G ein Potentialfeld ist, d.h. |
| |
|D2f(x,y) = D1g(x,y) f¨ur (x,y) (- G |
-----------------------------------------------------------------------------------------

Satz 1:

|----------------------------------------------------------------------------------------|
|Es sei die Differentialgleichung (1) in G exakt und h ein Potentialfeld zu v. Dann sind alle L¨osungen von
|(1) implizit und h(x,y) = C (beliebig) gegeben. (Jede H¨ohenlinie von H ist L¨osung von (1) und jede
|L¨osung von (1) ist H¨ohenlinie von h.) |
| |
-----------------------------------------------------------------------------------------

Beweis:

Wir notieren uns nochmals Gleichung (1):

f(x,y)dx+ g(x,y)dy = 0

D2f (x,y) = D1f(x,y)

h(x,y) = C definiert implizit die Kurve (t) = mit h(x(t),y(t)) = C.
Wir differenzieren dies nach t: $0 = \~/ h(x(t),y(t)).˙r(t) A t (- J ----- ----- v(r(t))$
((t)) ^.(t) = 0 $Dth(r(t)) ==> h(r(t)) = const.$

Beispiel:

Wir betrachten die Differentialgleichung:

y'= p(x)q(y)

p(x)q(y)dx - dy = 0

Diese Gleichung ist auf keinen Fall exakt. Deshalb dividieren wir durch q(y) durch:

1 p(x) dx- q(y)dy = 0

Diese Differentialgleichung ist nun exakt. Also können wir die neue Methode anwenden:

p(x) = D1h

q(y) = D2h

Es gilt also:

D1h(x,y) = p(x)

Daraus resultiert:

integral x h(x,y) = p(t)dt+ c(y) x0

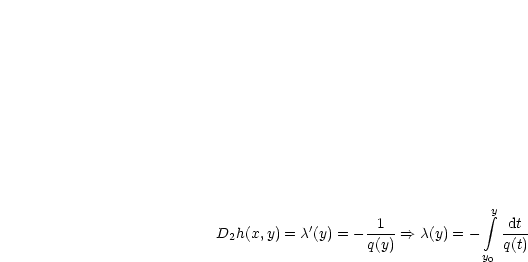
1 integral y dt D2h(x,y) = c'(y) = -----==> c(y) = - ---- q(y) y0 q(t)

Also folgt:

|----------------------------| | integral x integral y dt | |h(x,y) = p(t)dt- ----= C | | x0 y0 q(t) | -----------------------------

Dies sind alle Lösungen für x₀, y₀ und beliebigem C. Die Lösung durch (x₀,y₀) erhält man für C = 0.

[next] [prev] [prev-tail] [front] [up]