3.1 Einleitung

In diesem Abschnitt werden wir zwei wichtige Sätze kennenlernen:

In HMII hatten wir ein Linienintegral folgendermaßen definiert:

integral integral b vds = v(r(t)).˙r(t)dt mit g : r = r(t),a < t < b und ds = ˙r(t)dt g a

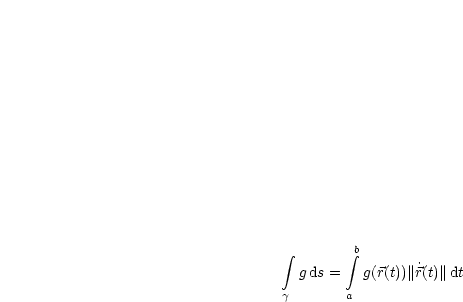
integral integral b g ds = g(r(t))||˙r(t)||dt g a

Integration über den Viertelkreis im 1.Quadranten der komplexen Ebene: $f (z) = z2$
Wir benötigen eine Parameterdarstellung für den Kreis:
$z(t) = eit,0 < t < p 2$
Wir setzen diese Darstellung in die Funktion f(z) ein:
$f(z(t)) = e- 2it$

$it z˙(t) = ie$
Daraus folgt nun das Integral:
$p integral - integral 2 [ ]p z2dz = i e-i2zeitdt = -e -it20 = 1+ i g 0$
l-facher Kreisdurchlauf: $f(z) =---1--k,k (- Z (z- a)$

$a : C$
g : |z - a| = r soll l mal im positiven Sinn durchlaufen werden:
$it z(t) = re + a,0 < t < l.2p$

$it ˙z(t) = i.re = i(z(t) - a)$
Somit folgt durch Einsetzen in die Funktion f(z) wiederum:
$f(z(t)) =----1---k = r-ke-ikt (z(t) - a)$
Das Integral ergibt sich nun folgendermaßen:
$i2pl f¨ur k = 1 integral dz integral 2pl integral 2pl { (z---a)k-= r-ke-ikt .ireitdt = irik e(1-k)tdt = 0 f¨ur k /= 1 g 0 0$

$\text{[math]}$
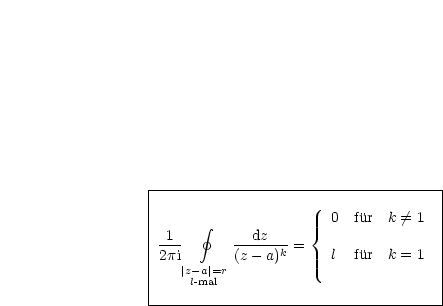
Das Ergebnis hängt nicht von r ab.
Kompliziertes Integral: $gf z |z| e2 dz |z| =z z$

$z(t) = zeit,0 < t < 2$
Nun folgt mit dem Beispiel vorher.
$gf ( 2 3 ) gf ( 2 ) z 1- 1+ z + z-+ z- + ... dz = 2 -1 + 1+ 1-+ z-+ z- + ... dz = 4pi |z| =z z2 2! 3! |z| =z z2 z 2! 3! 4!$