3.2 Stze ber komplexe Kurvenintegrale

[prev] [prev-tail] [tail] [up]

3.2 Sätze über komplexe Kurvenintegrale

Satz 1 (Integralsatz von Cauchy):

|----------------------------------------------------------------------------------------|
| |
|Es sei f holomorph im einfach zusammenha¨ngenden Gebiet G < C. Dann gilt f¨ur jede st¨uckweise glatte
|geschlossene Kurve g < G: |
| gf |
| |
| f(z)dz = 0 |
|g |
-----------------------------------------------------------------------------------------

\text{[math]}

Begründung:

gf f(z)dz g

Wir zerlegen die Funktion f(z) in Real- und Imaginärteil:

f(x+ iy) = u(x,y)+ iv(x,y)

Des weiteren gilt durch Parametrisierung:

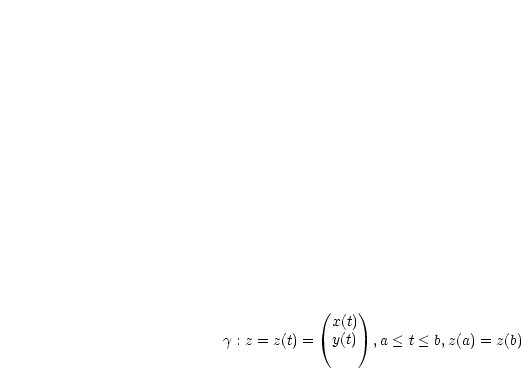
( ) x(t) g : z = z(t) = y(t) ,a < t < b,z(a) = z(b)

( u ) (x˙) (v) ( ˙x) f(z(t))˙z(t) = u(x(t),y(t))+iv(x(t),y(t))(˙x(t) +i˙y(t)) = - v . y˙ +i u . y˙

Somit folgt durch Einsetzen in das Integral:

gf integral b( u ) (x˙) integral b(v ) (x˙) f(z)dz = - v . y˙ dt+ i u . y˙ dt g t=a a

Da sowohl als auch Potentialfelder sind (siehe HMII), so folgt:

gf f(z) dz = 0+ 0 = 0 g

Bemerkung:

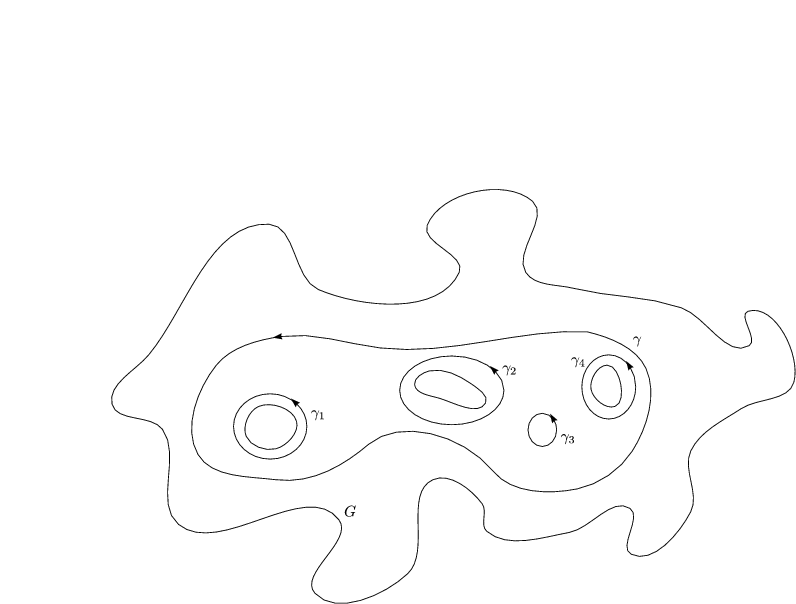
Setzt sich eine Kurve aus mehreren Teilkurven _i zusammen, so ergibt sich das Integral über als Summe der einzelnen Integrale über _i:

integral sum integral f(z)dz = f(z)dz g i=1gi

Die Integration hängt natürlich auch von der Orientierung der Kurve ab. Die obige Formel gilt nur, wenn die Teilkurven _i dieselbe Orientierung haben. Besitzt die Parametrisierung z = z(t), a < t < b, so gilt für die Kurve ^- mit entgegengesetzter Orientierung beispielsweise die Parametrisierung:

g- : z = z(b+ a - t),a < t < b

Beispiel:

f(z) = z,G =

sei geschlossene Kurve:

z = z(t),a < t < b,z(a) = z(b)

gf integral b integral b ( ) ( ) zdz = z(t)˙z(t)dz = 1 z2(t)'dt = 1 z2(b)- z2(a) = 0 g t=a 2t=a 2

Dies gilt unabhängig von der Kurve .

Satz 2 (Folgerung aus Satz 1):

|----------------------------------------------------------------------------------------|
| |
|G < C sei Gebiet und f : G '--> C sei holomorph. g, g1, g2, ..., gm seinen st¨uckweise glatte, geschlossene,
|doppelpunktfreie, im selben Sinn orientierte Kurven. g1, ..., gm verlaufen im Innengebiet von g und gj
|verl¨auft im Au ßengebiet von gk (k /= j). Das Gebiet zwischen g und g1, ..., gm liegt im Gebiet G. Dann|
|gilt: |
| |
| gf sum m gf |
| f(z)dz = f(z)dz |
|g k=1gk |
-----------------------------------------------------------------------------------------

Beispiel:

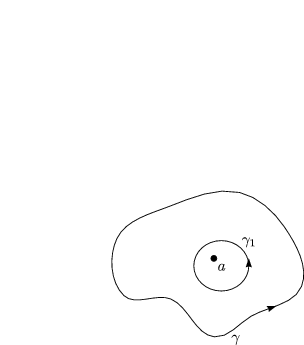
Wir betrachten folgendes Fundamentalbeispiel:

gf ---1---dz g (z- a)k

sei doppelpunktfreie, geschlossene Kurve um a. k seinen ganze Zahlen: k .

G = C \{z = -a}

m = 1,g1 :| z - a|= r

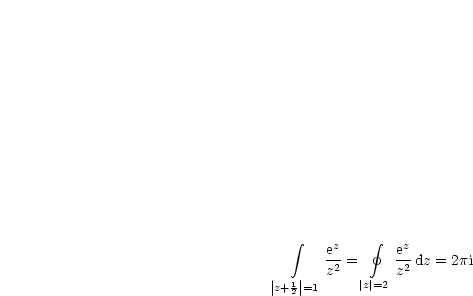
Daraus folgt nun:

gf dz { 2pi f¨ur k = 1 ------k = |z-a|=r (z -a) 0 f¨ur k /= 1

Beispiel:

integral gf ez= ez-dz = 2pi z2 z2 |z+12|=1 |z|=2

Beispiel:

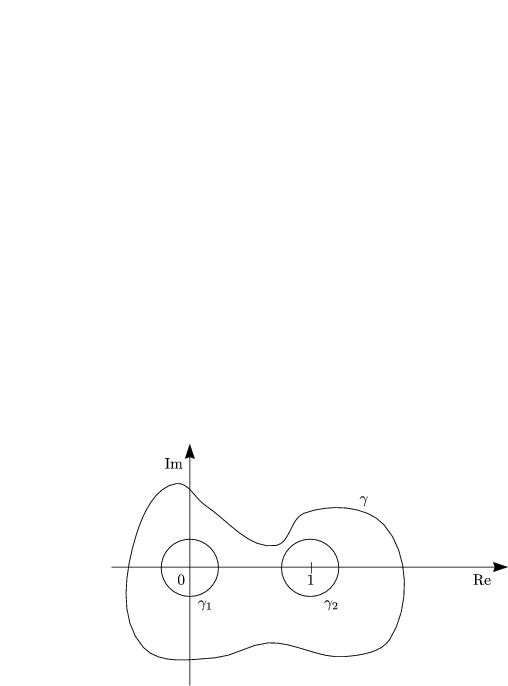
habe die Voraussetzungen von Satz 2 und umschließe die Punkte 0 und 1.

₁ und ₂ seinen genügend kleine Kreise um 0,1, die das äußere Gebiet nicht schneiden.

gf 2z - 1 gf 2z- 1 gf 2z- 1 z2---z dz = z2--z-dz + z2--z dz g g1 g2

Durch Partialbruchzerlegung folgt:

2z - 1 1 1 -2---= -+ ----- z - z z z - 1

gf gf gf gf dz- -dz-- dz- -dz-- z + z- 1+ z + z - 1= 4pi g1 - g1- -- g2 - g2-- -- 2pi 0 0 2pi

Satz 3 (Integralformel von Cauchy):

|----------------------------------------------------------------------------------------|
| |
|G (_ C sei ein beliebiges Gebiet, f : G '--> C sei holomorph. g < G sei geschlossene, doppelpunktfreie,
|positiv orientierte, st¨uckweise glatt Kurven, deren Innengebiet zu G geh¨ort. Dann gilt f¨ur jedes z in
|diesem Innengebiet: |
| gf |
| -1- f(z)- |
|f(z) = 2pi z- z dz |
| g |
-----------------------------------------------------------------------------------------

\text{[math]}

Wenn wir die Funktion f in Real- und Imaginärteil zerlegen, dann gilt die Potentialgleichung:

u + v = 0 xx yy

Die Formel im Satz wird in zwei Dimensionen angewendet, um diese Differentialgleichung zu lösen.

Beweis:

Mittels des Satzes 2 folgt:

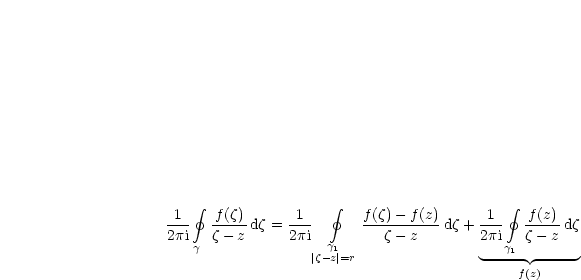
gf gf gf -1- f(z)- -1- f-(z)--f-(z) -1- f(z)- 2pi z- z dz = 2pi z- z dz + 2pi z- z dz g |z-gz1|=r --g1- ----- f(z)

gf lim 1-- f(z)--f(z)dz r'-->0 2pig q- z 1

Wir gehen auf die Definition des Linienintegrals zurück:

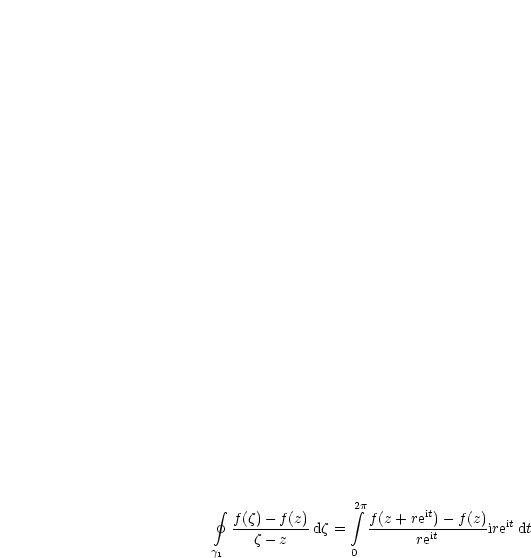
gf 2 integral p it f(z)--f(z)dz = f(z +-re-)--f(z)ireitdt g1 z- z 0 reit

2 integral p( ) Ir = i f(z + reit)- f(z) dt 0

| | || integral || || f(z) dz||< L¨ange von g .max |f(z)| ,z (- g |g |

| | |Ir|< 2pmax |f(z + reit)- f(z)| ,0 < t < p

Dies geht für r0 gegen 0 aufgrund der Stetigkeit von f.

Beispiel:

Mit dem Satz 2 folgt:

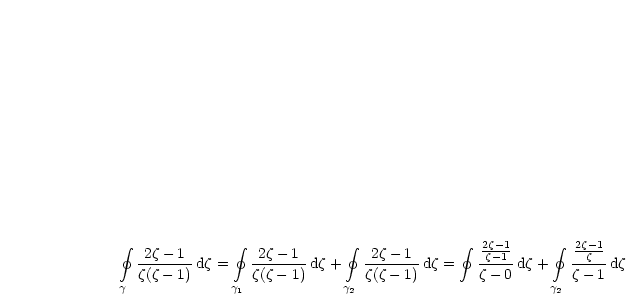
gf -2z--1- gf 2z---1- gf 2z---1- gf 2zz--11 gf 2z-z-1- z(z- 1) dz = z(z - 1) dz + z(z - 1) dz = z- 0 dz + z- 1 dz g g1 g2 g2

Nun ergibt sich mit Satz 3:

| | 2pi 2z--1|| + 2pi 2z--1-|| z- 1 |z=0 z |z=1

Beispiel:

f(z) =------1------ z(z -1)(z- 2)

gf f(z)dz g

Dieses Beispiels behandeln wir mit zwei Arten. Einmal mit Satz 2 und dann mit Satz 3.

Lösung mit Satz 2:

Durch Partialbruchzerlegung folgt wiederum:
$-----1-------= 1 1- --1--+ 1 -1--- z(z - 1)(z -2) 2 z z - 1 2 z- 2$

$gf gf g f g f gf g f gf 1dz- -dz-- 1 -dz-- f(z)dz = f (z)dz+ f(z)dz+ f(z)dz = 2 z + - z- 1+ 2 z- 2 = pi-2pi+pi = 0 g g1 g2 g3 g1 g2 g3$
Lösung mit Satz 3: $~f(z) =------1------ z(z- 1)(z- 2)$

$gf sum 3 gf ~f(z)dz = f~(z)dz g j=1gj$

$gf gf ----1--- ------dz----- = (z-1)(z-2)-dz z(z- 1)(z- 2) z- 0 g1 g1$

$z = 0, ~f(z) =----1----- (z -1)(z- 2)$
Somit folgt:
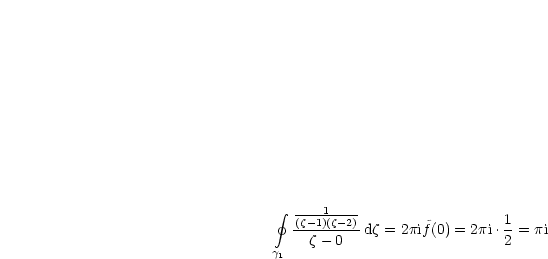
$gf (z--11)(z-2) 1 --z--0---dz = 2pi~f(0) = 2pi.2 = pi g1$
Die restlichen Integrale folgen dann analog, wobei wir dasselbe Endergebnis wie mit Satz 2 erhalten.

[prev] [prev-tail] [front] [up]