1.1 Einfache partielle Differentialgleichungen

Wie kann man überhaupt definieren, was eine Welle ist? Dabei handelt es sich um eine Störung, die sich zeitlich im Raum ausbreitet:

u = u(x1,x2,...,xn,t)

Gesucht sei also eine Funktion u(x,t) mit u_t(x,t) = 0, (x,t) ².
Alle Lösungen lauten hier folgendermaßen:
$u(x,t) = f(x)$
ist hierbei beliebig.
Gesucht sei eine Funktion u(x,t) mit u_xt(x,t) = 0, (x,t) ².
Wir wenden unsere obigen Erkenntnisse an:
$u (x,t) = f(x) x$
Durch nochmalige Integration folgt:
$integral x u(x,t) = f(s)ds +Y(t) = ~f(x)+ Y(t)$
und seien beliebig.

Nun kommt die Gleichung, mit der wir uns näher beschäftigen wollen. In Büchern findet man hierzu die Begriffe Wellengleichung, Transportgleichung und Advektionsgleichung. Gesucht ist u = u(x,t) mit u_t(x,t) - cu_x(x,t) = 0 mit c = const. > 0. Die Konstante c kann man hierbei als Geschwindigkeit interpretieren.

Erste Möglichkeit der Lösung:
Wir machen den Ansatz in Form einer Separation der Variablen (Separationsansatz, Variablentrennung):
$|---------------| |u(x,t) = f(x)g(t) ----------------$
Durch Einsetzen in die Differentialgleichung ergibt sich hierbei:
$f(x)˙g(t)- cf'(x)g(t) = 0$
Wir dividieren durch f(x) ^. g(t)0:
$f'(x)- 1˙g(t) f(x) = cg(t)$
Diese Gleichung muß nun für alle (x,t) gelten. Dies kann nur dann der Fall sein, wenn beide Seiten konstant sind:
$|-'--------------| |f(x)-= 1g˙(t)= c | -f(x)---cg(t)-----$
Wir bekommen also folgende Differentialgleichungen:
$f'(x) = cf(x) und g(t) = ccg(t)$
Die Lösungen dieser linearen Differentialgleichungen 1.Ordnung sind:
$f(x) = exp(cx) und g(t) = exp (cct)$
Also gilt durch Multiplikation der Einzellösungen:
$|-------------------------------------------| -u(x,t) =-f(x)g(t) =-exp(c-(x-+-ct))-mit c-=-const.$

Übung:

Versuche die Gleichung mit einem Summenansatz zu lösen:
$|-----------------| -u(x,t)-=-f(x)+-g(t)-$
Als Lösung erhält man dann:
$------------------------------ |u(x,t) = c(x +ct) mit c = const. ------------------------------|$

Sätzchen:

Beweis:

Durch Einsetzen in die Differentialgleichung folgt:
$' ' a(x,y).f (w(x,y))wx + b(x,y)f (w(x,y))wy = 0$
Mit Division durch '(w(x,y)) erhalten wir wieder obige Gleichung.

Lemma:

Es handelt sich um eine Eindeutigkeitsaussage.
Beweis:

$( ) ( ) x0 -c y(s) = t0 + s 1$
Es sei (x₀,t₀) ², t₀0. Zu zeigen ist dann u(x₀,t₀) = 0
$u(g) = u(x0- cs,t0 + s) = z(s)$

$z'(s) = -cux(x0- cs,t0 +s) +vt(x0- cs,t0 +s) = 0$

$z(s) = const.= z(0) = u(x ,t ) = z(-t ) = u(x + ct,0) = 0 0 0 0 0$

Satz 1:

Beweis:
- u(x,t) = (x + ct) ist Lösung von (*). Dies wurde schon gezeigt.
- Es sei u C¹(²) Lösung unserer Gleichung (*). Es ist dann zu zeigen, daß es ein C¹() gibt mit u(x,t) = . Definiere () := u(,0). Nachzurechnen ist nun: $u(x,t) = f(x+ ct) = u(x+ ct,0)$
  Wir betrachten hierzu:
  $v(x,t) = u(x,t) - u(x + ct,0)$
  Durch Differentiation folgt:
  $vt = ut- cux(x+ ct,0)$
  
  $cvx = cux- cux(x +ct,0)$
  
  $vt- cvx = ut- cux = 0$
  
  $v(x,0) = 0$
  v erfüllt daher die Voraussetzungen des Lemmas. Damit gilt v(x,t) = 0.
Wir wollen nun folgendes Anfangswertproblem lösen:
$u - cu = 0, (x,t) (- R2, u(x,0) = g(x) mit x (- R -t -x ug((xx,t+)=ct)$

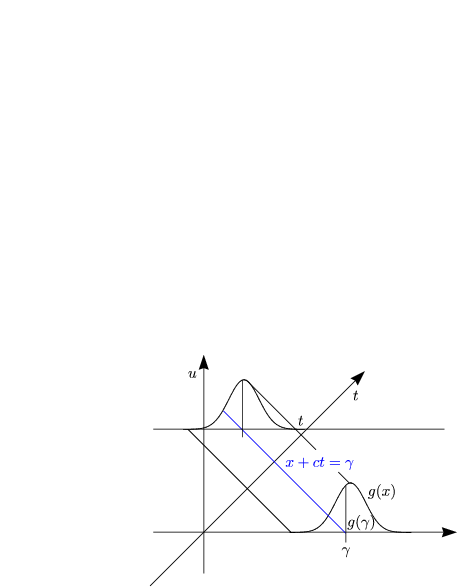
Durch u_t(x,t) -cu_x(x,t) = 0 wird eine sich nach links mit der Geschwindigkeit c unverzerrt ausbreitende Störung „beschrieben“(Welle).
Weitere Lösungsmöglichkeiten der Gleichung u_t(x,t) - cu_x(x,t) = f(x,t); (x,t) ², u(x,0) = g(x):
Die Funktion u sei Lösung. Wir betrachten z(s) = u(x - cs,t + s) und z(0) = u(x,t). Weiterhin gilt z(-t) = g(x + ct). Wir differenzieren dies nach s:
$' z (s) = ut(x- cs,t+ s)- cux(x- cs,t+ s) = f(x- cs,t+ s)$
Durch Integration erhalten wir dann:
$integral 0 integral 0 u(x,t)- g(x+ ct) = z'(s)ds = f(x - cs,t+ s)ds -t -t$
Damit folgt durch die Substitution s = t + s:
$|------------------------------------------------------| | integral t | |u(x,t) = g (x + ct) + f (x- c(s - t),s) ds mit p(x,0) = 0 | --- --- | | dAellre h Lo¨osmuongegnenen 0-------- --------- | | Gleichung deSrp ienhzioelmleogL¨oenseunn Ggpl(exic,thu)ng | -------------------------------------------------------$

Wir machen die Probe:

integral t u = g'(x+ ct)+ f (x+ c (t- s),s) ds x x 0

integral t cux = cg'(x +ct)+ c fx (x + c(t- s),s) ds 0

t ' integral ut = cg(x+ct)+f (x,t)+c fx (x + c(t- s),s) (Differentiation von Parameterintegralen) 0

Durch Subtraktion folgt dann:

|---------------| ut--cux-=-f(x,t)--

Wir formulieren außerdem das Problem P(f,g), das gegeben ist durch:

|------------------------------------| | ut(x,t)- cux(x,t) = f(x,t) | | { | |P (f,g) = u(x,0) = g(x) | | | -------------------------------------

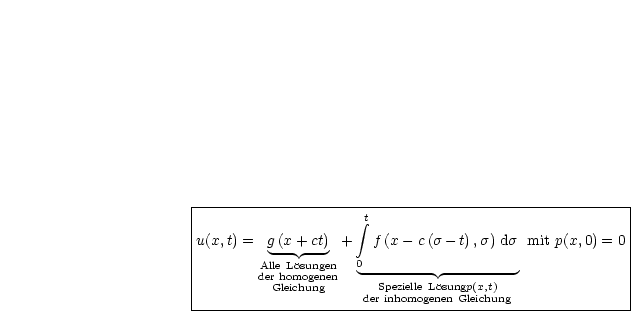
P(f,g) ist nun linear, wenn aus u₁ löst P(f₁,g₁) folgt, daß auch u₂ das Problem P(f₂,g₂) löst. Oder anders formuliert: u₁ + u₂ löst das Problem P(f₁ + f₂,g₁ + g₂) mit , . Man nennt dies auch das Superpositionsprinzip. Betrachten wir nun also unsere Gesamtlösung:

u₁(x,t) = g(x + ct) löst P(0,g).
Es handelt sich also um die homogene Lösung.
u₂(x,t) = ₀^tf(x + c(t - s),s)ds löst P(f,0).
Wir haben hier die inhomogene Lösung.

Wir notieren uns nochmal das wichtige Lemma von vorher:

Folgerung:

Lösen u₁, u₂ das Problem P(f,g), dann gilt u₁ = u₂. Dies folgt aus dem Lemma, da u₁ - u₂ das Problem P(0,0) löst. P(f,g) ist infolgedessen eindeutig lösbar.