1.2 Wellengleichung

Wir betrachten folgende inhomogene lineare partielle Differentialgleichung zweiter Ordnung.

f(x,t) kann man immer als Wirkung von außen, die auf das System wirkt, interpretieren. Hat u die Einheit cm und t die Einheit s, so könne wir c als Geschwindigkeit interpretieren.

• 1.Möglichkeit:

  Wir bezeichnen im folgenden die erste partielle Ableitung nach t mit _t und die erste partielle Ableitung nach x mit _x. Damit gilt also:

  

  Die partielle Differentialgleichung zerfällt somit in zwei verschiedene Differentialgleichungen 1.Ordnung:

  • v_t - cu_x = f(x,t)

    Hieraus können wir v mit Satz 2 berechnen.

  • u_t + cu_x = v(x,t)

    Aus dieser Gleichung folgt dann u mit Satz 2.

  Damit gilt also:

  

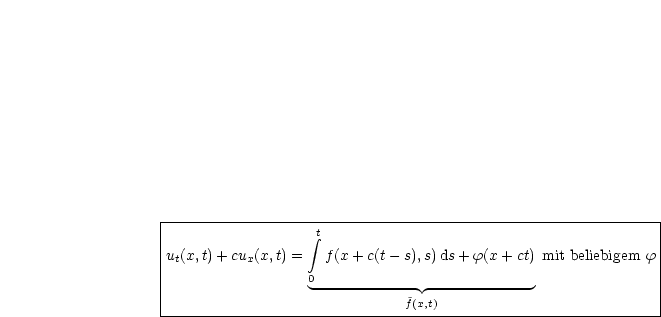
  Mit Satz 2 kann dann die Lösung u(x,t) hingeschrieben werden. Als Übungsvorschlag kann man folgende Gleichung so behandeln:

  

• 2.Möglichkeit:

  Vorgehen:

  Wir zerlegen das Problem in P₁ und P₂. Aus P₁ resultieren dann alle Lösungen der homogenen Gleichung:

  

  Mit P₂ bestimmen wir eine Lösung der inhomogenen Gleichung:

  

  Durch Addition folgt dann die gesamte Lösung. Mit der vorherigen Zerlegung ergibt sich:

  
  
  

  Aus der zweiten Gleichung erhalten wir mit Satz 1:

  

  Durch Einsetzen in die erste Gleichung ergibt sich:

  

  Mit dem Beispiel von vorher folgenden dann alle Lösungen:

  

  Wir können die Funktion umschreiben, indem wir das Integral auseinanderziehen:

  

Satz 3:

Es soll folgendes Anfangswertproblem gelöst werden:

Die Differentialgleichung ist invariant gegen die Transformation t- t. Wir notieren uns nochmal:

• v(x,t) = (x + ct)
• u_t(x,t) + cu_x(x,t) = (x + ct)

Bestimme und , so daß die Anfangsbedingungen erfüllt sind. Widmen wir uns der ersten Bedingung:

Durch Einsetzen von t = 0 in die zweite Gleichung erhalten wir:

Dann ergibt sich mit der Lösungsformel:

Damit folgt dann noch durch eine kleine Umformung die D'ALEMBERTsche Formel:

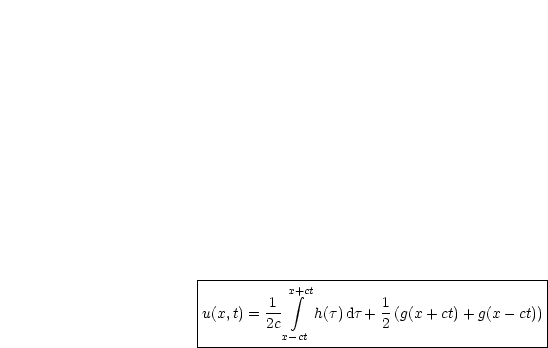
Das ganze wird zum Schluß noch als Satz formuliert.

Satz 4:

Übung:

• Führe die Probe durch!
• Interpretiere anschaulich die folgenden Fälle:
  • h = 0, g(x)0 für x₁ < x < x₂
  • h(x)0 für x₁ < x < x₂, g(x) = 0

Wir betrachten nochmals:

Wir können eine Lösung (x,t) von (*) sofort angeben:

Diese Funktion ist uns aber zu trivial. Wir verwenden daher den Ansatz:

Wir leiten dies ab:

Durch Einsetzen in die Differentialgleichung erhalten wir dann:

Es gibt zwei Möglichkeiten:

• ''(a₁x + a₂t) = 0

  Diese Lösung liefert uns nichts neues.

• a₂² - c²a₁² = 0

  Dies liefert uns folgende Beziehung:

  

  Mit a₁ = 1 erhalten wir a₂ = ±c.

Daher erhalten wir

Wir bekommen also das Ergebnis, welches wir früher schon auf anderem Wege erhalten haben.

Geometrische Interpretation:

Wir betrachten den Fall für h = 0 und g0 auf einem kleinen Intervall auf der x-Achse. Als konkretes Beispiel nehmen wir:

Also gilt:

Spezielle Lösung:

Wir betrachten:

1.2.1 Methode von DUHAMEL

Wir führen damit auf viele Probleme des vorhergehenden Typs zurück. s > 0 sei fest. Wir betrachten nun folgendes Problem:

Wir müssen dieses Problem auf die Zeit t = 0 transformieren, damit wir die D'ALEMBERTsche Formel anwenden können. v = v(x,t) sei Lösung von (*). Dann ist w(x,t) := v(x,t + s) Lösung folgenden Problems:

Ist w = w(x,t) Lösung von (**), so ist v(x,t) := w(x,t-s) Lösung von (*). Damit gilt:

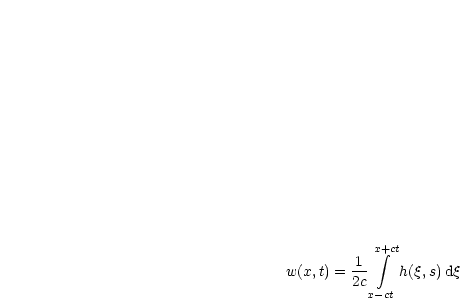
Damit erhalten wir als Lösung von (*) für t > s > 0:

Wir nennen diese Lösung im folgenden u(x,t;s). Es soll gezeigt werden, daß u(x,t) das Problem (* * *) löst:

Es gilt trivialerweise u(x,0) = 0. Durch einmaliges Differenzieren folgt:

Wir differenzieren zum zweiten mal:

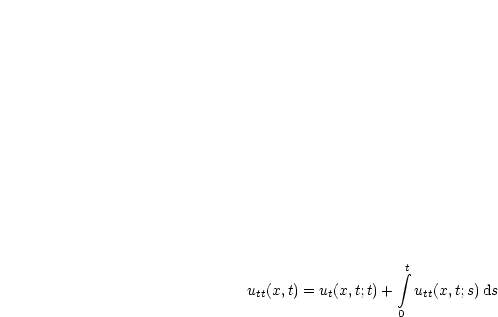
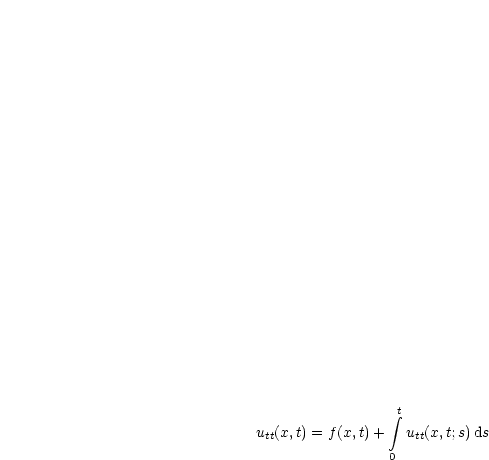
Durch Subtraktion folgt:

Es kann außerdem gezeigt werden, daß dies die Lösung des inhomogenen Problems darstellt:

Wir machen nun die Substitution s = t - s, womit gilt:

Dies ist die Lösung des Problems:

Übung:

Es sei f(x,t) = xt. Dann ist eine Lösung des Problems gegeben durch: