1.8 Kontinuittsgleichung

1.8 Kontinuitätsgleichung

Diese beschreibt die Erhaltung der Masse einer strömenden Flüssigkeit. Dazu sei ein beschränktes Gebiet G ³ gegeben. G befindet sich außerdem innerhalb der strömenden Flüssigkeit und G sei die Oberfläche von G. Dei Dichte der Flüssigkeit sei (,t); die Strömungsgeschwindigkeit wird mit = (,t) bezeichnet.

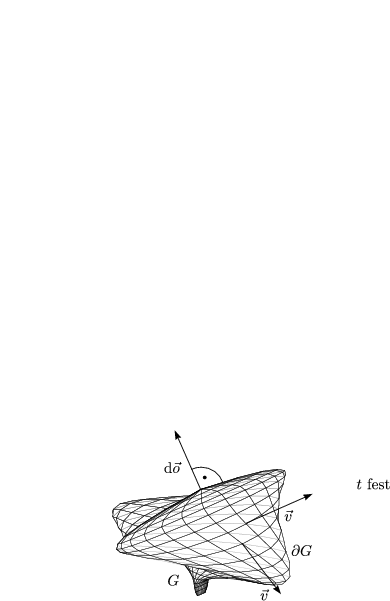
Durch Integration über die Dichte erhalten wir die Masse der Flüssigkeit innerhalb des Gebietes:

integral M = r(r,t)dt G

M ändert sich, wenn Flüssigkeit durch G in G oder aus G herausströmt. Während der Zeitspanne dt ändert sich M wie folgt:

|--------------------------| | integral | |DM = - dt r(r,t)v(r,t).do | ----------@G---------------

Leiten wir die obigen Formel für die Masse zeitlich ab, so erhalten wir:

integral DM = dt rt(r,t)dt G

Durch Gleichsetzen folgt also:

integral integral r (r,t)dt+ r(r,t)v(r,t).do = 0 t G @G

Mittels des Gaußschen Satzes erhalten wir dann wieder:

integral -[----------------------]-------| | rt(r,t)+ \~/ .(r(r,t))v(r,t) dt = 0| G | -----------------------------------

Also folgt die Kontinuitätsgleichung:

|--------------------------| | \~/ .(r(r,t)v(r,t))+ rt(r,t) = 0 ---------------------------

1.8.1 Erhaltungssatz

Die zeitliche Änderung der Gesamtmenge einer physikalischen Größe (gegeben mittels einer Dichtefunktion/Konzentration u(,t)), die in einem Raumbereich G enthalten ist, rührt her vom Fluß (,t) dieser Größe durch den Rand G von G und der Geschwindigkeit, mit der die Größe im Gebiet erzeugt oder vernichtet wird (beschrieben durch f(,t,u(,t)):

integral integral integral d- u(r,t)dt = f(r,t).do + f (r,t,u(r,t)) dt dtG @G G

Die Gleichung sieht dann im allgemeinen Fall so aus:

ut(r,t)+ \~/ .f(r,t)= f (r,t,u(r,t)) - - f=rv

u = r, f = 0

r = r(r(t),t)

Durch Anwendung der Kettenregel ergibt sich:

-dr(r(t),t) = rt + \~/ r(r(t),t).v dt

Des weiteren gilt:

\~/ .(rv) +r = 0 t

\~/ r .v+ r \~/ .v+ rt = 0

Durch Einsetzen erhalten wir dann:

\~/ r .v + r \~/ .v+ d-r(r(t),t) - \~/ r .v = 0 dt

Damit folgt dann schließlich:

|-------------------| | 1 d | divv = -r dtr(r(t),t) | --------------------

1.8.2 Verkehrsfluß

u(x,t) = (x,t) sei die Verkehrsdichte (=Anzahl der Autos pro Längeneinheit) und (x,t) = q(x,t) sei die Flußgeschwindigkeit des Verkehrs, also die Anzahl der Autos pro Zeiteinheit, die zur Zeit t den Punkt x passieren. f = 0 bedeutet, daß Autos die Straße nicht verlassen und auch keine neue Autos hinzukommen. [x₁,x₂] sei ein Stück der Autobahn. Die Gesamtzahl der Autos auf diesem Abschnitt ist gegeben durch:

integral x2 x1 r(x,t)dx

Für die Zahl der Autos pro Zeiteinheit, die zur Zeit t bei x₁ auf das Stück [x₁,x₂] fahren minus die Zahl der Autos die bei x₂ das Stück [x₁,x₂] verlassen.

x x d integral 2 integral 2 dt r(x,t)dx = rt(x,t)dx x1 x1

Man kann dies auch schreiben als:

x integral 2 q(x1,t)- q(x2,t) = - qx(x,t)dx x1

Damit erhalten wir durch Gleichsetzen:

|------------------| -rt(x,t)+-qx(x,t) =-0|

Es ist q = G((x,t), die Flußgeschwindigkeit hängt also von ab. Damit gilt:

' qx = G (r(x,t)rx

Damit erhalten wir eine nichtlineare partielle Differentialgleichung erster Ordnung:

|---------'----------------| -rt(x,t)+-G-(r(x,t))rx(x,t) =-0

Beispiel:

( ) -r q = gr 1- r1

sei die mittlere freie Geschwindigkeit und ₁ das Maximum der Autodichte. Außerdem kann man noch einen Korrekturterm aufgrund eines Bremseffekts unter Zunahme der Dichte berücksichtigen:

( ) q = qr 1- -r - krx mit k > 0 = const. r1

Durch Einsetzen dieser Funktion in die partielle Differentialgleichung erhalten wir:

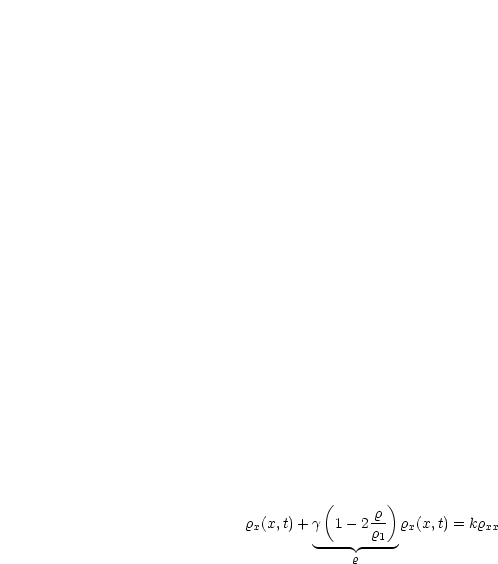
( r) rx(x,t)+ g 1- 2r- rx(x,t) = krxx ---- --1- r

k_xx nennen wir Viskositätskorrektur.

rt + rrx = krxx

Diese Gleichung nennt man Burger’s Gleichung (Modell für kompressible Flüssigkeiten).

[prev] [prev-tail] [front] [up]