1.7 Bemerkungen zu Maxwellschen Gleichungen

Wir benötigen hier folgenden Entwicklungssatz eines doppelten Kreuzproduktes:

Damit folgt dann:

Es sei nun = (,t) und = (,t). Damit notieren wir uns die vier Maxwellschen Gleichungen:

• × = -_t
• × = _t +
• ^. =
• ^. = 0

Es seien , , und = const. Mit der dritten Maxwellschen Gleichung folgt:

Darüber hinaus gilt unter Verwendung der zweiten Gleichung:

Damit erhalten wir schließlich durch Gleichsetzen:

Analog gilt:

Diese nennt man auch Telegraphengleichung.

1.7.1 Telegraphengleichung

Wir stellen uns vor, daß wir einen langen Leiter haben. Durch diesen Leiter fließe ein Strom i = i(x,t) und es herrsche eine Spannung v = v(x,t). In diesem Leiter sollen die Größen R (Widerstand), L (Induktivität), C (Kapazität) und G (Verlustkoeffizient) gleichmäßig verteilt sein. Dann gilt für die Spannung mittels des Ohmschen Gesetzes:

Nach dem Gesetz über Ladungserhaltung gilt außerdem:

Wir differenzieren die erste Gleichung nach x:

Außerdem differenzieren wir die zweite Gleichung nach t und multiplizieren sie mit L:

Durch Subtraktion dieser beiden Gleichung folgt:

Durch Einsetzen der obigen zweiten Gleichung erhalten wir dann schließlich:

Wir verwenden nun folgende Bezeichnungen:

Der Term au_t ist Gleichung (1) nennt man dissipativen Term. Zur Lösung machen wir folgenden „Separationsansatz“:

Allgemein gilt (siehe HM I);

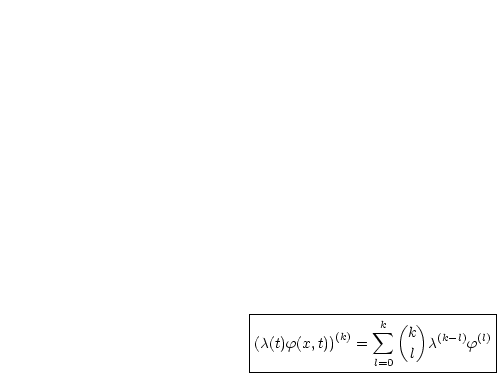
Damit folgt dann für k = 2:

Der Zeitableitung _t soll herausfallen. Damit haben wir folgende gewöhnliche Differentialgleichung 1.Ordnung:

Die Lösung können wir einfach angeben (siehe HM I);

Damit folgt dann:

Durch Einsetzen erhalten wir wieder:

Unser 1.Ergebnis ist: u(x,t) = exp(x,t) = exp(x,t) ist Lösung, falls = (x,t) Lösung von (2) ist. Für A = 0 haben wir:

Hierbei handelt es sich um eine gedämpfte Welle, die relativ unverzerrt ist. Im Falle A = 0, also RC = GL kann man gute Signale aussenden. Für A0 () versuchen wir Lösungen in Form fortschreitender ebenen Wellen darzustellen:

Durch Einsetzen in die Gleichung erhalten wir:

Daraus sieht man, daß F = 0 gelten muß, da A0. Lösungen in der Form (x,t) = F(x - ct) gibt es also nicht, der Ansatz ist unbrauchbar. Wir versuchen es mit einem neuen Ansatz:

Durch Einsetzen erhalten wir:

Wir setzen x - t = und dividieren durch ² - c²:

Lösungen dieser Differentialgleichung 2.Ordnung sind:

Wir erhalten weitere Lösungen durch Superposition:

Überlagerung von Wellen verschiedener Geschwindigkeit führen zu Dispersion. Wir notieren uns nochmals:

Wir lösen nach c(k) auf:

Falls die Ausbreitungsgeschwindigkeit von k (oder auch ) abhängen, spricht man von Wellendispersion. Eine Differentialgleichung heißt dispersiv, falls sie Lösungen der Form exp besitzt mit = (k) mit ''(k)0. Im Fall (k) heißt die Differentialgleichung diffusiv. Dazu wollen wir die Wärmeleitungsgleichung untersuchen:

Durch Einsetzen des obigen Ansatzes erhalten wir:

Daraus folgt = -iDk² . Dies Gleichung ist also diffusiv.

Zusammenfassung:

Wir haben uns beschäftigt mit:

• Schwingende Saite
• Umformung der Maxwellgleichungen

  Dies führte dann zur Telegraphengleichung.

• Lösung der Telegraphengleichung
• Erhaltungsaussagen (Conservation Laws) der Physik

  Damit wollen wir uns jetzt beschäftigen.