1.6 Die schwingende Saite

u(x,t) bezeichnet die Auslenkung aus der Ruhelage a der Stelle x zur Zeit t. (x) sei die Dichte der Saite. (x,t) sei die Dichte der Kraft, die von außen vertikal auf die Stelle zur Zeit t wirkt.

u(0,t) = 0 = u(l,t) A t

Gegeben sei u(x,0). Gesucht sei dann u(x,t):

(H(x, t)) T(x,t) = V(x,t)

sei die Kraft an der Stelle x zur Zeit t, die von der Spannung herrührt. Diese Kraft wirkt tangential. Die Tangentenrichtung (x,t) sei gegeben durch:

( 1 ) t(x,t) = ux(x,t)

T(x,t)× t(x,t) = o ==> V (x,t) = H(x,t)u (x.t) x

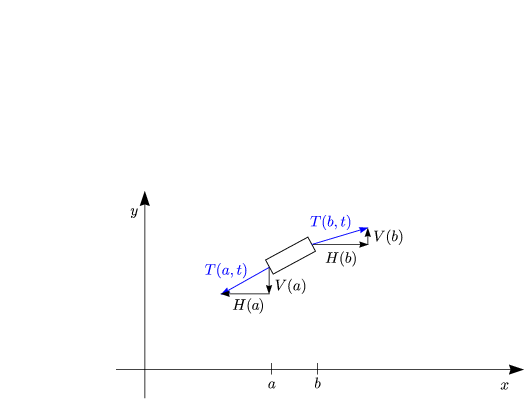
(x,t) sei die Kraftdichte und (x) die Massendichte der Saite.

H(a,t) = H(b,t) = H = const.

Die Kraft auf die Saite ergibt sich nun zu:

b b integral integral H (ux(b,t)- ux(a,t))+ f(x,t)dx = rutt(x,t)dx a a

Damit folgt daraus:

integral b [H .uxx(x,t)+ f(x,t)- r(x)utt(x,t)] dx = 0 a

Da dies für alle Stelle x und t gelten muß, haben wir (Widerspruchsbegründung oder Mittelwertsatz):

|---------------------------------- V~ --| | -H-- f(x,t)- H-| |utt(x)- r(x)uxx(x,t) = r(x) mit c = r | ----------------------------------------

Im Falle n = 3 gilt:

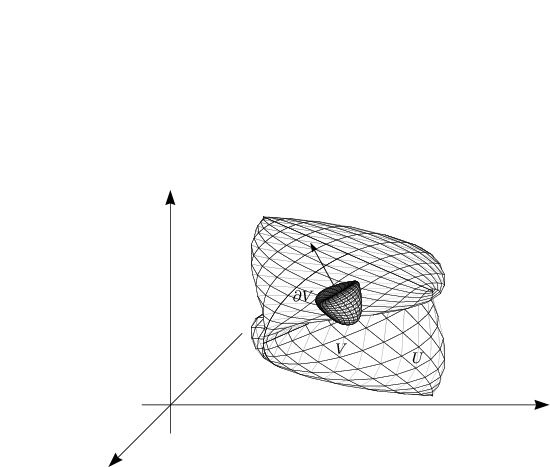
In diesem Falle sei x ein Punkt im Dreidimensionalen. U ³ sei elastisch. V U ist das Volumen und V die Oberfläche des Körpers.

integral integral r(x)utt(x,t)dt = - F .n do V @V

Mit dem Gaußschen Satz ergibt sich dann:

integral integral r(x)utt(x,t)dt = - \~/ .F dt V V

Daraus folgt dann:

|----------------------------| | integral ( ) | | r(x)utt(x,t) + \~/ .F dt = 0| -V---------------------------

Auch hier muß dann gelten wie zuvor:

|------------------------| r(x)utt(x,t)+- \~/ -.F(x,t) =-0

Oft gilt, daß die Kraft nur vom Gradienten von u abhängig ist.

( ) F = F \~/ u

Unter Vernachlässigung höherer Terme, also mit einer Linearisierung folgt:

( ) F \~/ u ~ ~ -a \~/ u

Was hier dahinter steckt, ist das Hookesche Gesetz. a ist eine Konstante, die von den elastischen Eigenschaften des Körpers abhängig ist. Damit erhalten wir:

|----------------| -r(x)utt--a /_\ u-=-0|

[next] [prev] [prev-tail] [front] [up]