4.1 Nachtrag zu [stark] konvexen Funktionen

Vorbereitungen:

Betrachten wir h C²(I) mit dem Intervall I und a, b I.

integral b integral b integral b h(b)- h(a) = 1.h'(t)dt = [(t- b)h'(t)]ba- (t-b)h''(t )dt = (b- a)h'(a)+ (b-t)h''(t)dt a a a

h(b) - h(a) = (b - a)h'(a) + _a^b(b - )h''()d
Mit b = 1 und a = 0 folgt dann:
h(1) - h(0) = h'(0) + ₀¹(1 - )h''()d
Setzen wird b = p + und a = p, so gilt außerdem:
h(p + ) - h(p) = h'(p) + _p^p+(p + - )h''()d
Es sei U ⁿ offen und konvex. Außerdem sei f : U zweimal stetig differenzierbar. x und x+y seien U, womit mittels der Konvexität folgt, daß {x + ty,0 < t < 1} U. Betrachte nun:
$h(t) = f(x+ ty) mit t '--> x + ty '--> h(t)$
Wir bezeichnen (t) = x + ty mit : ⁿ.
$h(t) = (f o f)(t)$
Dann berechnen wir h'(t) und h''(t).
$' ' ' ' h(t) = f (f(t))f(t) = \~/ f (f(t))f (t) = \~/ f (x+ ty).y$
Die zweite Ableitung schreiben wir mittels der HESSEmatrix:
$'' T sum n h (t) = y Hf (x+ ty)y = fxjxk(x + ty)yjyk j,k=1$
Gleichung (2) für h(t) = f(x + ty) mit x,x + y U U ⁿ ergibt dann:
f(x + y) - f(x) = $\~/$ f(x) ^. y + ₀¹(1 - )y^TH_f(x + y)y d

Satz 5:

|----------------------------------------------------------------------------------------|
| |
|Es sei f = f(x,p) und fp seien definiert und stetig auf [a,b]× I. Es gelte fpp(x,p) > 0 f¨ur jedes x (- [a,b]
|und alle p (- I. Dann ist f = f(x,p) auf [a,b]× I bez¨uglich p [stark] konvex. |
-----------------------------------------------------------------------------------------

Beweis:

Unser Ziel ist, folgendes zu zeigen:

f(x,p+ y) -f (x,y) > fp(x,p)y

Setze in (3) h(p) = f(x,p) ein:

p integral +y f(x,p+ y) -f (x,p) = yfp(x,p)+ (p+ y - t)fpp(x,t)dt p -------!-- ---------- >0 f¨ur y/=0

Fall 1: > 0
Dann ist das Integral auf jedem Fall > 0 und der Satz ist für diesen Fall gezeigt.
Fall 2: < 0
Wir drehen einfach die Integrationsgrenzen um:
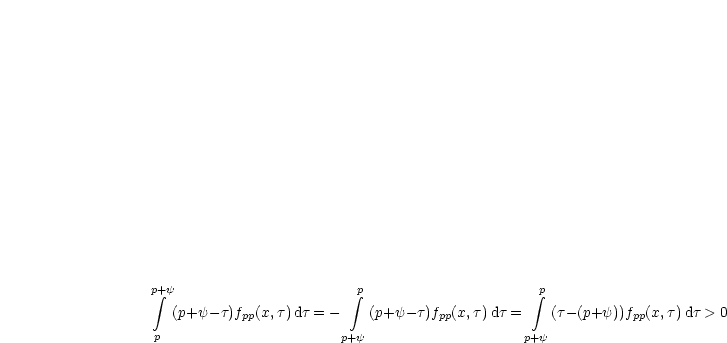
$p integral +y integral p integral p (p+y - t)fpp(x,t)dt = - (p+y -t)fpp(x,t)dt = (t-(p+y))fpp(x,t )dt > 0 p p+y p+y$

Beispiel:

Gegeben sei folgende Funktion:

f(x,p) = V~ 1-+-p2

Wird dies zweimal nach p differenziert, so gilt f_pp(x,p) > 0, womit Konvexität gewährleistet ist. Analog gilt dies auch für:

V~ ---------- f(x,z,p) = 1+ z2 + p2

Satz 6:

|----------------------------------------------------------------------------------------|
| |
|f = f (x,z,p) sei definiert auf [a,b]× U U (_ R2 (konvexes Gebiet) und dort zweimal stetig differenzierbar.
|Die HESSEmatrix von f bez¨uglich z, p sei f¨ur alle x (- [a,b] und alle (z,p) (- U positiv semidefinit. Dann
|ist f bez¨uglich (z,p) konvex. |
-----------------------------------------------------------------------------------------

Beweis:

Eine (m,n)-Matrix ist positiv (semi)definit, wenn A = A^T und q(x) = x^TAx = _j,k=1a_jkx_jx_k > 0 x ⁿ (positiv semidefinit) und > 0 x0 (positiv definit). Wir betrachten:

! f(x,z + f,p+ y) - f(x,z,p) > fz(x,z,p)f+ fp(x,z,p)y

Mit der Beziehung (3) ergibt sich dann:

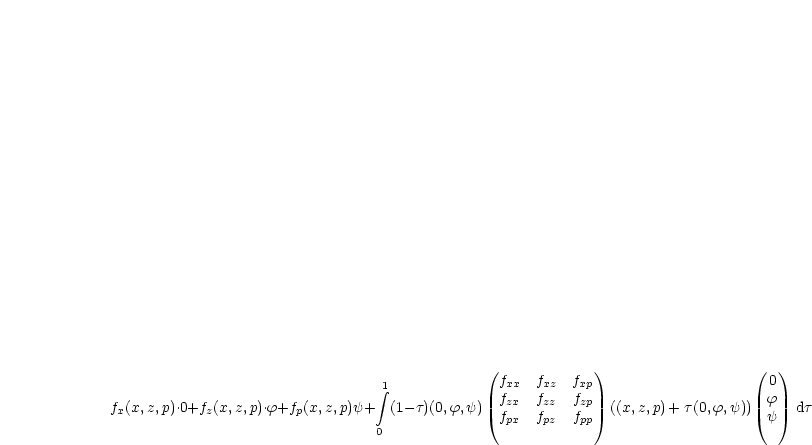
( ) ( ) integral 1 fxx fxz fxp 0 fzx fzz fzp f fx(x,z,p).0+fz(x,z,p).f+fp(x, z,p)y+ (1- t)(0,f,y) fpx fpz fpp ((x,z,p)+ t(0,f,y)) y dt 0

Man kann dies nun schreiben als:

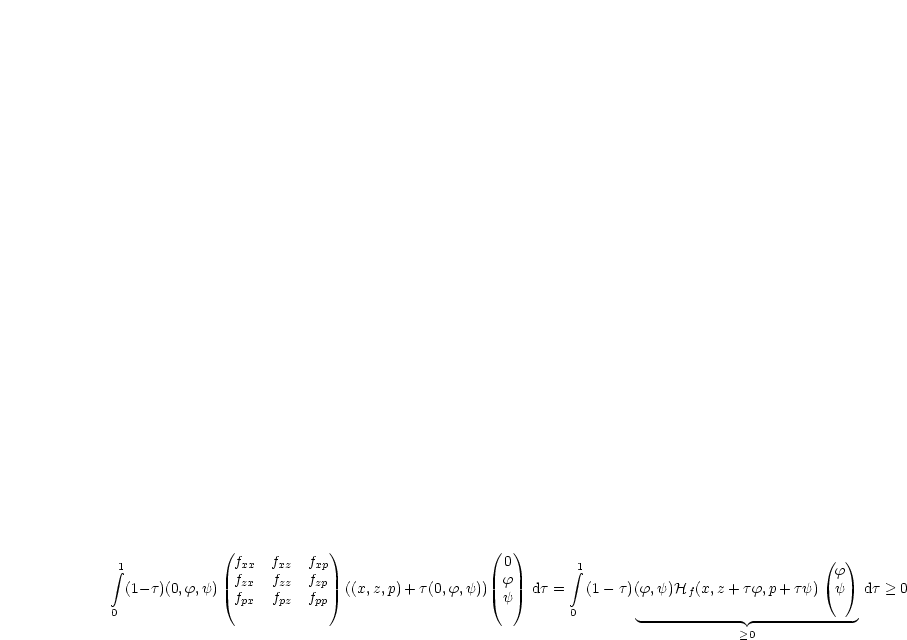
( ) ( ) integral 1 fxx fxz fxp 0 integral 1 (f ) (1- t)(0,f,y) fzx fzz fzp ((x,z,p) +t (0,f,y)) f dt = (1 -t) (f,y)H (x,z + tf,p +ty) y dt > 0 fpx fpz fpp y f 0 0 ------------- ------------- >0

Damit ist die Aussage bewiesen.

Wir werden die Definitheit nun folgendermaßen nachprüfen. Betrachten wir hierzu folgende Matrix A:

( ) a b A = b c

A ist positiv semidefinit (definit), falls a > 0, ac - b² > 0 (a > 0, ac - b² > 0) gilt.

Beispiel:

Betrachten wir:

f(x,z,p) = V~ 1-+-z2 +-p2

Hier folgt dann einfach:

fzz > 0, fzzfpp- f2zp > 0

Damit ist die Funktion konvex.

Beispiel:

V~ ------- f(x,z,p) = z2 + b2p2 mit b /= 0

Wir hatten hierzu beispielsweise die Funktion f(x) = ||x|| betrachtet und damals festgestellt, daß diese konvex in ⁿ{0} ist. Berechnen wir also:

fzz > 0, fzzfpp- f2zp = 0

Damit ist die HESSEmatrix positiv semidefinit und f ist nach Satz 6 bezüglich (z,p) konvex für (z,p)(0,0). f ist nicht stark konvex, da die Matrix den Eigenwert Null besitzt nach det(A) = ₁ ^. ₂ ^. ..._n. Man kann dies jedoch auch anders machen. Zu untersuchen ist dann:

zf-+-b2py- V~ ------2---2------2 V~ -2---2-2 V~ z2-+-b2p2-< (z + f) + b (p+ y) - z + b p

Gleichheit (und damit starke Konvexität) gilt nur, falls ^. = 0 ist. Wir multiplizieren die Ungleichung mit dem Nenner > 0 durch:

zf + b2py+ z2 +b2p2 < V~ z2-+-b2p2 V~ (z-+-f)2 +-b2(p+-y)2

Den rechten Term kann man als Länge eines Vektors interpretieren.

|| || || || ||||( z )|||| ||||( z + f ) |||| zf + b2py + z2 + b2p2 < |||| bp |||| |||| b(p+ y) |||| || || || ||

Dann formt man die linke Seite um:

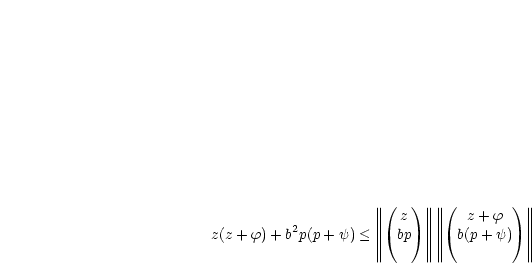
||( ) || ||( ) || |||| z |||| |||| z + f |||| z(z +f) + b2p(p+ y) < |||| bp |||| |||| b(p+ y) |||| || || || ||

Die linke Seite stellt nun gerade ein Skalarprodukt dar:

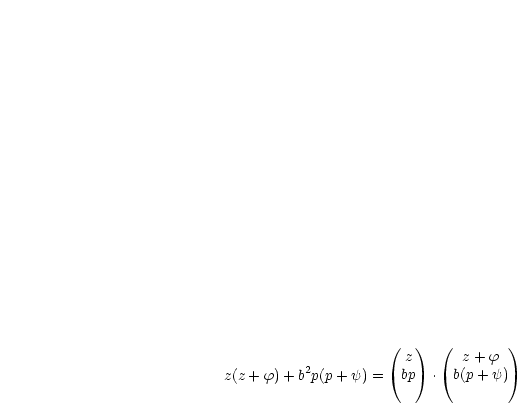
( ) ( ) 2 z z + f z(z + f)+ b p(p+ y) = bp . b(p + y)

Damit stellt die obige Ungleichung nichts anderes als die Schwarzsche Ungleichung bezüglich der beiden Vektoren dar. Gleichheit gilt nur, falls beide Vektoren linear abhängig sind:

(z + f) (z ) p +y = c p

z(c - 1) = f und p(1- c) = y

Setzen wir beispielsweise = 2, dann erhalten wir = z und = p. Damit ist die Funktion nur konvex.

Weitere Regeln für Konvexität:

Starke Konvexität bezieht sich immer auf die Variablen z und p:

stark konvex + konvex = stark konvex
positive Funktion von x ^. stark konvex = stark konvex
f(x,z,p) = (x) + (x)z + (x)p ist konvex (nicht stark konvex).

Beispiel:

Betrachten wir:

V~ ------ f(x,z,p) = -2(sin(x))z + p2 + x2 1+ z2

In einem früheren Beispiel hatten wir nachgewiesen, daß p² stark konvex ist. Für den ersten Term liegt nach Regel (3) Konvexität vor. Da beim dritten Term stark konvex ist, ist auch der x² stark konvex und damit auch der gesamte Ausdruck.

[front] [up]