4 Konvexe Funktionale

Kapitel 4
Konvexe Funktionale

4.1 Nachtrag zu [stark] konvexen Funktionen

Definition:

|----------------------------------------------------------------------------------------|
|F: D < Y '--> R sei Funktional. F heiß t auf D konvex [strikt konvex], falls aus y und y+ v folgt, daß
|dF(y;v) existiert und F (y+ v)- F(y) > dF (y;v). [Gleichheit gilt nur fur v = 0.] |
| ¨ |
-----------------------------------------------------------------------------------------

Satz 1:

|----------------------------------------------------------------------------------------|
|Es sei F auf D [strikt] konvex. Dann minimiert jedes y (- D, f¨ur das dF (y ;v) = 0 A y + v (- D gilt, F
|auf D [eindeutig]. 0 0 0 |
| |
-----------------------------------------------------------------------------------------

Beweis:

Es sei y beliebig. Unser Ziel ist es zu zeigen, daß F(y) -F(y₀) > 0. Setze hierzu v = y - y₀. Dann folgt hieraus y = y₀ + v. Dann können wir die Definition anwenden:

F (y)- F(y0) > dF(y0,v) = 0

Wenn v0 ist, gilt das Gleichheitszeichen.

Beispiel:

Y = C[a,b], , C[a,b], (x) > 0 für x [a,b] $integral b[ ] F (y) = r(x)y2(x)+ b(x)y(x) dx a$
Es ist das Minimum auf zu berechnen:
$integral b dF (y;v) = [fz .v + fp .v'] dx a$
Es gilt hier n = 1, da es sich um ein skalares Feld handelt. Außerdem gilt N = 1, da wir nur die Variable x haben. (v(x) )
$2 f (x,z,p) = r(x)z + b(x)z, fp = 0, fz = 2r(x)z + b(x)$
Für unser Integral benötigen wir nun:
$' fz(x,y(x),y(x)).v(x) = 2r(x)y(x) .v(x)+ b(x) .v(x)$

$integral b dF(y;v) = [2r(x)y(x).v(x)+ b(x).v(x)] dx a$
Schauen wir uns nun die Konvexität des Funktionals an:
$integral b[ ( ) ] F(y+ v) -F (y) = r(x) y2 + 2yv+ v2 + b(y +v) - r(x)y2- by dx = a integral b = r(x)v2(x)dx + dF(y,v) > dF (y;v) a$ (4.1)

Gleichheit gilt nur für v = 0. F ist strikt konvex auf = Y = C[a,b]. Nach Satz 1 ist y₀ aus F(y₀;v) = 0 v Y zu berechnen.
$b integral [ 2 ] F(y) = r(x)y + b(x)y dx a$

$integral b dF (y0;v) = [2r(x)y0(x)v(x)+ b(x)v(x)] dx = 0 A v (- C[a,b] a$

$integral b dF (y0;v) = [2r(x)y0(x)+ b(x)]v(x)dx = 0 a$
Nach einem der Fundamentalsätze der Variationsrechnung folgt, daß der Klammerausdruck gleich Null ist:
$|-------------------------| |y0(x) = - b(x)-fu¨r a < x < b ----------2r(x)-------------$
F(y) = _a^b dx
Dieses Funktional soll minimal werden auf = {y C[a,b], y(a) = a₁, y(b) = b₁} mit a₁² + b₁²0. Mit y und v Y gilt y + v .
$v (- D0 = {~y (- C[a,b]| ~y(a) = ~y(b) = 0}$
Es genügt, den Störterm, welcher nur von x abhängt, wegzulassen und den restlichen Ausdruck zu untersuchen:
$b integral 2 F (y) = y 8x)dx a$

$F (y+ v)- F(y) > dF (y;v) A v (- D 0$
Dies gilt auf jeden Fall, da dies nach Beispiel 1 mit = 1 und = 0 so ist. Gleichheit gilt genau dann, wenn:
$integral b v2(x)dx = 0 a$
Es resultiert also v = 0 ₀; F = F(y) ist auf strikt konvex. Nach Satz 1 ist F(y₀,v) = 0 v ₀ zu lösen.
$integral b 2 y(x)v(x)dx = 0 A v (- D 0 0 a$
Daraus folgt y = y₀(x) = 0 x, womit das Problem nicht lösbar ist.
Es sei G ³ und es gelte n = 1 und N = 3. $integral F (y) = || \~/ u||2 dx G$

$1-- 1- Y = C (G), D = {y (- C (g)| y(x) = g(x), x (- @G}, y|@G = g$
Es sei y und v Y . Dann ist y + v genau dann, wenn v ₀ mit ₀ = {y C¹(G)|y|_G = 0}.
$integral @F(y;v) = 2 \~/ y(x)\ ~/ v(x)dx G$

$integral [ ] F (y + v)- F(y) = || \~/ ||2 + 2 \~/ y . \~/ v + || \~/ v||2 - || \~/ y||2 dx = G integral = || \~/ v ||2dx + dF(y,v) > dF(y;v) A v (- D0 G$ (4.2)

Gleichheit gilt genau dann, wenn v = const. mit v ₀. Da an den Rändern v = 0 gilt, ist v = 0 überall erfüllt. F(y) ist damit auf strikt konvex. Nach Satz 1 müssen wir nun y₀ aus F(y₀;v) bestimmen:
$integral dF(y ;v) = 2 \~/ y (x) . \~/ v(x)dx = 0 A v (- D 0 0 0 G$
Falls es ein y₀ C²(G) $/~\$ C¹(G) mit $/_\$ y₀(x) = 0 für x G (y₀ ) und y₀(x) = g(x) für x G, dann gilt F(y) > F(y₀) y mit yy₀.

Beweis:

Es sei v ₀:
$integral \~/ y0 . \~/ v dx G$
Es gilt nach HMII:
$\~/ .(v \~/ y0) = \~/ v . \~/ y0 + v /_\ y0$
Damit folgt nach dem GAUßschen Satz:
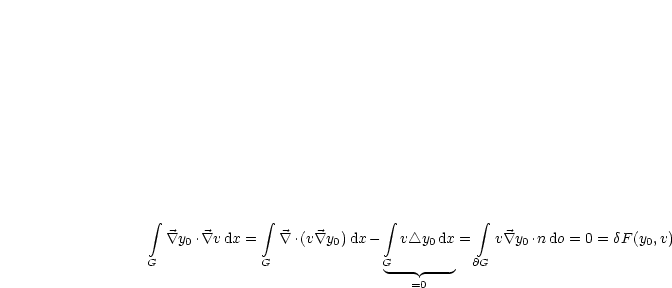
$integral integral integral integral \~/ y0. \~/ v dx = \~/ .(v \~/ y0) dx- v /_\ y0 dx= v \~/ y0 .n do = 0 = dF(y0,v) G G G--- --- @G =0$
Der vorletzte Schritt folgt dadurch, daß auf dem Rand v = 0 ist.

Wir behandeln im folgenden eindimensionale Probleme:

integral b F (y) = f(x,y(x),y'(x))dx a

In Integranden haben wir eine Funktion f = f(x,z,p) mit x [a,b] und (z,p) D ² (Gebiet). Außerdem setzen wir voraus, daß f_z und f_p stetig ist, daß also f_z, f_p C([a,b] × ).

Da,b = {y (- C1[a,b],(y(x),y'(x)) (- D,0 < x < b}

Die Funktionen, welche bei b willkürlich sind, aber bei a vorgeschrieben wird, liegen in ^b:

b a,b D = {y (- D | y(a) = a1}

Die Funktionen, welche sowohl bei a als auch bei b vorgeschrieben sind, liegen in :

D = {y (- Db|y(b) = b} 1

Und natürlich benötigen wir noch:

D0 = {y (- C1[a,b]| y(a) = y(b) = 0}

Man erkennt, daß ^b ^a,b und ₀ ^a,b.

Definition:

|----------------------------------------------------------------------------------------|
| |
|f = f(x,z,p) heißt [stark] konvex bez¨uglich z, p (f bei festgehaltenem x bez¨uglich z, p konvex ist),
|falls f(x,z +f, p+ y)- f(x,z,p) > fz(x,z,p)f+ fp(x,z,p)y A (x,z+ f,p+ y), (x,z,p) (- [a,b]× D =: S|
|gilt. Gleichheit gilt nur, falls f .y = 0 gilt. |
-----------------------------------------------------------------------------------------

Beispiel:

Es sei f(x,z,p) = p². Dann gilt f_z = 0 und f_p = 2p.

2 2 2 f(x,z+ f,p+ y)- f(x,z,p) = (p+ y) - p = 2py + y > fp(x,z,p).y+ 0.f

Gleichheit gilt nur im Falle = 0. Daher gilt auch für beliebiges , daß ^. = 0 ist; es liegt also starke Konvexität vor.

Beispiel:

Betrachten wir:

u = f(x,z,p) = xp + z, fp = x, fz = 1

Hierbei handelt es sich um eine Ebene im (u,z,p)-Raum.

f(x,z+ f,p+ y)- f(x,z,p) = x(p+ y)+ z+ f- xp -z = xy +f = fpy +fzf

Wir haben immer das Gleichheitszeichen, womit die Funktion konvex, aber nicht stark konvex ist.

Lemma:

|----------------------------------------------------------------------------------------|
| a,b |
|f sei bez¨uglich z, p [stark] konvex. Dann gilt F (y + v)- F(y) > dF (y;v) A y, y + v (- D . [Gleichheit
|gilt nur, falls v(x) = const.f¨ur a < x < b.] |
-----------------------------------------------------------------------------------------

Beweis:

f(x,y(x)+v(x),y'(x)+v'(x))- f(x,y(x),y'(x)) > fz(x,y,y')v(x)+fp(x,y,y')v'(x)

[Gleichheit gilt, falls v(x) ^. v'(x) = 0 ist, also v(x) = const..] Wir integrieren dieses Beziehung von a bis b:

integral b integral b f(x,y(x)+v(x),y'(x)+v'(x))-f(x,y(x),y'(x)) > fz(x,y,y')v(x)+fp(x,y,y')v'(x) a a

F-(y-+-v)--F(y) >-dF-(y;v)| -------------------------

Satz 2:

Beweis:

Es gilt nach dem vorhergehenden Lemma:

F (y + v)- F(y) > dF (y;v) A y (- Db und v (- C1[a,b] mit v(a) = 0

[Gleichheit gilt für v(x) = const. = 0, da nach Vorgabe v(a) = 0 ist.] Da ^b haben wir die strikte Konvexität auch auf ^b.

integral b F(y+v)- F(y) > dF (y;v) = [fz(x,y(x),y'(x))v(x)+ fp(x,y(x),y'(x))v'(x)] dx a

Satz 3:

|----------------------------------------------------------------------------------------|
| d |
|Gilt fu¨r y0 (- Da,b--fp(x,y0(x),y'0(x)) = fz(x,y0(x),y'0(x)) (EULER -Gleichung E) f¨ur a < x < b, so |
|folgt: dx |
| |
|dF(y0;v) = fp(b,y0(b),y'0(b))v(b) -fp(a,y0(a),y'0(a))v(a) A v mit y0 + v (- Da,b. |
| |
-----------------------------------------------------------------------------------------

Beweis:

integral b dF(y;v) = [fz(x,y0(x),y'0(x))v(x) +fp(x,y0(x),y'0(x))v'(x)] dx = a integral b[ ] integral b = d-fp(x,y0,y')v(x) +fp(x,y0(x),y'(x))v'(x) dx = -dfp(x,y0(x),y'(x))v(x) dx 0 0 dx 0 a a

(4.3)

Satz 4:

|----------------------------------------------------------------------------------------|
| |
|Es sei f bez¨uglich z, p [stark] konvex auf [a,b]× D (1) und y0 (- Da,b gen¨uge der Gleichung (E) (2). Dann
|minimiert y0 das Funktional F |
| |
| i.) [eindeutig] auf D, falls y0 (- D |
| ii.) [eindeutig] auf Db, falls y (- Db und f(b,y (b),y'(b)) = 0 |
| 0 p 0 0 |
| iii.) [eindeutig bis auf Konstanten] auf Da,b, falls fp(b,y0(b),y'0(b)) = fp(a,y0(a),y'0(a)) = 0 |
-----------------------------------------------------------------------------------------|

Beweis:

(1) ist die Voraussetzung von Satz 2 und (2) die Voraussetzung von Satz 3.

Aus Satz 2 folgt, daß F auf [strikt] konvex ist. F(y₀;v) wird für alle v ₀ nach Satz 3 gleich Null. Satz 1 liefert dann die Behauptung.
F ist auf ^b [strikt] konvex nach Satz 2. v für F(y₀;v) bedeutet v(a) = 0. Nach Satz 1 muß ein Minimum die Gleichung F(y₀;v) = 0 v mit v(a) = 0 erfüllen. Hieraus folgt dann f_p(b,y₀(b),y₀'(b)) = 0.
Wir wissen, daß nach dem Lemma gilt F(y + v) - F(y) > F(y₀;v) [Gleichheit, falls v = const.]. Nach Satz 1 gilt F(y;v) = 0, falls f_p(a,y₀(a),y₀'(a)) = f_p(b,y₀(b),y₀'(b)) = 0 ist nach Satz 3.

Zu ii.), iii.) und Satz 4:

Probleme, bei denen auf dem Rand nicht vorgegeben ist, bezeichnet man als Probleme mit freien Randwerten.

Die bei der Minimierung von F auf ^b bzw ^a,b zusätzlich auftretenden Randbedingungen heißen die zugehörigen natürlichen Randbedingungen.

Zur EULER-Gleichung (E):

Ist f C²[a,b] × D, so lautet (E) ausführlich:

fpx(x,y0,y')+ fpz(x,y0,y')y' +fpp(x,y0,y')y''= fz(x,y0(x),y'(x)) 0 0 0 0 0 0

Es handelt sich um ein Randwertproblem für eine nichtlineare Differentialgleichung 2.Ordnung für y₀.

Wir betrachten nun den Satz 4 für Spezialfälle:

Funktion f hängt nicht von z ab: f = f(x,p)
Hier sei das Problem der Brachystochrone angegeben. Wir suchen die kürzeste Laufzeit:
$integral x1 V~ -------- T(y) = V~ 1- 1+-y'(x)2-dx 2g x x=0$
Funktion f hängt nicht von x und z ab: f = f(p)
Ein Beispiel hierfür ist die kürzeste Verbindung zwischen zwei Punkten:
$b integral V~ ----'2--- L(y) = 1 + y (x)dx a$

$y(a) = a1 und y(b) = b1$

Corollar 1:

|----------------------------------------------------------------------------------------|
|Es sei f = f(x,p) bez¨uglich p auf [a,b]× I [stark] konvex und |
| |
| i.) D = {y (- C2[a,b]| y(a) = a1,y(b) = b1}, y'(x) (- I f¨ur a < x < b |
| |
|dann gilt: |
| integral b ' |
|Jedes y0 (- D mit fp(x,y'0(x)) = const.fu¨r a < x < b minimiert F(y) = f(x,y(x))dx [eindeutig] auf
| a |
|der Menge D. |
| ii.) Db = {y (- C1[a,b]| y(a) = a ,y'(x) (- I (a < x < b)} |
| 1 |
|dann gilt: |
|Jedes y0 (- Db mit fp(x,y'0(x)) = const. f¨ur a < x < b und fp(b,y'0(b)) = 0 (nat¨urliche Randbedingung)
| integral b |
|minimiert F(y) = f(x,y'(x))dx eindeutig auf Db. |
| a |
| |
-----------------------------------------------------------------------------------------

Beweis von i.):

ist eine Teilmenge von ^a,b womit wir Satz 4 anwenden können. Betrachten wir die EULERsche Differentialgleichung:

d ' dxfp(x,y0(x)) = 0

Dies gilt, da f nicht von y(x) abhängig ist.

Beweis von ii.):

Es ist f_p(x,y₀'(x)) = 0 für a < x < b und y₀(a) = a₁ zu erfüllen.

Corollar 2:

|----------------------------------------------------------------------------------------|
| |
| b1--a1 |
|EsseiD wieobenund f = f(p)aufI [stark]konvexund m = b -a . Dann isty0(x) = m(x -a)+a1 (- D
| integral b |
|die [eindeutig festgelegte] Minimalfunktion f¨ur F(y) = f(y'(x))dx auf D. |
| a |
-----------------------------------------------------------------------------------------

Beispiel:

Wir haben folgendes Funktional:

integral 2 F(y) = 1y'(x)2dx auf D = {y (- C1[1,2]| y(1) = 0,y(2) = 3} 1 x

Als Übung kann gezeigt werden, daß f stark konvex ist. Damit ist das Integral strikt konvex und wir können die EULER-Gleichung verwenden. Nach Corollar 1 [Teil i.)] gilt dann:

fp(x,y'(x)) = 2y'(x) = C1 x

' y (x) = Cx

Durch Integration folgt:

1 2 y(x) = 2Cx + C2

Mittels der Randbedingungen y(1) = 0 und y(2) = 3 können wir C und C₂ berechnen:

1 0 = -C + C2 2

3 = 2C + C2

|-------2----| -y(x) =-x---1|

Betrachten wir nur die erste Randbedingung, also ^b = {y C¹[1,2]|y(1) = 0}, so gilt nach Corollar 2 [Teil ii.)]:

2- ' x y(x) = 0, y(1) = 0

Damit erhalten wir schließlich x:

|--------| |y(x) = 0| ---------

Betrachten wir das Problem schließlich noch auf ^a,b = {y C¹[a,b]}, so folgt x:

|--------| -y(x) =-C|

Beispiel:

Die Länge einer Kurve berechnet sich nach:

integral b F(y) = V~ 1-+-y'(x)2dx a

Fall 1: : ₍a,a₁), (b,b₁) $d y'(x) dx- V~ ----'2---= 0 1+ y (x)$
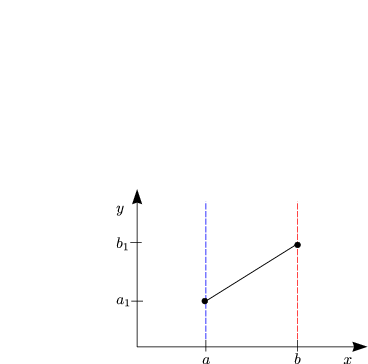
Daraus folgt y'(x) = const.
Fall 2: ^b : (a,a₁)
Es gilt y'(x) = const. und außerdem:
$' fp(y'(b)) = 0 = V~ -y-(b)-- 1 + y'(b)$
Damit ergibt sich y'(b) = 0 und somit auch y'(x) = 0, womit y(x) = const. = ₁ ist.
Fall 3: ^a,b
Aus y'(x) = const., y'(b) = y'(a) = 0 folgt y(x) = C mit C .

[next] [prev] [prev-tail] [front] [up]

Kapitel 4Konvexe Funktionale

Definition:

Satz 1:

Beweis:

Beispiel:

Beweis:

Definition:

Beispiel:

Beispiel:

Lemma:

Beweis:

Satz 2:

Beweis:

Satz 3:

Beweis:

Satz 4:

Beweis:

Zu ii.), iii.) und Satz 4:

Zur EULER-Gleichung (E):

Corollar 1:

Beweis von i.):

Beweis von ii.):

Corollar 2:

Beispiel:

Beispiel:

Kapitel 4
Konvexe Funktionale