3 Die Variation eines Funktionals

[next] [prev] [prev-tail] [tail] [up]

Kapitel 3
Die Variation eines Funktionals

Es sei Y ein Vektorraum mit

Y und F: D

sei ein Funktional. Es sei y₀

₀ und v

Y mit:

Es gibt ein > 0, so daß .

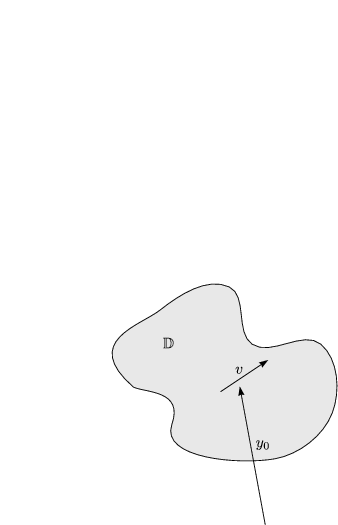
Wir betrachten jetzt () = F(y₀ + v) mit : [-₀,₀] und ₀ < < ₀. Wir definieren nun '(0) = F(y₀;b). Diese heißt 1.Variation von F in y₀ in Richtung v (1. GATEAUX-Ableitung von F in y₀ in Richtung v).

3.1 Plateau-Problem
3.2 Konvexität

Ausführliche Formulierung:

1 1 dF(y0;v) = lim -(f(f)- f(0)) = lim- (F(y0 + ev)- F(y0)) e'-->0 e e0 e

Hierbei handelt es sich gerade um die Definition der Richtungsableitung aus HMII. Beispiele hierfür sind:

f''(0) = d2F(y0;v)

Dieses wird als 2. Variation bezeichnet.

f: ⁿ ist ein Funktional mit Y = = ⁿ. $df(y0;v) = Dvf (y0) = \~/ f (y0).v$
f: , () = f(y + v) $|-'---------------'------| -f(0) =-df(y0,v) =-f-(y0).v$
sei zweimal differenzierbar:
$' ' '' '' 2 f (e) = f (y0 + ev)v, f (e) = f (y0 + ev) .v$
Damit gilt:
$|--------------------------| f''(0) = d2f(y0;v) = f''(y0).v2 ----------------------------$

Wir wollen nun f(y₀ + v) in eine Taylor-Reihe entwickeln:

f(y0+ev) = f(y0)+f '(y0).ev+ 1f''(y0).e2v2+O(e2) = f (y0)+edf(y0;v)+ 1e2d2f(y0;v)+O(e2) 2 2

Die Verallgemeinerung ist:

|------------------------------------------------| |F(y0 + ev) = F (y0)+ edF (y0,v)+ 1e2d2F(y0,v)+ O(e2) ------------------------------2-------------------

1 fxi = leim'-->0e [f (x1,x2,...,xi + e,xi+1,...,xn)- f(x1,...,xn)] mit (x1,x2,...,xi+e, xi+1,...,xn) = x+eei

dF(y;v) = lim 1[F(y+ ev)- F (y)] e'-->0 e

Definition:

|----------------------------------------------------------------------------------------|
| |
|D heiß t offen, wenn es zu jedem y (- D auch ein e > 0 gibt mit folgender Eigenschaft: |
| |
|{z|||z -y|| < e}< D |
-----------------------------------------------------------------------------------------

Wir wollen an dieser Stelle den Begriff „Norm“ zu wiederholen. Man kann eine Norm auf verschiedene Art und Weise definieren:

V~ ---- V~ -2---2----2 ||x ||= x.x = x1 + x2 +x 3

||x|| = max(|xj| ,j = 1, 2, 3)

Die Eigenschaften der Norm sind:

||||> 0 (= 0 = )
|||| = ||||||
|| + ||<|||| + ||||

Es sei I = [a,b] und G ein Intervall. Dann definieren wir folgende Norm:

|--------------------------| |||x||^C1(I) = max (|y(x)|,| y'(x)|) ---------------------------

Nun wieder zurück zur Variation.

f(e) = F (y0 + ev)

f'(0) = dF (y0;v)

f''(0) = d2F(y0;v)

Wir wollen die Funktion () entwickeln:

1 f(e) = f(0)+ ef'(0)+ 2e2f''(0)+ O(e2), e '--> 0

Analog kann man dies für Variationen definieren:

F(y0 + ev) = F (y0)+ edF (y0;v)+ 1e2d2F(y0;v)+ O(e2), e '--> 0 2

Lemma 1:

|----------------------------------------------------------------------------------------|
| |
|Y sei Vektorraum, D < Y und F, G: D '--> R seien Funktionale, fu¨r welche die dF (y;v) und dG(y;v)
|existieren, wobei y (- D, v (- Y fest sind. Dann gelten: |
| • d(F + G)(y;v) = dF (y;v)+ dG(y;v) |
| |
| • d(cF )(y;v) = cdF(y;v) f¨ur c (- R |
| Die in y in Richtung v GATEAUX -differenzierbaren Funktionale bilden einen reellen Vektorraum
| bez¨uglich der¨ ublichen Operationen bei Funktionen. |
| |
| • dF (y;cv) = cdF (y;v) f¨ur c (- R |
| |
| • dF (y;-v) = - dF(y;v) |
-----------------------------------------------------------------------------------------

Wir wollen die beiden letzten Eigenschaften beweisen:

Fall c = 0: $dF (y;0) = 0$

$1 dF(y;0) = lim-[F(y +e .0)- F(y)] = 0 e'-->0 e$
Fall c0: $dF (y;cv) = lim 1 [F (y + ecv) - F(y)] = c.lim 1(F(y +jv) - F(y)) = cdF(y,v) mit j = ce e'-->0 e j'-->0 j$

Lemma 2:

|----------------------------------------------------------------------------------------|
| |
|y, v (- [D, Y mit e, j seien derartig, daß die im folgenden auftretenden Grenzwerte existieren alle|
|existieren: |
| d || |
| 1.) dF(y+ jv;v) = deF(y+ ev)|| |
| e=j |
| 2.) d2F (y;cv) = c2d2F(y;v) mit c (- R |
| |
-----------------------------------------------------------------------------------------

Wir beweisen die erste Aussage:

1 1 ' ' dF(y+jv;v) = lie'-->m0 e [F (y + jv+ ev)- F(y + jv)] = eli'-->m0 e [f(e+ j)- f(j)] = f (j) = f (e)|e=j

Nun bleibt noch die zweite:

d2F (y;v) = f''(0) = lim 1 [f'(e)- f'(0)] = lim 1 [dF (y+ ev;v)- dF(y;v)] e'-->0 e e'-->0e

Bezeichnungen/Abkürzungen:

integral F(y) = f(x,y(x),Dy(x))dx mit x (- Rn, y(x) (- RN und G (_ RN (N = 1, 2, 3) G

(y1(x1,x2,...,xN)) y2(x1,x2,...,xN) y(x) = .. . yn(x1,...,xN )

Alle möglichen partiellen Ableitungen 1.Ordnung aller Koordinatenfunktionen nennen wir (Dy_i(x)).

( ) nN Dy(x) = D1y1(x),...,D1yn(x),D2y(x),...,D2yn(x),D3y1(x),...,D3yn(x), ...,DN-y1(x),...,DN-yn(x) ( - R D1y(x) D2y(x) D3y(x) DNy(x)

f : U < RN × Rn × RnN

f = f(x,z,p)

\~/ zf = (fz1,...,fzn) = fz

\~/ pf = (fp1,...,fpnN) = fp

Behandeln wir zwei Spezialfälle, die sehr häufig auftreten:

n = 1:
y ist eine skalare Funktion und Dy(x) ist der Gradient von y.
N = 1:
Es handelt sich um eine Raumkurve. Dy(x) ist die Tangente an die Raumkurve.

dF (y;v) = ?

integral f(e) = F (y+ ev) = f (x;y(x)+ ev(x),y'(x)+ ev'(x))dx G

integral d integral f'(e) = --f(x,y(x)+ev(x),Dy(x)+Dev(x)) dx = [fz .v(x,y+ ev,Dy + Dev)+ fp .Dv(x, y+ ev,Dy + eDv)] dx G de G

integral f'(0) = dF (y,v) = [fz .v(x,y(x),Dy(x)) + fp .Dv(x,y(x),Dy(x))] dx G

Man kann dies auch in Koordinatendarstellung schreiben:

sum n fz .v = fzj .vj j=1

Schauen wir uns hierzu einige Beispiele an:

integral 1 ' F (y) = ||y (x)||dx N = 1, z = n, p = (p1,p2,...,pn) = n 0

Da wir nur eine Variable haben gilt:

Dy = (y'1(x),y'2(x),...,y'n(x))

V~ --------------- f(x,z,p) = p21 + p22 + ...+ p2n

' fz = 0, fp = (fp1,...,fpn) =-p-, fp(x,y(x),Dy(x)) =-y(x)- ||p|| ||y'(x)||

|------------------------| | integral 1 ' ' | |dF(y;v) = y-(x)'.v(x)dx | | 0 ||y (x)|| | --------------------------

Durch partielle Integration folgt:

|-------------------------------------------| | |1 integral 1 [ ] | dF (y;v) = y'(x)-.v(x)|| - v(x) -d--y'(x)-- dx | | ||y'(x)|| |0 dx ||y'(x)|| | -----------------------0---------------------

integral [ ] dF(y;v) = fz(x,y(x),Dy(x)).v(x)+ fp(x,y(x),Dy(x)) .Dv(x) dx G (- Rn (- RnN

Schauen wir uns dazu noch einige Spezialfälle an:

n = 1, N = 1: $|------------------------| | integral b | F (y) = f(x,y(x),y'(x))dx | -------a------------------$
n = 1, N: $|----------------------------------| | integral N | |F(y) = f (x,y(x), \~/ y(x))dx, G (_ R| -------G---------------------------$
n, N = 1: $|------------------------| | integral b | |F(y) = f (x,(x),y'(x))dx | | a | -------------------------$