3.2 Konvexitt

[prev] [prev-tail] [tail] [up]

3.2 Konvexität

Auf dem ersten Übungsblatt hatten wir gezeigt:

f(t1x1 + t2x2) < t1f(x1)+ t2f(x2)

Es sei hier z₁, t₂ [0,1] x₁, x₂ I und t₁ + t₂ = 1.

Definition:

|----------------------------------------------------------------------------------------|
| N |
|Eine Menge G < R '--> R heiß t konvex, falls f(t1x1+ t2x2) < t1f(x1) +t2f(x2) A t1, t2 wie oben und A
|x1, x2 (- G gilt, falls G selbst konvex ist. |
-----------------------------------------------------------------------------------------

\text{[math]}

Ist f C¹(I), dann gilt: f ist konvex auf I genau dann, wenn die Ableitung f' monoton wachsend ist. Daraus folgt:

' f (x) - f(x0) > f(x0)(x - x0) A x, x0 (- I

Definition:

$|----------------------------------------------------------------------------------------| | | |f: G (_ RN '--> R heiß t konvex auf G, falls f (- C1(G) und f(x) -f(x0) > \~/ f (x0).(x - x0) A x, x0 (- G |beziehungsweise f(x+ v)- f(x) > \~/ f (x).v. | | | -----------------------------------------------------------------------------------------$

Beispiel:

Es sei folgende Funktion gegeben:

f(x) = ||x||2 f¨ur x (- Rn

Unser Ziel ist, folgendes zu zeigen:

\~/ f (x0).(x - x0) < f(x)- f(x0)

Der Gradient unserer Funktion ist:

\~/ f(x) = 2x

Also muß gelten:

2 2 2x0 .(x - x0) < ||x|| - ||x0||

Durch Umformen folgt nun mit der Schwarzschen Ungleichung:

2 2 2a.b < 2|| a||||b|| < ||a|| + ||b||

2x .x- 2||x ||2 < ||x ||2 + ||x||2- 2||x ||2 0 0 0 0

Beispiel:

f(x) = ||x ||f¨ur x (- Rn

\~/ f (x) .v < f(x +v) -f (x) = ||x+ v||- ||x||

Für den Gradienten gilt:

\~/ f (x) =-x- ||x||

x .v x.(x + v) ||x||||x+ v|| \~/ f (x) .v =-||x|| =---||x||---- ||x||< ---||x||-----||x|| = f(x+ v - f(x)

Der letzte Schritt folgt aus der Cauchy-Schwarzschen-Ungleichung.

Beispiel:

V~ ---------- g(x,y) = 1 + x2 + y2(= f(1,x,y))

Wir schauen uns dazu ganz allgemein folgendes Funktion an:

V~ -------- x g(x) = 1+ ||x||2 f¨ur x (- Rn, \~/ g(x) =--- g(x)

\~/ g(x) .v < g(x +v) -g(x)

Aussage 1:
Es sei f: G ⁿ ein Gebiet. f sei auf G konvex und besitze in x₀ G eine stationäre Stelle (das heißt mit $\~/$ f(x₀) = ). Dann wird f in x₀ minimal.
Aussage 2:
Ist f auf G strikt konvex, so besitzt f höchstens einen stationären Punkt x₀ in G.
Beweis:

Wir nehmen an, daß x₀, x₁ mit x₀x₁ stationäre Punkte sind. Dann gilt:
$f (x) > f(x0) f¨ur x /= x0$

$f (x) > f(x1) f¨ur x /= x1$
Die erste Beziehung gilt für alle x, also insbesondere auch für x₁. Die zweite Ungleichung gilt natürlich auch für x₀, womit also folgt:
$f(x1) > f(x0) und f(x0) > f(x1)$
Dies stellt ein Widerspruch dar, womit die Aussage bewiesen ist.
Beispiel:
- f(x) = ||x||² ist strikt konvex auf ⁿ.
- f(x) = ||x|| ist konvex auf ⁿ \{0}.
  Dies kann man zeigen durch:
  $\~/ f (x).v = x.v-< ||x +v|| - ||x|| ||x||$
Beispiel:

Zu zeigen ist, daß g(x) strikt konvex auf ⁿ ist:
$V~ ------2- g(x) = 1+ ||x||$
Wir verwenden obige Funktion f(y) = ||y|| mit y ⁿ⁺¹. Dann ist g(x) = f(1,x) mit x ⁿ.
$g(x+v) -g(x) = f(1,x+v)- f(1,x) = f((1,x)+(0,v))-f(1,x) > \~/ f (1,x).(0,v)$

$y (1,x) \~/ f(y) =---, \~/ f (1,x) = V~ -----2- ||y|| 1+ ||x||$
Wir multiplizieren skalar mit (0,v):
$\~/ f (1,x).(0,v) = ( V~ 1,x).(0,v)-= V~ -x.v---= \~/ g(x).v 1 + ||x||2 1+ ||x||2$
Das Gleichheitszeichen gilt für:
$( 1) (0) (1) x + v || x$

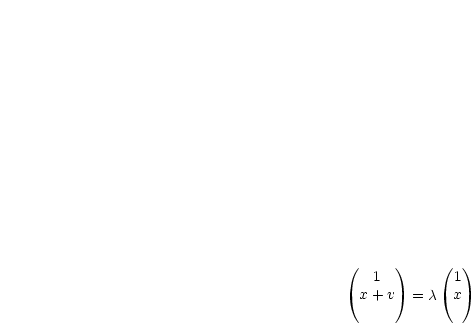
$( 1 ) ( 1) x +v = c x$
Für = 1 gilt x + v = x und damit v = 0, womit dies gezeigt ist.

Übung:

Es ist zu zeigen, daß $\~/$ g(x) ^. v < g(x + v) - g(x) ist.

[prev] [prev-tail] [front] [up]