5.1 Geodtische Linien

Wir wollen nun diese Linien auf einem geraden Kreiszylinder betrachten.

0 < f2 < p

Wir suchen die Kurve in Parameterdarstellung, wobei wir r = 1 setzen:

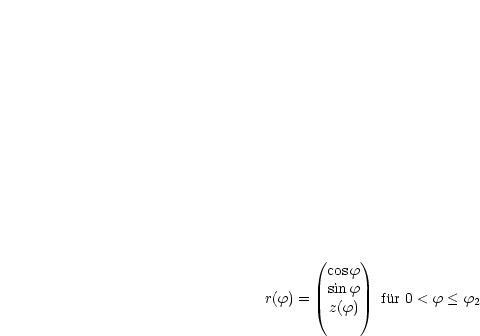
( ) cosf sin f r(f) = z(f) f¨ur 0 < f < f2

Es gilt z(0) = z₁) und z(₂) = z₂. Gesucht ist z₀ = {z C¹[0,₂]|z(0) = z₁, z(₂) = z₂} mit:

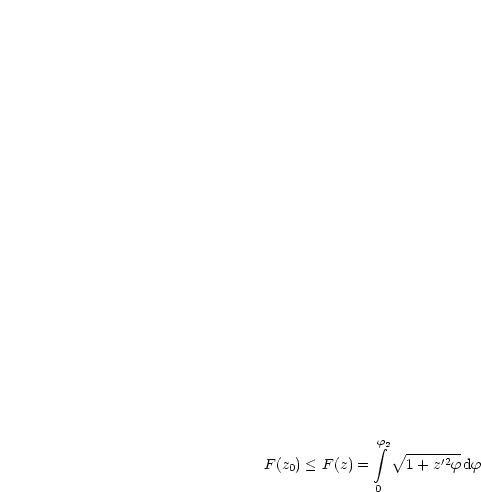
f2 integral V~ ---'2- F(z0) < F (z) = 1+ z f df 0

Mit unseren Bezeichnungen können wir schreiben f(p) = . Wir wissen, daß strikte Konvexität vorliegt. Damit folgt nach Corollar 2:

|-------z---z--------| |z(f) = 2---1-.f +z1 | ---------f2----------|

Damit gilt also:

|-----(-----------)---------------| | cos(f) | r(f) = z2-sizn1(f) f¨ur 0 < f < f2| | f2 f+ z1 | -----------------------------------