5.2 Brachystochrone

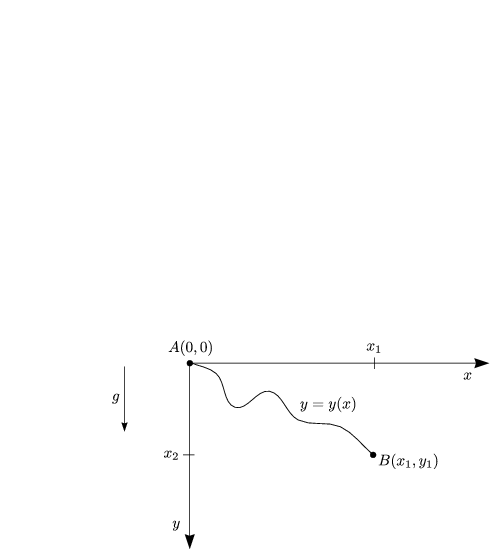
Das zu untersuchende Funktional lautet:

integral ds x integral 1 V~ 1-+-y'2(x) T (y) = v(y) = - V~ --------dx 0 2gy(x)

Zu untersuchen ist ein Variationsintegral mit dem Integranden:

V~ ------ f(x,z,p) = 1+-p2- z

Diese Funktion ist jedoch nicht konvex. Deshalb betrachten wir dasselbe Problem, aber wir vertauschen die Achsen.

Dann sieht unser Integral folgendermaßen aus:

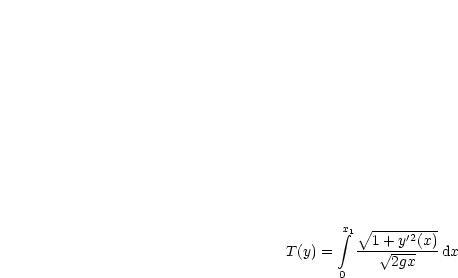
integral x1 V~ 1-+-y'2(x) T(y) = -- V~ ------dx 0 2gx

Dieses Funktional ist also zu minimieren aus = {y C¹[a,b]|y(0) = 0,y(x₁) = y₁}. Bei diesem Vorgehen können jedoch gewisse Kurven verloren gehen.

V~ ------ f(x,z,p) = V~ 1 1+ p2 x

Da dieser Ausdruck stark konvex ist, ist T(y) strikt konvex auf und wir können den Satz 1 anwenden:

d-- ' ' dxfp(x,y(x),y(x)) = fz(x,y(x),y (x))

Diese Differentialgleichung ist nun zu lösen.

' V~ 1- V~ -y-(x)--= 1, wobei C = const. x 1 + y'(x) C

Durch Auflösen nach y'(x) erhalten wir dann:

'2 --x--- 2 y (x) = C2- x f¨ur x < C

Wir lesen hier ab, daß y'(0) = 0 ist; also liegt im Ursprung eine waagerechte Tangente. Anstelle von x wird nun der Parameter (bei Zykloide: Rollwinkel) eingeführt.

C2 (h ) x(h) =-2-(1- cosh) = C2 sin2 2- , x(0) = 0

Damit dieses auch wirklich eine Parametertransformation ist, muß x() bijektiv sein. Bei Injektivität darf die Ableitung von x() nicht gleich Null sein:

C2- ˙x(f) = 2 sin h > 0 f¨ur 0 < h < p (f¨ur 0 < h < h1 < p)

x = x(): [0,₁][0,x₁] ist bijektiv, falls 0 < ₁ < . Wir schreiben nun y(x()) = (). Dann resultiert mit der Kettenregel:

˙y(h) = y'(x(h))x˙(h) = y'(x(h)).C2-sin h 2

4 C2 4 4 ˙y(h) = y'2(x(h)).C-sin2h = ---2-(12--cosh)-- .C--sin2h = C--(1- cosh)2 4 C2 - C2 (1 -cosh) 4 4

Wir ziehen die Wurzel:

|------C2----------| |˙y(h) =---(1 - cosh)| --------2-----------

Durch Integration folgt:

|--------2---------| |y(h) = C-(h - sin h)| --------2----------|

Damit haben wir eine Kurvendarstellung, welche durch A(0,0) geht.

C², ₁ sind so zu bestimmen, daß (x(), ()) durch B verläuft.

(x1,y1) = (x(h1),y(h1))

Zerlegen wir die Parameterdarstellung der Zykloide:

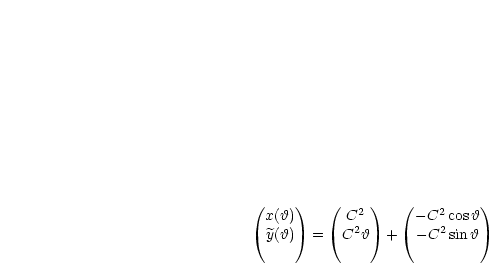
( ) ( ) ( ) x(h) C2 -C2 cosh y(h) = C2h + - C2sin h

Wir betrachten folgende Funktion:

h(h) = y(h)-= h---sinh-f¨ur h > 0 x(h) 1 - cosh

Berechnen wir den Grenzwert mittels der Taylorreihenentwicklung, so folgt:

h(0) = 0,hl'-->im2p h(h) = oo

Außerdem kann man nachprüfen, daß h'() > 0 ist für 0 < < 2. h() ist damit streng monoton wachsend auf [0,2] und h = [0,). Daraus folgt dann, daß es genau ein ₁ [0,2) mit h(₁) = . Es gilt damit: